d라이브러리

미국 수학 잡지인 ‘월간 미국 수학’에는 독자가 만든 문제를 엄선해 소개하는 코너가 있습니다. 이중에 몇몇 문제는 수학 연구로 발전해 계속해서 연구되고 있습니다. 이번 호에 소개할 문제 역시 1967년에 독자가 만든 문제와 관련이 깊습니다. 

KAIST 수리과학과 건물 1층에는 수학도서관이 있습니다. 제가 대학생이던 20여 년 전에도 있었으니 제법 오래된 도서관입니다. 사실 1990년대 초만 해도 우리나라 도서관에서 볼 수 있는 른 나라 학술지는 많지 않았습니다. 수학 연구를 하다 보면 몇십 년 지난 논문을 봐야 할 때도 많은데, 당시에는 인터넷도 발전하지 않아 오래된 논문을 보는 게 쉽지 않았죠. 

그런데 이 도서관에는 1890년대에 출판된 학술지까지 모두 구비돼 있어 다른 대학에서 이 도서관으로 편지를 보내 논문을 부탁하고 복사된 논문을 받아봤습니다. 학교 역사가 짧은데 어떻게 이런 게 가능한지 당시에는 마냥 신기하기만 했습니다. 알고 보니 학교 초창기에 교수님들 연구비를 각출해 학술지부터 갖췄다고 하더군요.

1990년대 초 대학원생도 아니었던 제가 전문가들이 보는 수학 학술지를 읽었던 것은 아닙니다. 다행히 그곳에는 학부생도 취미로 읽을 만한 수학 잡지가 몇 개 있었습니다. 특히 미국수학협회에서 나오는 수학 잡지 3개, ‘월간 미국 수학(The American Mathematical Monthly)’, ‘수학 잡지(Mathematics Magazine)’, ‘대학 수학 잡지’(The College Mathematics Journal)’를 많이 봤습니다.

여기에는 대학생이 배울만한 수학 정리를 새롭게 증명하는 법처럼 사소해 보이지만 흥미로운 연구가 실려 최근 호가 아니더라도 재미있게 볼 수 있었습니다. 사소해 보인다고 연구 내용을 무시해서는 안 됩니다. 여기 실린 연구로 미국 수학자이자 경제학자인 로이드 섀플리 교수는 2012년 노벨경제학상을 받았으니까요.

제가 이 잡지들을 즐겨본 이유가 하나 더 있습니다. 이 세 잡지에는 모두 수학 문제 코너가 있습니다. 독자들이 보내온 수학 문제를 선별해 싣는 코너입니다. 문제가 실린 뒤에는 한동안 답안을 모아서 그중 좋은 답안을 다시 실어줍니다. 풀이를 보내면 보낸 사람의 이름을 실어주는데, 저도 한 번 이름이 나간 적이 있었습니다. 이름 순서를 잘못 적어서 이름과 성이 거꾸로 나가 아쉬웠지만요. 저뿐만 아니라 이 코너에 열심히 참여한 우리나라 분들이 있었습니다. 

독자가 만든 문제, 수학 연구로!

이번 호에 소개할 문제는 ‘월간 미국 수학’ 1967년 3월호 고급 문제 코너에 실린 문제로, 미국 뉴멕시코주립대학교 소속이던 프레드 리치맨과 존 토마스가 만든 겁니다.

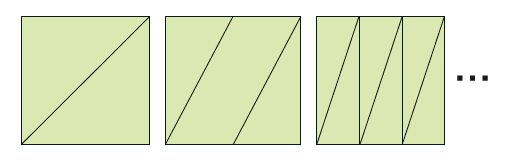
N이 짝수라면 얼마든지 가능합니다. 이 글을 보는 수학동아 독자라면 금방 위 그림을 떠올렸을 겁니다.

하지만 N이 홀수라면 어떻게 될까요? 물론 N=1일 때 불가능하다는 것은 누구나 쉽게 알 수 있습니다. 그렇다면 모든 홀수에 대해 이런 방법으로 쪼개는 것이 불가능할까요? ‘월간 미국 수학’ 1968년 11월호에는 이 문제의 풀이가 실릴 차례였지만, 아무도 푼 사람이 없어 나가지 못했습니다. 이보다 앞서 ‘수학 잡지’ 1968년 9월호에 토마스가 쓴 4쪽짜리 짧은 논문에 이 문제의 일부를 해결한 내용이 담겼다는 안내만 실렸죠. 

토마스의 논문에 따르면 리치맨은 1960년대 중반부터 주변 수학자들에게 이 문제를 묻고 다녔고, N=3이나 N=5일 때는 불가능하다는 것을 증명했다고 합니다. 이후 토마스는 만일 평면 위에서 네 점 (0,0), (1,0), (1,1), (0,1)을 잇는 정사각형을 분할하는 문제라고 하면, 각 삼각형의 꼭짓점의 좌표가 분자가 홀수 또는 0인 유리수로 나타나도록 분할하는 것은 불가능함을 보였습니다. 하지만 여전히 원하는 답은 아니었죠. 삼각형의 꼭짓점 좌표가 무리수거나 분자가 짝수일 때는 어떻게 되는지 전혀 알 수가 없었거든요.

아름다워 잊기 힘든 증명

그 해답은 1970년 미국 브랜다이스대학교 교수였던 폴 몬스키가 찾아냅니다. 몬스키는 모든 홀수 N에 대해 정사각형을 넓이가 서로 같은 삼각형 N개로 분할하는 것은 불가능하다는 사실을 멋지게 증명해 ‘월간 미국 수학’에 소개합니다. 이 증명은 매우 멋있고 아름다워서 한 번 보면 잊어버리기 쉽지 않습니다. 게다가 아직까지도 이 문제의 풀이는 이 몬스키의 방법 말고는 다른 방법이 없습니다.

증명이 어떻기에 아름답냐고요? 평면에 있는 모든 (x, y)를 세 가지 색 중 하나로 잘 칠합니다. 
그렇게 칠하고 난 뒤 한 변 길이가 1인 정사각형을 어떻게 삼각형으로 쪼개든 어떤 삼각형은 꼭짓점 3개의 색깔이 모두 다를 수밖에 없다는 것을 증명합니다. 그리고 꼭짓점 3개의 색깔이 모두 다르다면 그 삼각형의 넓이는 0도 아니고 홀수분의 1 꼴도 아니라는 것을 보입니다. 

평면에 있는 점의 색을 정할 때 좌표가 유리수이면 쉽게 색을 정할 수 있습니다. 하지만 좌표가 무리수일 때는 조금 더 어려운 이론을 사용합니다. 그런데 그런 어려운 이론을 쓰는 풀이만 있다고 하니 신기할 노릇이지요.

이 증명은 독일의 두 수학자 마틴 아이그너와 권터 지글러가 쓴 책 ‘하늘책의 증명(Proofs of THE BOOK)’에도 실렸습니다 . 여기서 ‘THE BOOK’이라고 하는 말은 유명한 헝가리 수학자 에르되시 팔이 자주 쓰던 말로, 신이 있다면 아마도 수학의 여러 정리의 완벽한 증명을 모아서 만들어 놓았을 책을 가리키는 표현입니다. 

이 책의 3판이 한국어로 번역돼 나왔는데 한글판 제목이 ‘하늘책의 증명’이어서 어떤 서점에서는 종교서적 코너에 책을 꽂아놓았더라는 말이 있을 정도로 홍보가 잘 되지 않아 아쉬운 책입니다. 아쉽게도 몬스키의 증명은 영문판 4판부터 들어갔기 때문에 당장 한국어로 이 부분을 접하기는 어려울 것 같습니다. 4판은 한국어 번역본이 나와 있지 않거든요.

삼각형끼리는 넓이가 얼마나 비슷할까? 

한편 지글러는 최근 재미있는 연구 결과를 학술지 ‘실험 수학(Experimental Mathematics)’에 발표했습니다. 독일 베를린 자유대학교의 장-필리프 라베 연구원, 귄트터 로테 교수와 함께 정사각형을 N이 홀수인 N개의 삼각형으로 쪼갤 때, 넓이가 서로 최대한 비슷하게 한다면 얼마나 비슷할 수 있을지 연구했습니다. 

만약 넓이가 1인 정사각형을 삼각형 N개로 쪼갰을 때, 각각의 넓이를 a1, a2, …, aN이라고 합시다. 

원래 문제는 a1=a2=…=aN이 되도록 쪼개는 것이지만, 이는 불가능하다는 것을 이미 몬스키가 밝혔습니다. 따라서 연구팀은 모든 i, j에 대해 |ai-aj|≤c가 되는 최소인 c값을 찾을 수 있을지 알아봤습니다. 그리고 그 값을 Δ(N)라고 할 때 다음 식이 성립한다는 것을 증명했지요.

오른쪽 부등식은 삼각형으로 잘 쪼개면 넓이 차이가 2-blog2N 이하가 되도록 쪼갤 수 있다는 뜻입니다. 그 전까지 가장 좋은 연구 결과는 2011년에 Δ(N)이 어떤 상수 d에 대해 d2N 이하라고 밝힌 건데, 이를 훨씬 개선한 겁니다. 왼쪽 부등식은 삼각형끼리 서로 넓이가 최대한 비슷하게 하려고 해도 2-2aN 이상 차이 나는 두 삼각형이 있다는 뜻입니다. 

여러분도 수학 문제를 만들고 푸는 즐거움을 느껴보면 어떨까요? 재미있는 수학 문제를 만들고 풀다보면 먼 훗날 그 문제 덕분에 새로운 수학 연구가 시작될 수도 있습니다.