d라이브러리

※ 김종락 서강대학교 수학과 교수는 포스텍 수학과를 졸업하고, 서울대학교에서 석사 학위, 미국 일리노이주립대학교 시카고캠퍼스에서 박사 학위를 받았습니다. 주요 연구 분야는 부호론과 암호론, 산업수학, 인공지능입니다. 2004년 캐나다 조합론연구소에서 주는 커크만 메달을 한국인 최초로 받았습니다. 2016년부터 대한수학회 수학문화 앰배서더로 활동 중이며, ‘감성수학레드’라는 스타트업을 운영하고 있습니다.

바둑판 위에 검은색, 흰색 바둑돌을 번갈아 가며 놓고, 같은 색 돌 다섯 개를 가로세로 또는 대각선 방향으로 나란히 놓으면 이기는 게임을 ‘오목’이라고 합니다.

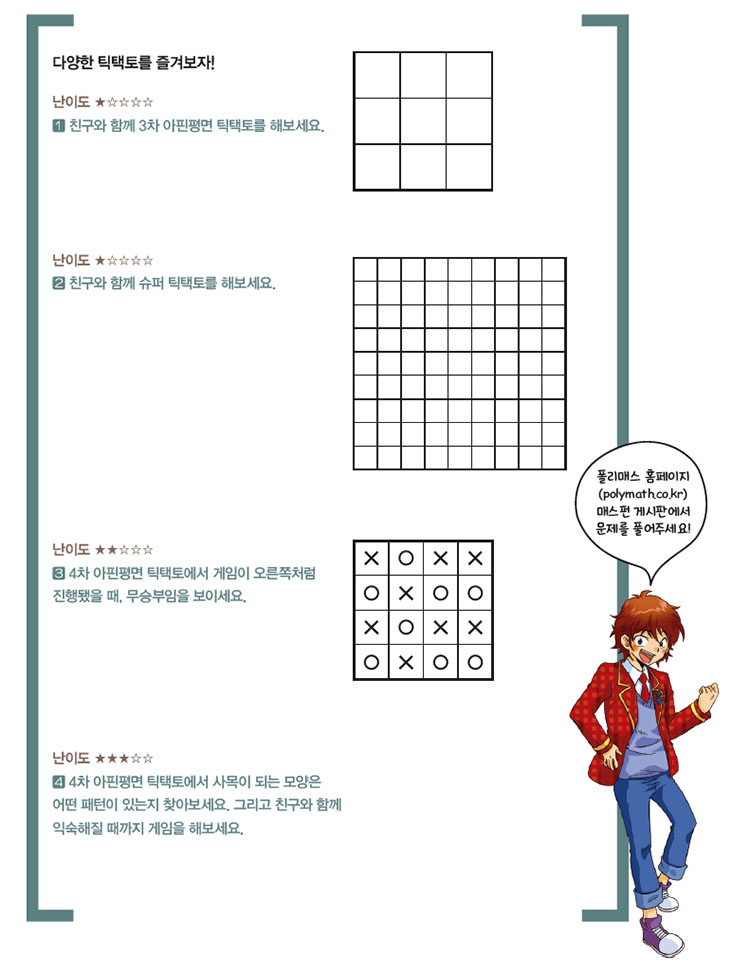
오늘 소개할 ‘틱택토’ 게임은 쉽게 말해 ‘삼목’이라고 할 수 있어요. 차이가 있다면 돌을 놓는 대신 3×3 게임판의 빈칸에 ◦, ×를 표시한다는 겁니다.

규칙이 간단한 건 장점이지만, 빈칸이 9개밖에 없고 오목과 다르게 ◦ 또는 ×를 세 개만 놓아도 이길 수 있어서 익숙해지면 무승부로 끝나는 경우가 많다는 게 단점입니다. 틱택토를 좀 더 재밌게 하는 방법은 없을까요?

끊겨도 괜찮다, 아핀평면 틱택토!

2006년 미국 스크랜턴대학교 수학과 교수였던 스티븐 도허티는 새로운 규칙을 추가한 ‘아핀평면 틱택토’를 소개했어요. 도허티 교수는 3×3 게임판을 그대로 사용하면서 삼목이 만들어지는 모양을 4개 추가했지요.

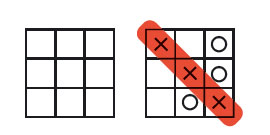
원래 틱택토에서는 삼목을 만들 수 있는 모양이 가로세로 각각 3개, 대각선 2개로 총 8개 있어요. 아핀평면 틱택토에서는 아래 왼쪽에 있는 네 가지 모양도 삼목으로 생각해서 삼목을 만들 수 있는 모양이 총 12개입니다.

×가 일렬로 놓여있지 않은데, 어떻게 삼목이냐고요? 아래 오른쪽 그림처럼 게임판을 복사해서 상하좌우에 붙였다고 생각해 보세요. 처음엔 엇갈려 있던 ×가 이어져 대각선 방향으로 삼목이 됩니다. 쉽게 떠올리기 어려우면 게임판의 가로 또는 세로줄 세 개를 다시 배치해서 대각선 방향으로 삼목이 되는 거라고 생각해도 됩니다.

아핀평면 틱택토는 일반적인 틱택토보다 삼목을 만들 수 있는 경우가 많기 때문에 그만큼 전략도 다양합니다. 더 심사숙고해서 ◦ 또는 ×를 표시해야겠죠?

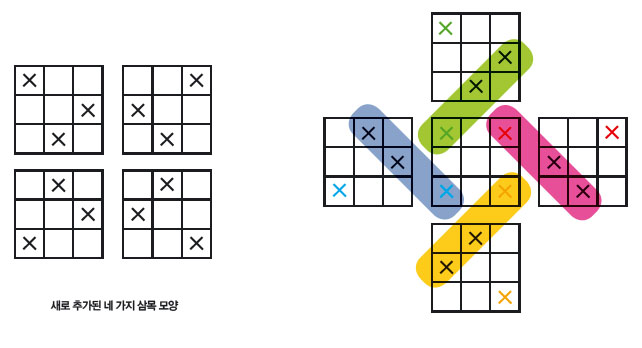
아핀평면 틱택토의 다른 이름은 ‘토러스 틱택토’입니다. ‘토러스’는 수영할 때 쓰는 튜브나 가운데 구멍이 하나 뚫린 도넛처럼 생긴 모양을 뜻해요.

토러스 틱택토라고 부르는 이유는 틱택토 게임판을 위 아래로 둥글게 말아 빨대처럼 만든 뒤 양 끝을 이어 붙이면 토러스가 되는데, 그러면 아핀평면 틱택토에서 새로 추가한 삼목 모양이 토러스 위에서 나란히 연결되기 때문이에요.

종이와 펜이 있으면 직접 만들어 확인해 볼 수도 있습니다. 좌우가 긴 직사각형 종이를 가로세로 삼등분해서 게임판을 그린 뒤, 새로 추가한 네 가지 삼목 모양 중 하나를 그려보세요.

이제 위아래 모서리를 붙여 빨대처럼 만들고 양 끝을 이어보세요. ×가 나란히 놓인 걸 확인할 수 있을 거예요.

무승부가 없는 아핀평면 틱택토

3×3 틱택토는 9칸을 모두 채워도 무승부인 경우가 많습니다. 하지만 아핀평면 틱택토는 절대 그렇지 않아요. 이유가 무엇일까요?

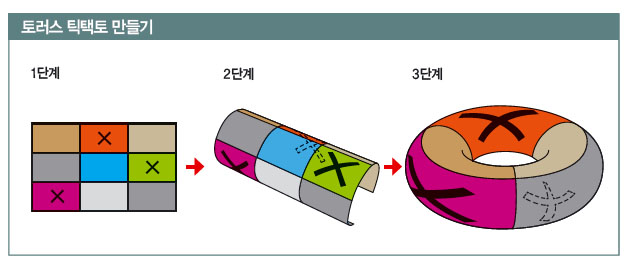
아핀평면 틱택토에서 빈칸을 ◦와 ×로 모두 채운 상태에서 무승부라고 가정해 볼게요. 게임을 먼저 시작한 사람이 ×를 표시한다고 가정하면, 게임판 위에 ×는 5개, ◦는 4개 있을 거예요. 이제 ×가 게임판 모서리에 4, 3, 2, 1개 있는 경우로 나눠 무승부가 나올 수 없다는 사실을 보이도록 하죠. 각 경우에 틱택토를 90°씩 돌려보면 147쪽 위에 있는 모양이 됩니다.

먼저 동서남북 4곳에 ×가 있다면, 즉, 147쪽 ❶번 그림처럼 회색으로 표시한 부분에 ×가 있어야 합니다. ×가 5개려면 ×를 하나 추가해야 합니다. 만약 ×를 한가운데 추가하면 삼목 2개가 만들어지고, 모퉁이 4곳 중 어디에 추가해도 아핀평면 틱택토에서 추가한 모양 중 하나가 되기 때문에 반드시 ×가 이길 수밖에 없지요.

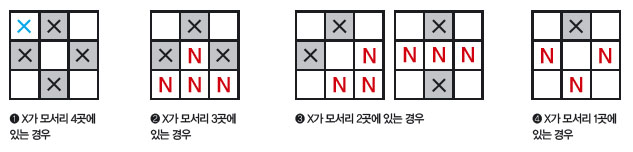
❷번 그림처럼 3곳에 ×가 있는 경우, ×를 두 개 추가해야 합니다. N으로 표시한 부분은 ×가 있으면 바로 삼목이 만들어지거나, ❶번과 같은 경우이기 때문에 추가하면 안 되는 칸이에요. 이제 남은 칸은 윗줄 좌우 모퉁이밖에 없는데, 여기에 ×를 표시하면 첫 번째 줄에 삼목이 만들어져 ×가 이깁니다.

모서리 2곳에 ×가 있는 경우는 ❸번 그림처럼 두 가지가 있어요. 빨간색 N은 앞의 경우와 마찬가지로 ×를 표시하면 안 되는 칸입니다. 이제 남은 빈칸에 × 3개를 추가하면 반드시 삼목이 만들어져 역시 ×가 이기게 되지요.

❹번 그림은 1곳에 ×가 있고, ×가 들어가면 안 되는 곳을 N으로 표시한 그림이에요. 이 경우 ×를 4개 추가해야 하는데, 한가운데 추가하면 나머지 4개가 모퉁이에 있어야 해서 반드시 대각선 방향으로 삼목이 생기고, 한가운데 ×가 없으면 네 모퉁이에 ×가 들어가야 하므로 맨 윗줄에 삼목이 생길 수밖에 없습니다.

n차 아핀평면 틱택토

n차 아핀평면은 특정 조건을 만족하는 점 n2개의 모임을 말해요. 특정 조건이란, 평면 위에 모든 직선★이 점 n개를 지나야 하고 이 직선들 중에 서로 공통된 점을 갖지 않는 직선이 n개 있어야 한다는 거예요. 이러한 직선을 ‘서로 평행하다’ 또는 ‘n2개의 점을 분할했다’고 해요. 예를 들어, 아래 그림에서 색이 같은 직선은 모두 서로 평행해요.

직선★ n차 아핀평면에서 직선은 ‘모양이 상관없는 점 n개의 모임’으로, 곡선도 직선으로 생각한다.

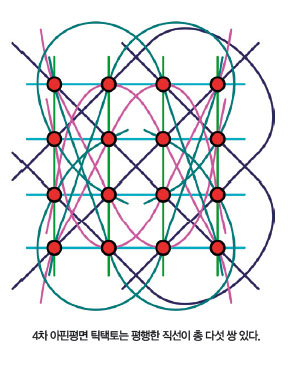
앞에서 소개한 틱택토는 새로 추가한 삼목 모양 중 2개를 지나는 선분과 대각선 중 하나가 모여 이 조건을 만족하니까 3차 아핀평면 틱택토지요. 즉, n차 아핀평면 틱택토는 평행한 직선이 지나는 점을 n목으로 생각하는 틱택토인 셈입니다. 3차 아핀평면 틱택토처럼 게임판을 상하좌우로 붙인다고 점들이 항상 나란히 놓이는 건 아니니 주의해야 해요!

틱택토 속에 틱택토가? 슈퍼 틱택토!

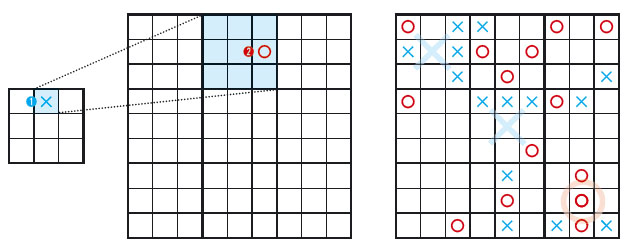
이제 틱택토 계의 끝판왕, ‘슈퍼 틱택토’를 소개할 차례예요. ‘최상의 틱택토’라고도 부르는 슈퍼 틱택토는 게임판 크기가 크게 보면 3×3인데, 각 칸에는 또다시 3×3 게임판이 있어서 사실상 9×9인 셈입니다.

규칙은 이렇습니다. 9개의 3×3 틱택토 중의 하나를 선택해 빈칸 중 한 곳에 ◦ 또는 ×를 표시합니다. 만약 위에 왼쪽 그림처럼 한가운데 있는 틱택토의 윗줄 가운데 ×를 표시하면(❶), 다음 사람은 윗줄 가운데 있는 틱택토로 가서 빈칸 중 한 곳에 ◦를 표시합니다(❷).

이제 ×를 표시하는 사람은 큰 틱택토 게임판에서 ◦가 표시한 위치에 해당하는 틱택토로 가서 ×를 표시하면서 게임을 진행합니다. 만약 게임이 무승부로 끝나면 아무것도 적지 않고, 그게 아니면 이긴 사람의 기호(◦ 또는 ×)를 작은 틱택토 위에 크게 적습니다. 큰 틱택토에서 승부가 난 곳을 제외한 다른 틱택토의 빈칸에 ◦ 또는 ×를 표시해야 합니다. 결국 큰 틱택토에서 먼저 삼목을 만드는 사람이 최종 승자가 됩니다.

슈퍼 틱택토에서 항상 이길 수 있는 전략은 아직 모릅니다. 2013년 이스라엘 히브리대학교 컴퓨터공학과 박사과정생이었던 에이탄 리프쉬츠와 데이비드 츄렐은 컴퓨터 시뮬레이션을 이용해 슈퍼 틱택토를 통계적으로 분석한 결과, 먼저 하는 사람이 이길 확률이 56%라는 사실을 밝혔어요.

먼저 하는 사람이 나중에 하는 사람보다 이길 확률이 조금 높지만, 열심히 하면 6% 정도는 얼마든지 뒤집을 수 있지 않을까요?