d라이브러리

시험이 끝났어요! 끝나지 않을 것 같던 고통스러운 한 주였습니다. 우리는 준우네 집에서 신나게 놀며 시험에서 받았던 스트레스를 날려버리기로 했어요. 시험으로 잠시 막아놨던 에너지를 한창 분출하다 보니 배가 출출해졌습니다. 우리는 언제나 옳은 치킨을 시키기로 했습니다. 그런데… 문제가 생겼어요!

우리는 심각한 고민에 빠졌습니다. 5명일 때 치킨을 몇 마리 시켜야 할까요? 직접 맞닥뜨려보면 알겠지만, 생각보다 골치 아픈 문제입니다.

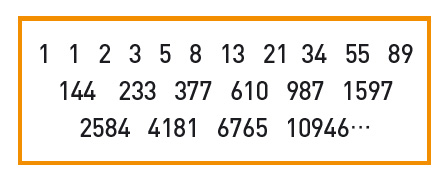
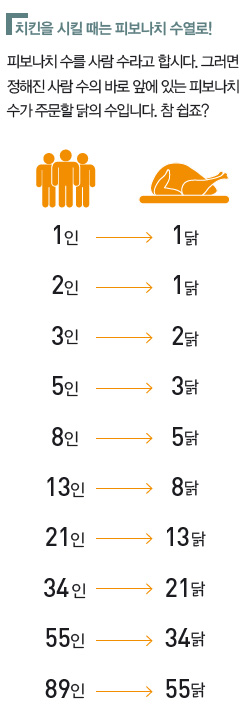
그런데 정체를 알 수 없는 서울대학교 학생이 이 문제를 명쾌하게 풀어 놓은 게 아니겠어요?! 바로 ‘피보나치 수열’을 이용하는 겁니다. 피보나치 수열은 1과 1로 시작하고, 앞의 두 수의 합이 바로 뒤의 수가 되는 수열입니다. 피보나치 수열을 나열하면 아래와 같습니다. 아래 수를 ‘피보나치 수’라고 합니다.

주문 전화를 하려던 찰나 준우네 옆집 사는 친구 동석이가 나타났습니다. 귀신 같은 녀석…. 치킨을 시키기도 전에 냄새를 맡은 것 같군요. 결국 우리는 6명이 먹을 치킨을 시키기로 했습니다. 아뿔싸! 피보나치 수에는 6이 없는데 어쩌죠?

제켄도르프 양념 추가!

피보나치 수열에는 없는 자연수가 많아 이런 문제가 생겼어요. 다행히 서울대 학생이 이 문제도 풀어놓았더군요! 이름도 낯선 제켄도르프 정리를 이용해서요. 제켄도르프 정리에 따르면 피보나치 수를 활용해서 모든 자연수를 나타낼 수 있어요.

제켄도르프 정리

모든 자연수는 하나 이상의 연속하지 않는
피보나치 수의 합으로 나타낼 수 있고, 이는
유일하다.

제켄도르프 정리를 이해하기 위해 예를 하나 들어볼게요. 100을 피보나치 수로 분해한다고 해봐요. 그러면 100=89+8+3, 100=89+8+2+1, 100=55+34+8+3 같은 방법이 있어요. 하지만 이중 100=89+8+3만 제켄도르프 정리를 따릅니다.

100=89+8+2+1은 1과 2가 연속하는 피보나치 수고, 100=55+34+8+3은 34와 55가 연속하는 피보나치 수이기 때문이에요.

우리는 6명이 먹을 치킨이 몇 마리인지 알기 위해서 먼저 제켄도르프 정리에 따라 6을 5+1로 분해했어요. 5명일 때 3마리, 1명일 때 1마리를 시키면 되니, 6명일 때는 총 4마리를 시키면 됩니다.