d라이브러리

매년 어린이날마다 ‘OO월드 실시간’, ‘OO랜드 오늘 인파’를 검색
하며 눈치싸움을 벌여야 했던 놀이공원 방문! 올해는 코로나19 때문에 가기 힘들 것 같아서 직접 만들어보려고 합니다. 
꿈과 희망이 가득한 퓨처랜드를 제작해봅시다!

※ 편집자 주
LOL, 오버워치, 배그부터 다양한 인디게임까지 섭렵한 게임 인생 6년차 퓨처킴. 하지만 마인크래프트(이하 마크)는 처음 이다. 회사에서 게임하는 게 조금 눈치 보이지만 마크 초고수가 되는 그날까지, 나는 달린다!

▲ PDF에서 고화질로 확인할 수 있습니다.

전화 통신에서 시작한 대기행렬이론

 
자! 퓨처랜드 간판까지 만들고 나니 진짜 테마파크 같죠? 그런데 특정 놀이기구에만 손님이 몰려서 줄이 길어질까 걱정됩니다. 롤러코스터나 바이킹 같은 재밌는 놀이기구에는 줄이 엄청 길잖아요. 만약 롤러코스터를 타는 데에 평균 3시간을 기다려야 한다면, 그냥 가는 사람도 있을 거예요. 그렇다고 탑승 인원을 무리하게 늘리면 안전 문제가 생길 수 있죠. 그래서 오늘은 기다림을 수학적으로 분석하는 ‘대기행렬이론’을 이용해 놀이기구 대기시간을 줄이는 법을 알아보겠습니다.

요즘은 전화하고 싶은 사람에게 전화를 걸면 바로 통화가 되지만, 20세기 초에는 송신자와 수신자를 전화 교환원이 연결해줘야 했어요. 통화량이 많을 때는 전화 교환원이 연결해줄 때까지 한참을 기다려야 통화할 수 있었죠. 이런 불편함을 해결하기 위해 덴마크의 수학자 ‘아그너 얼랑’은 기다림 없이 대부분의 전화 통화를 연결하는 데에 필요한 최소 전화 교환원이 몇 명인지 알기 위해 연구했습니다. 그렇게 시작한 이론이 대기행렬이론이죠. 현재서비스를 받기 위해 대기해야 하는 분야에서 다양하게 쓰이고 있습니다.

예측을 도와주는 확률 분포

대기행렬 모형을 만들 때 중요한 사항은 ‘일정 시간 동안 고객의 방문 횟수’와 ‘서비스 제공 시간이 얼마나 걸리는지’입니다. 이것을 예측할 수 있어야 대기행렬을 줄일 방법을 고민할 수 있기 때문이죠. 그런데 고객의 방문 횟수나 서비스 제공 시간은 상황에 따라 조금씩 달라지기 때문에 딱 잘라 답할 수 없습니다. 이럴 때 ‘확률 분포’를 이용하면 대략적으로 예측할 수 있죠.

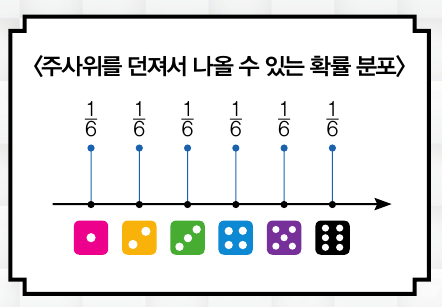
주사위를 던져서 나올 수 있는 수의 확률 분포를 구하려 하면, 먼저 주사위를 던져서 나올 수 있는 수를 먼저 확인해야 합니다. 정육면체 주사위를 던져서 나올 수 있는 수는 1, 2, 3, 4, 5, 6인데, 이를 ‘확률 변수’라 하죠. 확률 분포는 확률 변수가 특정 값을 가질 확률을 나타내는 분포를 말해요. 

대기행렬이론에선 일정한 시간 동안 발생하는 사건의 횟수를 예측할 수 있는 ‘푸아송 분포’와 다음 사건이 일어날 때까지 대기 시간을 예측할 수 있는 ‘지수 분포’가 주로 쓰입니다. 놀이기구 상황을 예로들면 푸아송 분포는 일정 시간 동안 특정 놀이기구를 방문하는 고객의 수를, 지수 분포는 놀이기구의 운행 시간을 예측합니다. 

기다림을 재미로 바꾸는 다양한 서비스

사실 놀이기구의 대기행렬 모형을 만들기 위해선 놀이기구를 타고 떠나는 사람의 수보다 놀이기구를 타려고 오는 사람의 수가 더 적어야 한다는 전제가 필요해요.

하지만 나들이 철 인기 놀이기구에는 타려는 사람이 더 많기 때문에 대기행렬 모형을 적용할 수 없죠. 그래서 대부분의 놀이공원은 다른 서비스를 제공해 대기 시간이 지루하지 않게 만들어요. 
예를 들어 줄을 서는 동안 군것질을 할 수 있도록 대기 장소 근처에 스낵 코너를 배치하거나, 사진을 찍을 예쁜 장소를 만들어 놓습니다.

 여러분이 가장 좋아하는 놀이기구는 어떤 건가요? 좋아하는 놀이기구를 퓨처킴처럼 실제로 작동하도록 만들어보세요!