d라이브러리

확률 분야의 떠오르는 샛별은 2010년 필즈상을 받은 스타니슬라프 스미르노프 교수의 제자 휴고 듀밀-코핀 교수입니다. 박사 과정 때인 2012년 가장 권위 있는 학술지인 ‘수학연보’에 연구를 발표하며 수학계에 눈도장을 확실히 찍었습니다. 이 연구는 지금까지도 대단한 업적으로 평가받고 있습니다.

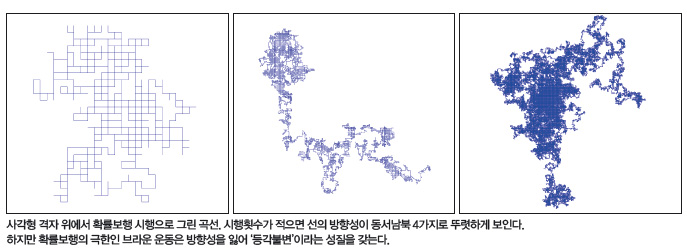
육각형 격자를 따라 선을 긋는 시행을 n번 합니다. 한 점에서는 세 방향으로 선분을 그을 수 있으니, 각 시행마다 무작위로 한 방향을 정해 선분을 긋는 게 됩니다. 매번 어느 방향으로 갈지 종잡을 수 없는 그림이 나오겠지요? 이처럼 불규칙하게 움직이는 모습을 설명하는 확률 모델을 ‘확률보행’라 부릅니다. 기체나 액체 속의 작은 입자가 불규칙하게 움직이는 현상을 나타내는 브라운 운동을 설명할 때 주로 쓰이지요.

듀밀-코핀 교수는 무작위로 그린 선 중에서 자기 자신과 만나지 않는 선만 주목해 살펴봤습니다. 이를 ‘자기회피산책로(SAW)’라 하는데, n이 커질때 원점에서 출발한 이러한 선의 개수가 어떤 속도로 늘어나는지 알아본 겁니다. 그 결과 기하급수적으로 증가한다는 기존의 추측을 해결했지요. 듀밀-코핀 교수가 지수함수의 밑, 즉 an에서 a값이 

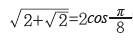
라고 정확하게 구한 겁니다. 또 이 곡선은 SLE( 8/3 )에 수렴한다고 추측했습니다. 여기서 SLE(k)는 속력이 k인 브라운 운동을 운동 함수로 갖는 뢰브너 방정식으로부터 얻은 확률곡선으로, ‘슈람 뢰브너 전개’라고 부릅니다.

SLE라는 필즈메달 텃밭에서 성과

어떤 곡선이 등각불변을 만족해야지만 SLE(k)로 표현이 가능한데요, 등각불변이면 물리현상을 이해하는 데 중요한 여러 구체적인 등식을 얻을 수 있기 때문에 수학은 물론 물리학에서까지 각광을 받습니다.

듀밀-코핀 교수는 2014년 ‘이징 모형’ 위에 그린 경계 곡선이 SLE(3)이 된다는 것도 증명했습니다. 금속 원자는 초소형 자석처럼 자성을 갖는데, 이 성질을 수학적으로 모형화한 것이 이징 모형입니다. 모형이 간단한데다 정확한 해를 구할 수 있어 고체 물리학에서 매우 중요하지요.

이런 뛰어난 성과에도 불구하고 듀밀-코핀 교수의 이번 필즈상 수상에 대해서는 반신반의하는 분위기입니다. 가장 큰 업적으로 평가받는 두 업적 뒤에 지도 교수가 있어서지요. 만약 이 모든 걸혼자 했다면 필즈상 수상이 유력하지만, 이미 대가로 평가받는 스미르노프 교수와 함께 했다고 하니 필즈상을 받기에는 아직 부족하다는 겁니다. 강남규 고등과학원 교수는 “듀밀-코핀 교수가 만약 40세 이전에 2012년 연구에서 추측한 내용을 혼자 증명한다면 필즈상 0순위가 될 것”이라고 말했습니다.

앞서 2018 필즈상 후보로 세드리크 빌라니 교수의 제자 알레시오 피갈리 교수(2018 수학동아 3월호)를 소개했었는데요, 피갈리 교수 역시 이번에 필즈상을 받기에는 몇 퍼센트 부족하다는 평가를 받는다고 전했었습니다. 그런데 듀밀-코핀 교수와 피갈리 교수 사이에 공통점이 또 있습니다. 지도 교수가 모두 2010년 필즈상 수상자라는 겁니다.

공교롭게도 빌라니 교수와 스미르노프 교수는 2022년 세계수학자대회를 유치하기 위해 각각 프랑스와 러시아 유치위원으로 활동하며 선의의 경쟁을 펼치고 있습니다. 이 결정 역시 2018 브라질 세계수학자대회에서 나옵니다. 둘은 묘한 라이벌 구도를 이루고 있는데요. 앞으로 누가 웃게 될지 궁금합니다.