d라이브러리

어느새 네 번째 방송으로 찾아온 수학동아TV의 BJ맹추입니다! 오늘의 수학 개념은 복잡한 계산은 없지만, 기호가 많아서 골치 아픈 ‘집합’이에요. 처음엔 헷갈려도 계속 보면 금세 익숙해지니까 포기하지 말고 끝까지 시청 바랍니다! 자, 그럼 시작해 볼까요?

일단 모이기만 해!

책상에 10분만 앉아있어도 몸이 근질근질하던 학창시절. 교실에서 하는 수업보다 운동장에서 하는 체육 수업을 좋아했던 저는 ‘수업이 끝났으니 이제 집합하세요’라는 체육 선생님의 외침이 정말 싫었습니다. 그럴 때마다 ‘집합이란 말을 없애든가 해야지’라고 툴툴대곤 했는데, 웬걸. 글쎄 이 녀석이 수학책에도 나오지 뭐예요.

‘집합’이라…. 선생님이 학생을 모을 때 ‘집합~’ 이라고 하니까 뭔가를 ‘모은다’는 뜻인 것 같은데, 수학책에 나오니까 왠지 심오한 뜻이 있을 것 같죠? 사실 수학책에 나오는 집합이라고 해서 특별한 건 없습니다. 숫자나 알파벳 같은 원소를 모아두면 그냥 ‘집합’이라고 부르거든요.

뜻만큼 기호도 단순합니다. 만약 숫자 1, 2, 3, 4가 모인 집합을 만들고 싶으면 ‘{’와 ‘}’ 사이에 1, 2, 3, 4를 넣어 {1, 2, 3, 4}로 나타내면 됩니다. 너무 쉽다고요? 그런데 사실 이 방법으로 갖가지 모임을 나타내기엔 문제가 있어요. 눈치 빠른 독자는 이미 알아챘을지도?

모임을 ‘잘’ 나타내는 방법

여러분이 생각한 문제점은 뭔가요? 제가 생각한 문제점은 ‘엄청나게 많은 원소가 모인 집합은 어떻게 나타내냐’는 겁니다. 원소가 10개만 있어도 적기 귀찮은데 자연수 집합처럼 원소가 셀 수 없이 많으면 일일이 적는 게 사실 불가능하니까요.

방법은 생각보다 간단합니다. 원소를 직접 쓰기 어려우니 그냥 글로 써주는 겁니다. 예를 들어, 자연수 집합은 {, } 사이에 ‘자연수의 모임’이라고만 적어도 자연수가 뭔지 아는 사람은 ‘집합에 1, 2, 3, 4…가 모여 있구나!’라는 사실을 알 수 있을 거예요. 이렇게 글로 설명하는 방법을 ‘조건 제시법’, 아까처럼 직접 쓰는 방법을 ‘원소나열법’이라고 불러요.

한 가지 주의사항! 조건제시법의 조건을 쓸 때는 반드시 ‘명확’하게 적어야 합니다. 다시 말하면, 누가 읽어도 똑같은 집합을 떠올려야 한다는 뜻이지요.

친구들에게 ‘적당~히 큰 자연수의 모임’을 집합 기호로 적으라고 하고 한번 살펴보세요. 어떤 친구는 100보다 큰 자연수를 쓰고, 1억쯤 돼야 크다고 생각하는 친구는 1억보다 큰 수를 쓸 겁니다. 영어처럼 집합 기호도 전 세계 사람이 공통으로 쓰는 거니까 누가 봐도 똑같은 집합을 떠올리도록 명확하게 적어야 합니다!

집합의 멋짐을 모르는 당신이 불쌍해

‘그런데 집합이 왜 필요해요?’라는 질문이 쇄도하네요! 이해합니다. 계산과 증명으로 가득한 수학에 집합은 필요 없어 보이겠지요. 집합이 필요한 이유는 집합을 이용하면 수학 개념을 아주 간단하게 나타낼 수 있기 때문이에요.

예를 들면, 저번 방송에 등장한 ‘함수’에서 관계있는 두 모임을 집합으로 표시하면 ‘이 모임에는 아메리카노, 카푸치노…가 있어요’라고 구구절절 설명할 필요가 없죠. 심지어 그래프를 집합으로 나타내도 됩니다. 일차함수 y=x+1의 그래프가 직선이고, 직선은 점의 모임이니까 조건제시법을 이용해 다음과 같이 조건을 나타낼 수 있습니다.

이렇게 집합은 수학 개념을 간단하게 나타내 주기 때문에 ‘수학의 언어’라고 해요. 집합이 얼마나 편리했던지, 칸토어를 비난하던 사람도 나중에는 집합을 잘~ 써먹었다는 사실!

#집합 더하기 집합은? #페르마 코스프레

어려서부터 수학에 사로잡힌 우리는 눈앞에 숫자 2개가 있으면 본능적으로 크기를 비교하거나 사칙연산을 하고 싶은 욕망이 샘솟습니다.

이 방송이 끝나면 여러분은 집합을 봐도 비슷한 욕망이 생길 겁니다. 집합도 수와 마찬가지로 사칙연산 비스름한 걸 할 수 있으니까요. 다만 집합은 수가 아닌 ‘모임’이기 때문에 조금 차이가 있죠.

수에 대소 관계가 있다면 집합에는 포함 관계(A⊂B)가 있습니다. 이 기호는 집합 B가 집합 A를 포함한다는 뜻으로, A에 있는 모든 원소를 B도 가지고 있음을 나타내지요. 간혹 포크 같은 기호(∈)도 볼 수 있는데, 이건 집합과 원소 사이의 포함 관계를 나타내는 기호니까 헷갈리지 마세요.

포함 관계 외에도 집합의 덧셈이라고 할 수 있는 합집합, 뺄셈과 비슷한 차집합, 그리고 교집합이나 여집합 같은 연산도 있습니다. BJ맹추는 아주 잘 알고 있지만, 하나하나 설명하기엔 여백이 모자라니 궁금한 사람은 오른쪽 그림을 참고 하시길!

벤이-그린-집합-그림, 벤 다이어그램!

소설보다 만화책이 읽기 쉬운 이유는 바로 그림이 있기 때문이죠. 함수는 그래프가 있으니 됐고, 집합은 그림으로 나타낼 수 없을까요? 물론 있지요. ‘벤 다이어그램’을 이용하면 집합을 그림으로 나타낼 수 있어요.

사실 가장 먼저 집합을 그림으로 나타낸 사람은 스위스 수학자 레온하르트 오일러인데, 1880년 영국의 논리학자 존 벤이 고안한 그림이 더 간편하고 편리해서 벤의 그림, 벤 다이어그램을 쓰고 있어요.

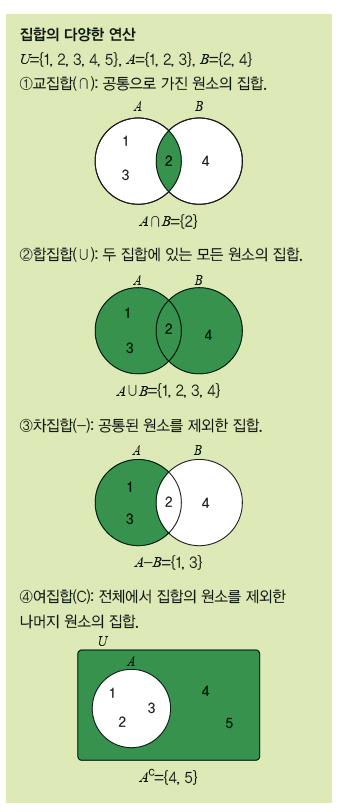
집합의 원소를 {, } 대신 원 안에 적고, 두 집합이 공통으로 가진 원소가 있으면 두 원을 겹쳐서 생긴 영역에 공통 원소를 적으면 됩니다. 위에서 집합의 연산을 설명할 때 나온 그림이 바로 벤다이어그램입니다!

칸토어가 비난 받은 이유, 무한집합!

방송을 마무리하기 전에 칸토어가 집합과 함수를 이용해 ‘무한’을 어떻게 정의했는지 쬐~끔 맛만 보도록 하죠.

칸토어는 어떤 집합과 그 집합의 진부분집합 사이에 일대일대응이 있으면 ‘무한집합’이라고 정의했어요. 진부분집합은 어떤 집합의 원소 일부를 뽑아서 만든 집합으로, 짝수인 자연수 집합은 자연수 집합의 진부분집합이지요. 이제 자연수 집합의 원소에 2를 곱해서 나온수를 짝수 집합에 있는 원소에 대응시켜 보세요. 1은 2, 2는 4, 3은 6…. 이처럼 자연수 집합의 원소 하나당 짝수 집합의 원소가 하나씩 대응하니까 자연수 집합은 무한집합인 겁니다. 

흥미로운 사실은 무한집합인 유리수 집합과자연수 집합 사이에도 일대일대응이 있다는 거예요. 두 집합의 원소를 하나씩 대응시키는 방법은…. 숙제! 오늘 밤 잠들기 전에 곰곰이 생각해 보세요!