d라이브러리

이번엔 어제 얘기예요. 가족이 이사를 하면서 오빠와 제 방을 정해야 했죠. 그런데 오빠가 큰 방과 작은 방을 보더니 당연하다는 듯 큰 방에 들어가서 눌러앉는 거예요. 1년 먼저 태어난 게 벼슬인가. 용돈도 많이 받으면서 큰 방까지 가지려 하다니! 저도 오빠에게 무조건 작은 방에 가라고 하는 게 아니에요. 오빠도 인간이면 합리적으로 나눌 방도를 찾자고요!

방을 나누는 건 어려운 문제지. 다행인 건 부모님이 “어떻게 하든 누군가는 불만을 가질 테니 네가 참아”라고 말한다면 이 말은 틀렸다는 거야. 수학자 프란시스 수가 모두가 만족할 방법이 있다는 걸 증명했거든. 물론 수는 남매가 아니라 룸메이트끼리 월세 나누는 방법을 다뤘지만, 너희도 용돈이나 가구를 나누면 되니까 수의 제안을 살펴보자.

월세 문제는 단순한 나눗셈으로 풀 수 없어. 어떤 사람은 햇빛을, 어떤 사람은 넓은 걸 좋아해서 사람마다 각 방에 매기는 가치가 다르거든. 수는 사람들의 취향과 월세 분배 방식을 도형 하나에 나타내기로 했어. ‘단체’에 관한 ‘슈페르너의 보조 정리’를 이용했지. 단체란 선분과 삼각형, 사면체처럼 N차원 도형이면서 꼭짓점이 N+1개인 것을 말해.

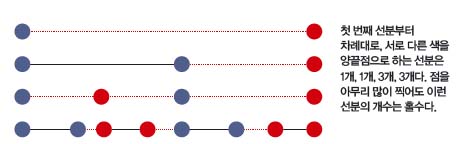
슈페르너의 보조 정리를 알기 위해 선분의 사례를 보자. 양 끝점의 색깔이 파랑과 빨강인 선분을 그려. 이때 선분 안에 빨간 점과 파란 점을 어떻게 찍든 서로 다른 색을 양 끝점으로 하는 선분은 하나 이상 존재해. 왜 그런지 알아보자.

처음엔 빨강과 파랑을 양 끝점으로 하는 선분이 1개야. 두 색깔 사이에 파란 점이나 빨간 점을 찍어도 여전히 1개지. 즉, 서로 다른 색깔 사이에 점을 찍을 땐 우리가 찾는 선분의 개수가 변하지 않아. 같은 색깔 사이는 어떨까? 파란색 사이에 파란 점을 찍으면 우리가 찾는 선분의 수가 그대로지만, 빨간 점을 찍으면 2개가 더 생겨. 따라서 우리가 찾는 선분은 처음엔 1개고 그다음엔 개수가 유지되거나 2개씩 더 늘어나므로 1, 3, 5, 7,… 로 항상 1개 이상이야.

슈페르너의 보조 정리는 모든 단체가 이런 성질을 갖는다는 거야. 예를 들어 꼭짓점의 색깔이 빨강, 파랑, 노랑인 큰 삼각형을 여러 작은 삼각형으로 쪼갠 뒤 작은 삼각형의 꼭짓점을 색칠한다고 하자. 이때 큰 삼각형의 세 변 위에 있는 점은 변의 양 끝점 중 하나와 같은 색으로 칠하고, 큰 삼각형 안에 있는 점은 빨강, 파랑, 노랑 중 하나를 칠해. 그러면 꼭짓점 색깔이 모두 다른 작은 삼각형이 적어도 하나 있어. 수는 이런 정리를 어떻게 월세 문제로 바꿨을까?

2명이 살면 선분, 3명이 살면 삼각형

위와 같이 수가 세운 가정 아래서 월세의 합이 100만 원인 빨간 방과 파란 방을 동생과 오빠가 나눈다고 하자. 선분을 하나 그리고, 양 끝점에 오빠와 동생을 각각 배정해. 이때 선분 위의 각 점(x1, x2)는 월세를 나누는 방식으로, x1는 빨간 방 월세고 x2는 파란 방 월세야. 그림➊처럼 가장 왼쪽 점은 (0, 100), 오른쪽 점은 (100, 0)이라고 하자.
 

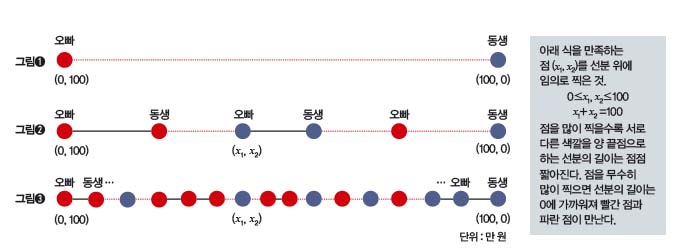
이제 각 점에 배정된 사람이 좋아할 방의 색깔로 점을 칠해. 왼쪽 점에 있는 오빠는 빨간 방을 좋아할 거야. 월세가 공짜니까. 오른쪽 점의 동생은 파란 방을 고르겠지. 선분의 꼭짓점 색이 다르다는 슈페르너의 가정을 만족했어.

다음으로 그림➋처럼 선분 안에 점을 찍고 두 사람을 번갈아 배정하자. 모든 점마다 동생 혹은
오빠에게 어떤 방이 좋은지 물어보고 원하는 방 색깔로 칠해. 슈페르너에 의하면 서로 다른 색깔
을 양 끝점으로 하는 선분은 적어도 하나 있어.

같은 방법으로 점을 늘려가면 그런 선분이 짧아지다 빨간 점과 파란 점이 한 점, 즉 같은 월세 분배 방식으로 모일 거야. 그때가 바로 오빠와 동생이 동시에 다른 방을 좋아하면서 월세에 만족하는 경우야. 꼭짓점 색깔이 다른 선분은 반드시 있으니까 모두가 만족하는 해법도 존재해.

수는 N명이 N개 방을 나눌 때는 N차원 단체로 나타낼 수 있다고 했어. 3명은 삼각형, 4명은 사면체로 말야. 몇 명이 방을 나누든 모두가 만족할 분배법은 항상 존재하는 거지.

이제 협상을 시작하지!

이번엔 게임이론★을 바탕으로 직접 협상을 해보자. 그러려면 각자가 생각하는 방의 가치를 알아야 해. 오빠는 큰 방을 가질 수만 있다면 동생에게 10만 원을 줄 수 있고, 동생은 큰 방을 가지면 오빠에게 5만 원을 줄 수 있다고 가정하자.

게임이론★ 자신의 이익을 달성하려는 사람들이 어떻게 의사 결정을 할지 연구하는 이론.

이때 방과 돈을 나누는 가장 쉬운 방법은 ‘분할선택법’이야. 한 사람이 분배 방법을 제시하면 상대방이 방을 고르면 돼. 방법을 제시하는 사람은 상대방이 너무 좋은 쪽을 고르지 않도록 최대한 공평한 방법을 생각해내겠지. 각자의 역할은 동전를 던져서 무작위로 정하면 돼.

그런데 문제가 있어. 분배 방법을 제시하는 사람에 따라 결과가 달라지거든. 돈의 최소 단위가 만 원일 때, 오빠가 방법을 제시하면 자기가 큰 방을 가지면서도 최대한 돈을 적게 내기 위해 6만 원을 주겠다고 할 거야. 동생은 자기가 생각하는 큰 방의 가치인 5만 원보다 6만 원이 크니까 작은 방을 고르겠지. 반면 동생이 방법을 제시한다면 자기가 작은 방을 갖는 대신 9만 원을 달라고 할 거야.

따라서 역할도 공평하게 정해야 해. 게임이론가의 대안은 거부권이야. 분배 방법이 맘에 안 들면 거부하고 다시 협상하도록 말야. 오른쪽을 참고해서 가장 맘에 드는 방식으로 협상을 해봐!