d라이브러리

라이트 아웃이 가장 유명하지만 불 끄는 게임의 원조는 ‘매직 스퀘어’예요. 1978년 미국 항공우주국 출신 게임 디자이너 밥 도일은 ‘메를린’이라는 게임기를 만들어 선보였어요. 메를린으로는 틱택토를 포함해 6가지 게임을 즐길 수 있는데, 그중 수학적으로 가장 흥미로운 건 매직 스퀘어예요.

매직 스퀘어는 가로, 세로 각각 3칸으로 이뤄진 버튼의 불을 끄고 켜서 결과적으로 가운데 불만 꺼지도록 만드는 게임이에요. 그런데 버튼을 누르면 이웃한 버튼의 불도 꺼지고 켜져서 생각보다 쉽지 않아요. 예를 들어 모퉁이의 버튼을 누르면 해당 버튼과 그 버튼에 이웃한 버튼 2개와 대각선 버튼까지 총 4개의 불의 상태가 바뀌어요(그림❶). 모서리 가운데 버튼을 누르면 양옆에 이웃한 버튼 2개를 포함해 버튼 3개의 상태가 바뀌고(그림❷), 가운데 버튼을 누르면 상하좌우 버튼까지 총 5개의 상태가 바뀌지요(그림❸).

1987년 캐나다 수학자 도널드 펠티에는 매직 스퀘어를 잘 할 수 있는 전략을 미국 수학회에서 발행하는 학술지 ‘미국 월간 수학’에 소개 했어요. 펠티에는 벡터를 이용해 불이 꺼지고 켜진 상태를 나타냈어요.
먼저 불이 켜진 상태를 1로, 꺼진 상태를 0으로 나타내요. 가장 위쪽 버튼부터 왼쪽에서 오른쪽 방향으로 읽어가며 불의 상태를 나타내면 길이가 9인 ‘초기 이진 벡터’를 만들 수 있어요. 초기 상태에서 누른 버튼의 상태를 모두 벡터로 나타내면 총 9개의 이진 벡터가 만들어져요. 만약 초기 이진 벡터가 모두 0이라면, 버튼 3을 눌렀을 때 이진 벡터는 (0, 1, 1, 0, 1, 1, 0, 0, 0)이 되지요. 이렇게 만든 이진 벡터를 벡터를 모두 더해서 결과적으로 (1, 1, 1, 1, 0, 1, 1, 1, 1)이 되게 만들면 게임을 끝낼 수 있답니다. 이때 ‘더한다’는 건 이진법 덧셈과 의미가 조금 달라요. 0+0=0, 1+0=0+1=1이지만, 1+1=0이기 때문이에요. 이진법처럼 자릿수가 늘어나지 않아요.

미니 라이트 아웃은 토러스 구조

라이트 아웃은 1995년 미국의 비디오 게임회사 ‘타이거 토이즈’가 만들었어요. 가로, 세로 각각 5칸에 불을 끄고 켤 수 있는 버튼이 있어요. 버튼을 누르면 그 버튼과 가로와 세로로 이웃한 불의 상태가 반대로 바뀌어요. 매직 스퀘어와 달리 대각선은 바뀌지 않아요. 라이트 아웃에서는 모든 불을 끄는 게 목표랍니다.

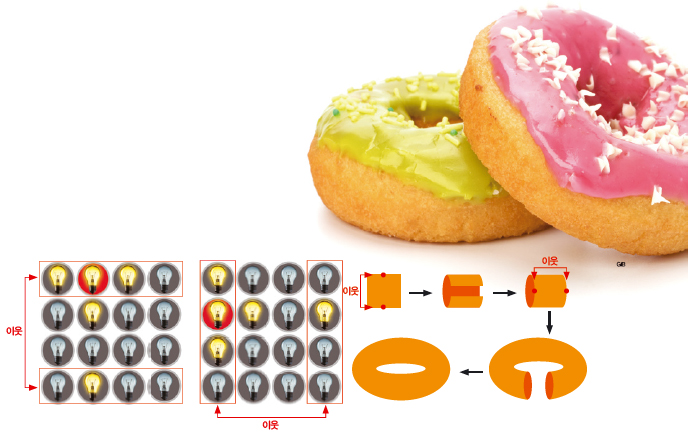
칸이 4개인 미니 라이트 아웃도 있는데, 라이트 아웃과 달리 버튼을 누르면 무조건 5개의 상태가 바뀌어요. 라이트 아웃에선 모서리 가운데 있는 버튼을 누르면 이웃한 3개의 버튼을 포함해 4개의 상태가 바뀌지요. 그런데 미니 라이트 아웃에선 맨 위와 맨 아래, 가장 왼쪽과 가장 오른쪽이 이웃한 것으로 설정돼 있어 무조건 5개의 상태가 바뀐답니다.

수학에서는 이런 구조를 ‘원환면’ 또는 ‘토러스’라고 부르지요. 토러스는 위상수학에서 자주 등장하는 도형으로, 사각형과 위상동형이에요. 사각형에서 마주보는 두 변을 이어 붙이면 토러스가 만들어지기 때문이에요.

연립방정식으로 라이트 아웃 깨기

매직 스퀘어와 라이트 아웃 모두 일차 연립방정식을 세워 해결할 수 있어요. 여기서는 가장 쉽게 가로, 세로 2칸인 초미니 라이트 아웃을 생각해 봐요. 게임의 규칙은 라이트 아웃과 같아요. 버튼 하나를 누르면 상하좌우에 이웃한 버튼까지 총 3개의 상태가 바뀌어요. 불이 켜진 상태를 1, 커진 상태를 0이라고 하면 어떤 버튼( )을 누르느냐에 따라 다음과 같이 불의 상태가 4가지로 바뀌지요.

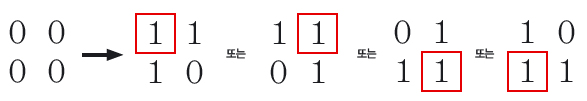
그럼 이제 초미니 라이트 아웃 게임을 즐겨볼까요? 다음과 같이 불이 들어와 있을 때 버튼을 최소로 눌러 불이 모두 꺼지게 만들어 보세요. 먼저 직관에 맡겨 답을 찾고, 이후 수학적으로 풀어 봅시다.

제 생각에는 버튼을 2번만 누르면 불을 모두 끌 수 있겠네요. 먼저 첫 번째 버튼을 누르고 마지막 버튼을 누르면 되니까요. 이게 최소인지 수학적으로 따져볼게요.

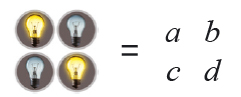
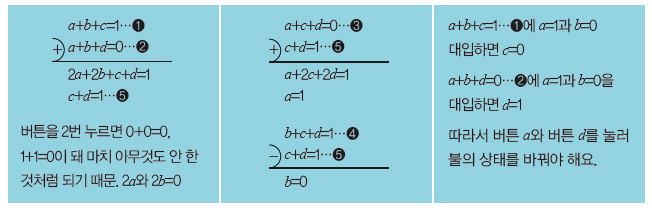
각 버튼을 위와 같이 문자를 써서 나타낸 다음 규칙을 식으로 표현해요. 여기서도 0+0=0,1+0=0+1=1, 1+1=0이에요. a에 불이 켜져 있으므로 규칙에 의해 a+b+c=1…❶이 됩니다. a와 d에 모두 불이 켜져 있어 a+b+d=0…❷이 되지요. 같은 방식으로 a+c+d=0…❸, b+c+d=1…❹이 됩니다. 이제 식을 풀어 볼게요.

라이트 아웃 게임의 모양이 꼭 정사각형일 필
요는 없답니다. 다양한 도형 위에 불이 들어오

는 버튼을 그려 게임을 즐길 수 있어요. 이참에 나만의 라이트 아웃 게임을 만들어 보는건 어떨까요? 이왕이면 C언어나 자바와 같은 언어를 이용해 직접 라이트 아웃 게임을 만들어 보세요. 라이트 아웃 게임을 짜는 소스 코드는 인터넷에서 쉽게 찾을 수 있어요. 소스 코드를 보고 응용해 나만의 게임을 만들면 더 재밌지 않을까요?


김종락
강대학교 수학과 교수는 포스텍 수학과를 졸업하고, 서울대학교에서 석사 학위를 받았습니다. 미국 일리노이주립대학교 시카고캠퍼스에서 박사 학위를 받았습니다. 주요 연구 분야는 부호론과 암호론, 산업수학, 인공지능입니다. 2004년 캐나다 조합론연구소에서 주는 커크만 메달을 한국인 최초로 받았습니다. 2016년부터 대한수학회 수학문화 앰배서더로 활동 중이며, ‘감성 수학레드’라는 스타트업을 운영하고 있습니다.