d라이브러리

방금 우리가 탄 차가 쌍곡 평면에 접어 들었어. 조사한 바에 따르면 이 동네는 우리가 사는 동네와 무척 달라. 친구 집 까지 가는 동안 들어 봐.

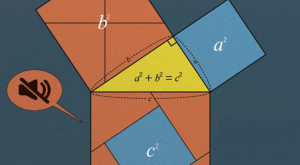
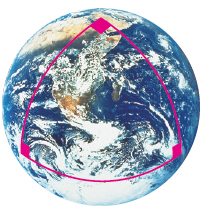
지구는 동그란 구에 가깝고 우리는 구의 표면에 살고 있잖아? 평평한 땅 위에서 직선을 따라 걸을 수 있고, 운동장에 납작한 정삼각형을 크게 그릴 수 있지. 사실은 구면에 있는 곡선을 따라 걷고, 운동장에 그린 삼각형도 수박위에 그린 그림처럼 휘어 있지만 우리는 그 사실을 알기만 할 뿐 느낄 수는 없어.

그럼 이 동네는 뭐가 다를까? 쌍곡 평면에 사는 주민도 평평한 땅 위에 정삼각형을 그릴 수 있어. 그 사람들은 모든 내각이 60°인 정삼각형을 그리고 있다고 생각하겠지. 그런데 실제로는 그렇지 않단다.

쌍곡 평면 밖에 있는 사람은 이 삼각형이 실제로 어떻게 생겼는지 볼 수 있지만, 쌍곡 평면에 사는 주민은 쌍곡 평면을 벗어나야만 그 모습을 볼 수 있어. 우주선을 쏘아 올린 덕분에 우주에서 보는 지구의 모습을 알게 된 우리처럼 말이야.


밖에서 봐야 알 수 있는 세계

18세기에 살았던 수학자 프리드리히 가우스 덕분에 인류는 쌍곡 평면에 그린 그림이 쌍곡 평면 밖에서 어떻게 보이는지 알 수 있었지. 쌍곡 평면에 사는 주민이 그린 정삼각형은 쌍곡 평면 밖에서는 각 변을 삼각형 안으로 눌러놓은 것처럼 보인대. 이 삼각형은 내각의 합이 180° 이하야.

가우스가 연구하고 헝가리 수학자 보여이야노시가 발표한 쌍곡기하학은 분명 획기적이었어. 그렇다고 해서 쌍곡 평면에 대해 모두 알 수 있었던 건 아니야. 지금도 ‘쌍곡 평면이 어떻게 생겼는지’ 아는 사람은 드물어. 평면기하학과 다른 새로운 학문 중 하나인 구면기하학은 구면 위의 기하를 다루는데, 구가 어떻게 생겼는지 모르는 사람은 드문 것을 생각하면 무척 놀라운 일이야.

“목욕탕 안에 치약과 비누를 모아둔 사물함이 일렬로 있어요. 맞은편에 거울이 하나 있고, 거울 앞에 사람들이 사물함 줄과 나란히 앉아 목욕하고 있어요. 거기에 가보세요.”

목욕탕 주인이 날 알아보고 친구가 어디에 있는지 알려주면서 쌍곡 목욕탕 전용 지도를 쥐어줬어. 사물함과 나란히 앉아서 목욕을 한다는건 사물함 줄과 사람들의 줄이 평행하다는 뜻이야. 즉, 사물함 줄과 평행하면서 거울 앞을 지나가는 선을 지도에서 찾으면 돼.

하지만 몇 시간째 친구도, 목욕하는 사람들의 줄도 찾지 못했어. 지도를 준 목욕탕 주인을 찾아가 지도가 잘못된 것이 아닌지 물었는데, 그제야 친구를 찾을 수 없었던 이유를 알 수 있었어.

쌍곡 평면의 지도에서는 ➊원점을 지나는 지름의 일부 또는 ➋양 끝이 원주와 90°로 만나는 곡선이 직선이야. 직선 바깥의 한 점을 지나는 평행선도 ➊ 또는 ➋에 해당하면서 동시에 원래 직선과 만나지 말아야 해.

이런 조건을 미리 알고 있었다고 해도 친구를 찾을 확률은 아주 낮아. 직선 바깥의 한 점을 지나는 평행선이 무한히 많이 있기 때문이야. 일반적인 평면 위에서는 이런 평행선이 단 하나뿐이어서 친구를 찾을 수 있었겠지만, 쌍곡 평면을 나타내는 지도는 쌍곡 평면에서 일어나는 일을 보여주기 때문에 그 속에 평행선이 무수히 많을 수밖에.


내각의 합이 0인 삼각형 타일링

쌍곡 평면 세계의 목욕탕에는 신기한 점이 또 있어. 바로 타일링! 어느 목욕탕이든 벽과 바닥이 한 가지 또는 두 가지 도형의 타일로 이뤄져있어. 정사각형 타일을 반복해서 붙이면 타일 4장이 한 점에서 만나. 정사각형의 한 내각의 크기가 90°이기 때문에 4장이 모여야 360°를 채울 수 있거든. 한 내각의 크기가 120°인 정육각형 타일은 한 점에 3장이 모이지. 그런데 목욕탕 바닥을 한번 봐. 정육각형 타일 4장이 한 점에서 만나고 있잖아?

주변의 육각형이 찌그러져 보이기는 하지만, 정육각형을 나타낸 건 확실해. 왜냐하면 지도의 원점에서 먼 곳일수록 실제로는 무한히 멀고 넓은 지역을 나타내거든. 지도 변두리에서 볼 수 있는 작은 도형도 실제로는 가운데에 있는 정육각형과 모양과 넓이가 똑같은 정육각형 지역을 나타내.

정육각형 4개가 한 점에서 만나는 이유는 쌍곡 평면에서는 정육각형의 내각이 120°가 아닌, 90°이기 때문이야. 구면에서 아무리 반듯한 정삼각형을 그리려고 해도 내각의 합이 180°를 넘는 것처럼, 쌍곡 평면이 휘고 뒤틀린 까닭에 그 위에 그린 정육각형의 한 내각이 작아질 수 있어.