d라이브러리

비례는 분수와 소수, 곱셈과 나눗셈, 닮음과 삼각법, 단위 환산, 기울기, 비율로서의 확률, 자료의 비교, 수와 연산, 도형, 측정, 함수와 미적분, 확률, 통계 등 다양한 영역과 관련이 있습니다. 수학 외적으로는 인구밀도나 축척, 속도, 힘, 농도, 이익률과 손실률, 지리학, 과학, 경제학, 역학 등 다양한 학문과 관련 있을 뿐만 아니라 음료의 농도나 약의 성분비, 건축물이나 조형물의 비와 같은 일상생활과도 관련이 있습니다.

따라서 비와 비례를 배우기 시작할 때 일상생활에서 사용하는 비와 비례의 사례를 찾아오는 과제를 내주면 좋습니다. 비는 ‘두 대상 사이의 곱셈적 관계’이고, 비례는 ‘두 비의 상등’을 의미합니다.
 

 

예를 들어, 바나나 2개와 우유 5컵을 섞어 바나나우유를 만든다고 해봅시다. 그러면 바나나가 4개, 6개, 8개, …로 늘어날 때 우유도 10컵, 15컵, 20컵, …과 같이 늘어납니다. 즉, 바나나가 2배, 3배, 4배, …가 될 때, 우유도 2배, 3배, 4배, …가 됩니다. 이를 공변성이라 합니다. 바나나와 우유의 비는 2개와 5컵, 4개와 10컵, 6개와 15컵, …과 같이 변하지만 2:5라는 관계는 변하지 않습니다. 이는 일정성이라 합니다. 이 두 성질을 파악하는 것이 비와 비례의 본질입니다.

비의 성질은 공변성과 일정성을 바탕으로 추론할 수 있습니다. 5학년 때 배우는 ‘통분과 약분’과 연계하면 학생들이 더 쉽게 이해할 수 있습니다.
 

비례 학습 지도에서 중요한 건 공변성과 일정성에 대한 이해에 바탕을 둔 추론 능력의 향상입니다.



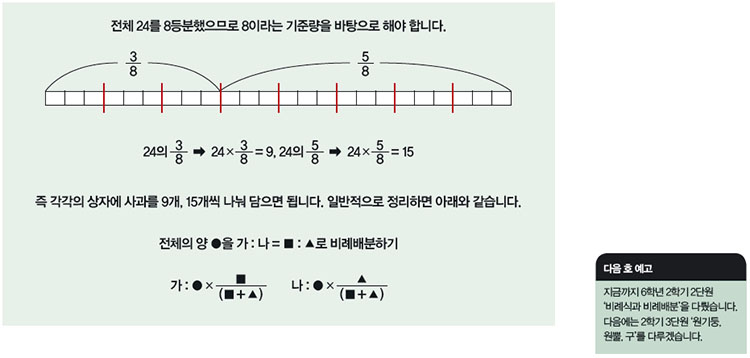
전체를 정해진 비로 배분하는 것을 비례배분이라고 합니다. 비례배분의 핵심은 정해진 비의 전항과 후항의 합을 분모로 하는 분수의 비로 고치는 것입니다.

예를 들어 24개의 사과를 3:5의 비로 2개의 상자에 나누어 담으려고 할 때 간혹 학생들은 3:5만 보고 24에 3/5을 곱하기도 합니다. 이런 실수를 막기 위해서는 비례배분에서 기준에 대한 개념을 명확히 하는 것이 필요합니다.