

지난 1월 새로운 거대 소수가 발견됐다. 지금까지 발견됐던 소수도 굉장히 큰 수였는데, 이번에 발견된 소수는 그보다 더 크다고 한다. 글자 크기를 4포인트로 작게 인쇄해도 무려 500쪽짜리 책이
되며, 4초에 숫자 10개씩 쓴다고 하면 전체를 쓰는 데 3개월이 넘게 걸린다. 이 어마어마한 수를 어떻게 찾아낸 걸까?

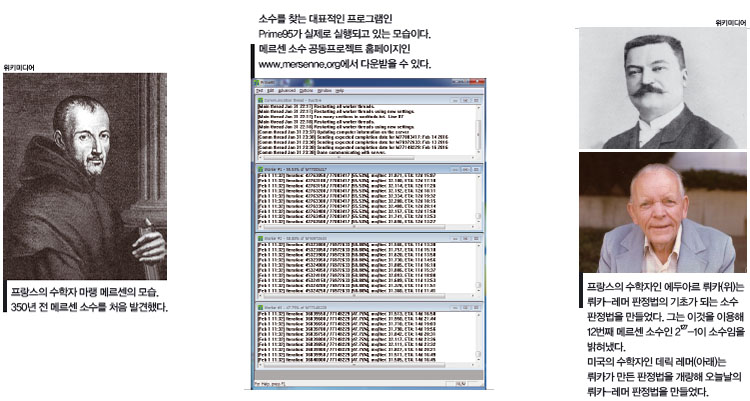
이번에 찾은 소수는 49번째 ‘메르센 소수’이기도 하다. 메르센 소수란 17세기 프랑스의 수학자였던 마랭 메르센의 이름을 딴 소수로, 2의 거듭제곱에서 1을 뺀 모양의 소수를 의미한다. 가장 큰 소수를 발견했다고 하면 보통 메르센 소수다.
쿠퍼 교수는 ‘메르센 소수 공동프로젝트’(GIMPS) 소속으로, 이 단체는 ‘Prime95’나 ‘MPrime’같은 소프트웨어를 이용해 메르센 소수를 찾는다. 메르센 소수 공동프로젝트에서 쓰는 프로그램으로 소수를 검증해보는 것은 컴퓨터 하드웨어의 성능을 시험해보는 데 쓰이기도 한다. 실제로 Prime95를 이용해 인텔 CPU의 결함을 찾아내기도 했다.
메르센 소수를 찾아서!
메르센은 소수의 규칙을 찾는 데 빠져 있었다. 그러던 중 p가 1보다 큰 자연수일 때
 이 소수일지도 모른다는 생각을 하게 된다. 하지만 p가 어떤 수든 무조건
이 소수일지도 모른다는 생각을 하게 된다. 하지만 p가 어떤 수든 무조건  이 소수인 건 아니었다.
이 소수인 건 아니었다.
메르센은 지수 p가 소수일 때  이 소수가 된다고도 생각했다. 그러나 p가 소수인 11일 때는 11-1=2047이고, 2047은 23×89로 소인수분해가 되는 것을 알게 됐다. 즉 이때는 소수가 아닌 것이다. 소수의 규칙은 쉽게 찾아지지 않았다. p의 크기를 키워가며
이 소수가 된다고도 생각했다. 그러나 p가 소수인 11일 때는 11-1=2047이고, 2047은 23×89로 소인수분해가 되는 것을 알게 됐다. 즉 이때는 소수가 아닌 것이다. 소수의 규칙은 쉽게 찾아지지 않았다. p의 크기를 키워가며  이 소수가 되는 숫자들을 찾던 메르센은 p가 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257일 때만 소수라고 발표한다.
이 소수가 되는 숫자들을 찾던 메르센은 p가 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257일 때만 소수라고 발표한다.
나중에는 이것 또한 틀린 것으로 결론이 났다. 1903년에는 p가 67, 1931년에는 p가 257일 때 이 소수가 아닌 것이 밝혀진 것이다. 그래도 메르센의 노력은 결코 헛되지 않았다. 오늘날 메르센 소수는 컴퓨터를 이용해 소수를 찾을 때 쓰이기 때문이다.
이 소수가 아닌 것이 밝혀진 것이다. 그래도 메르센의 노력은 결코 헛되지 않았다. 오늘날 메르센 소수는 컴퓨터를 이용해 소수를 찾을 때 쓰이기 때문이다.
새로 발견되는 소수는 왜 대부분 메르센 소수?
새로운 소수가 발견됐다는 소식을 접하고 보면, 그 소수는 보통 메르센 소수다. 그것은 메르센 소수를 찾는 획기적인 알고리즘 때문이다. 일반적으로 자연수 n이 소수인지 판별하기 위해서는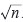 보다 작은 모든 소수로 나눠떨어지지 않는 것을 확인하면 된다. 그러나 이 방법은 수가 커질수록 소수인지 아닌지 판별하기 매우 어렵다. 계산해야 하는 양이 너무 많아지기 때문이다.
보다 작은 모든 소수로 나눠떨어지지 않는 것을 확인하면 된다. 그러나 이 방법은 수가 커질수록 소수인지 아닌지 판별하기 매우 어렵다. 계산해야 하는 양이 너무 많아지기 때문이다.
이것과 비교해 메르센 소수는 상대적으로 쉽게 찾을 수 있다. 메르센 소수를 찾는 ‘뤼카-레머 판정법’을 쓰면 비교적 짧은 과정을 통해 소수인지 아닌지 알 수 있기 때문이다. 메르센 소수를 찾는 대표적인 프로그램인 Prime95에도 이 판정법이 쓰이고 있다.
이 말은 메르센 소수 외의 소수를 찾는 획기적인 방법이 없다는 말이기도 하다. 예를 들어 메르센 소수가 발견됐더라도, 그 소수의 쌍둥이 소수를 확인하는 일은 거의 불가능에 가깝다. 쌍둥이 소수란 그 차가 2인 소수를 말하는데 11, 13이나 17, 19 같은 소수 쌍을 의미한다. 즉 뤼카-레머 판정법을 통해 메르센 소수를 찾았더라도, 그 수의 앞뒤로 2만큼 차이가 나는 수가 소수인지 아닌지 판단하는 것은 매우 어렵다는 이야기다.
뤼카-레머 판정법을 이용해 컴퓨터로 메르센 소수를 찾는 데 처음으로 성공한 사람은 미국의 수학자 라파엘 로빈슨이다. 그는 1950년에 미국 국립표준기술연구소에서 만든 ‘스왁’이라는 초창기 디지털 컴퓨터를 이용해 1952년에만 무려 5개의 메르센 소수를 찾아냈다. 컴퓨터로 메르센 소수를 찾기 전까지 가장 큰 소수는 에두아르 뤼카가 발견한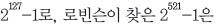 이보다 4배 이상 자릿수가 크다.
이보다 4배 이상 자릿수가 크다.


 이 소수가 된다고도 생각했다. 그러나 p가 소수인 11일 때는 11-1=2047이고, 2047은 23×89로 소인수분해가 되는 것을 알게 됐다. 즉 이때는 소수가 아닌 것이다. 소수의 규칙은 쉽게 찾아지지 않았다. p의 크기를 키워가며
이 소수가 된다고도 생각했다. 그러나 p가 소수인 11일 때는 11-1=2047이고, 2047은 23×89로 소인수분해가 되는 것을 알게 됐다. 즉 이때는 소수가 아닌 것이다. 소수의 규칙은 쉽게 찾아지지 않았다. p의 크기를 키워가며  이 소수가 되는 숫자들을 찾던 메르센은 p가 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257일 때만 소수라고 발표한다.
이 소수가 되는 숫자들을 찾던 메르센은 p가 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257일 때만 소수라고 발표한다.나중에는 이것 또한 틀린 것으로 결론이 났다. 1903년에는 p가 67, 1931년에는 p가 257일 때
 이 소수가 아닌 것이 밝혀진 것이다. 그래도 메르센의 노력은 결코 헛되지 않았다. 오늘날 메르센 소수는 컴퓨터를 이용해 소수를 찾을 때 쓰이기 때문이다.
이 소수가 아닌 것이 밝혀진 것이다. 그래도 메르센의 노력은 결코 헛되지 않았다. 오늘날 메르센 소수는 컴퓨터를 이용해 소수를 찾을 때 쓰이기 때문이다.
새로 발견되는 소수는 왜 대부분 메르센 소수?
새로운 소수가 발견됐다는 소식을 접하고 보면, 그 소수는 보통 메르센 소수다. 그것은 메르센 소수를 찾는 획기적인 알고리즘 때문이다. 일반적으로 자연수 n이 소수인지 판별하기 위해서는
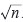 보다 작은 모든 소수로 나눠떨어지지 않는 것을 확인하면 된다. 그러나 이 방법은 수가 커질수록 소수인지 아닌지 판별하기 매우 어렵다. 계산해야 하는 양이 너무 많아지기 때문이다.
보다 작은 모든 소수로 나눠떨어지지 않는 것을 확인하면 된다. 그러나 이 방법은 수가 커질수록 소수인지 아닌지 판별하기 매우 어렵다. 계산해야 하는 양이 너무 많아지기 때문이다.이것과 비교해 메르센 소수는 상대적으로 쉽게 찾을 수 있다. 메르센 소수를 찾는 ‘뤼카-레머 판정법’을 쓰면 비교적 짧은 과정을 통해 소수인지 아닌지 알 수 있기 때문이다. 메르센 소수를 찾는 대표적인 프로그램인 Prime95에도 이 판정법이 쓰이고 있다.
이 말은 메르센 소수 외의 소수를 찾는 획기적인 방법이 없다는 말이기도 하다. 예를 들어 메르센 소수가 발견됐더라도, 그 소수의 쌍둥이 소수를 확인하는 일은 거의 불가능에 가깝다. 쌍둥이 소수란 그 차가 2인 소수를 말하는데 11, 13이나 17, 19 같은 소수 쌍을 의미한다. 즉 뤼카-레머 판정법을 통해 메르센 소수를 찾았더라도, 그 수의 앞뒤로 2만큼 차이가 나는 수가 소수인지 아닌지 판단하는 것은 매우 어렵다는 이야기다.
뤼카-레머 판정법을 이용해 컴퓨터로 메르센 소수를 찾는 데 처음으로 성공한 사람은 미국의 수학자 라파엘 로빈슨이다. 그는 1950년에 미국 국립표준기술연구소에서 만든 ‘스왁’이라는 초창기 디지털 컴퓨터를 이용해 1952년에만 무려 5개의 메르센 소수를 찾아냈다. 컴퓨터로 메르센 소수를 찾기 전까지 가장 큰 소수는 에두아르 뤼카가 발견한
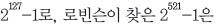 이보다 4배 이상 자릿수가 크다.
이보다 4배 이상 자릿수가 크다.















