d라이브러리

네덜란드 작가 디오니스 버거가 1965년에 쓴 소설<;스피어랜드>;를 바탕으로 한 같은 이름의 애니메이션에는 2차원 생명체인 헥스와 펑토가 3차원과 4차원으로 여행을 떠나는 내용이 나온다. 이 애니메이션의 마지막 장면에는 도넛 모양인 토러스가 나온다. 토러스는 차원과 어떤 관계일까?

지구가 둥글다는 주장은 오래전부터 있었지만 실제로 사람들이 지구가 구 모양이라고 믿기 시작한건 훨씬 나중의 일이었다. 극지방과 일부 대륙의 중 심부는 19세기까지 지도로 그려지지 않았다. 남극과 북극을 포함한 모든 지역을 지도로 그리기 전까지는 지구가 구 모양이라는 것을 확신할 수 없었다. 왜냐하면 지구가 토러스 모양일 수도 있어서다.

직사각형의 아랫변과 윗변을 붙이면 원기둥이 된다. 그리고 이 원기둥의 양 끝을 연결하면 도넛을 닮은 토러스가 된다. 토러스는 컴퓨터 게임 ‘팩맨’에서도 찾을 수 있다. 팩맨은 화면의 가장자리로 빠져나간 다음 곧바로 반대편 가장자리에서 나타난다. 이렇게 멀리 떨어진 것 같은 공간이 연결돼 있다는 게 토러스의 특징이다.

지구에서는 동쪽으로 계속 걸으면 결국 서쪽에서 처음 자리로 돌아온다. 마찬가지로 남쪽으로 계속 걸으면 결국 북쪽에서 처음 자리로 돌아온다. 만약 지구가 토러스라면 이 동서 방향 길과 남북 방향 길은 처음 자리를 빼고는 어느 곳에서도 교차하지 않는다. 이런 성질 때문에 토러스와 구면이 다르다.

사람들은 우주에서 지구를 촬영한 사진 덕분에 비로소 지구가 둥글다고 확신하기 시작했다. 그렇다면 우주의 모양을 알기 위해서는 우주 밖으로 나가야 한다. 그래서 수학자들은 3차원 공간의 모양을 상상하기 시작했다. 프랑스의 수학자 푸앵카레는 ‘3차원에서 두 물체가 특정 성질을 똑같이 가지고 있으면 두 물체는 같다’라고 추측했다. 쉽게 말하면, 밧줄을 달고 우주 끝까지 갔다가 되돌아 온 로켓에서 우주의 모양을 알 수 있다는 뜻이다. 밧줄 양끝을 끌어 당겨서 밧줄을 한군데로 모을 수 있으면 우주는 구 모양이다. 밧줄이 어딘가에 걸려서 한군데로 모아지지않으면 우주는 토러스 모양이라고 추측할 수 있다.

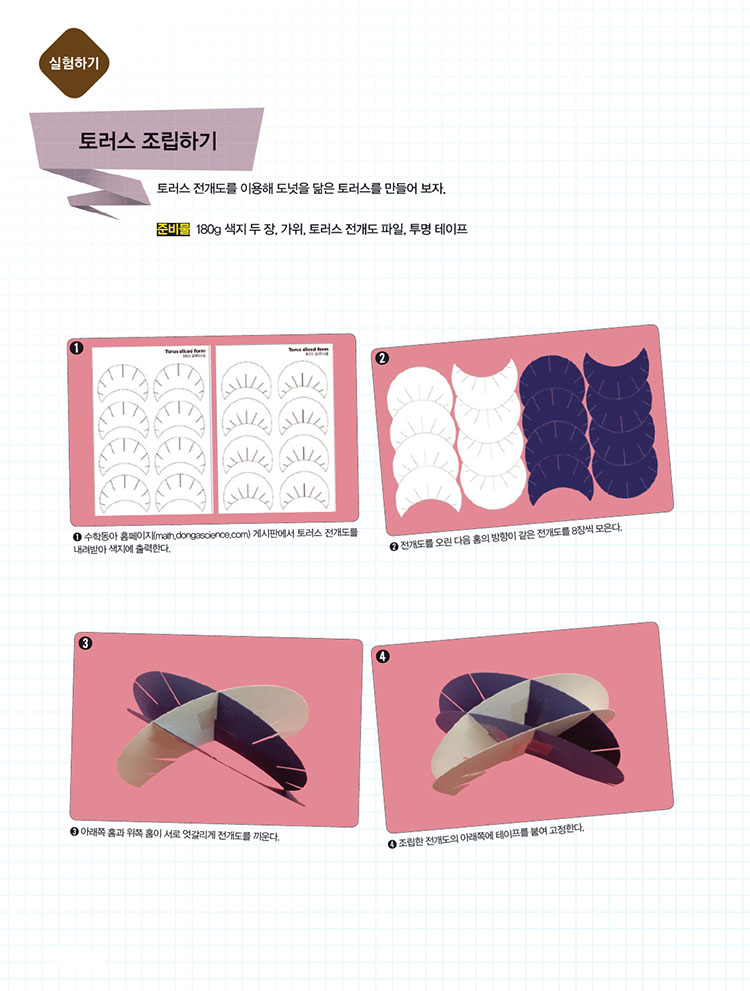
사물뿐만 아니라 우주의 모양을 추측하는 데 중요한 역할을 하는 토러스를 조립해 보자. 그리고 모양을 바꿔 새로운 토러스에도 도전해 보자.