d라이브러리

Prologue_ 대포클럽 회원들은 드디어 거대한 대포를 만들어 발사하는 데 성공합니다. 그리고 달을 향해 날아가는 대포알 속에는 바비케인과 미셸 아르당, 니콜이라는 3명의 모험가가 타고 있지요. 이들은 과연 무사히 달을 탐험하고 돌아올 수 있을까요?

숫자 대신 문자

“잘 들어보게.” 바비케인이 대수학을 모르는 친구에게 말했다. “이 기호들이 의미를 갖고 있다는 건 자네도 알겠지?”

바비케인은 설명하기 시작했다.

“d는 지구의 중심에서 달의 중심까지의 거리일세. 인력을 계산할 때 문제되는 건 중심이니까.”

“그건 알아.”

“r은 지구의 반지름.”

“r은 반지름이다. 좋아.”

“m은 지구의 질량, m은 달의 질량일세. 서로 끌어당기는 두 천체의 질량을 고려해야 돼. 인력은 질량에 비례하니까.”

바비케인이 다른 두 사람에게 대포알의 발사 속도를 계산하는 공식에 대해 설명하고 있습니다. 그런데 미셸과 니콜은대수학이 뭔지 잘 모르는 눈치입니다. 그래서 바비케인은 어쩔 수 없이 대수학에 대해 먼저 설명하고 있습니다.

대수학은 숫자 대신에 문자를 사용하여 수의 관계나 계산 법칙 등을 연구하는 수학의 한 분야입니다. 바비케인은 지구의 반지름을 ‘r’, 지구의 질량을 ‘m’으로 나타낸다고 설명하고 있습니다. 수를 문자로 나타내면 어떤 이득이 있을까요?

예를 들어, 우리는 2×3과 3×2가 똑같고, 5×6과 6×5가 똑같다는 사실을 잘 알고 있지만 숫자를 쓴다면 한눈에 들어오게 쓰기 쉽지 않습니다. 이 때, a×b=b×a라고 쓰면 매우 간편합니다. 이렇게 패턴을 찾아 내고 문자로 대체하면 공식을 만들 수 있습니다. 좀 더 복잡한, 중력의 크기를 나타내는 공식을 보고 생각해 봅시다.
 

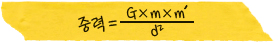
질량이 각각 m, m이고 거리가 d인 두 물체 사이에 작용하는 중력의 크기를 나타냅니다. 이 때 문자에 알맞은 수를 대입하면 중력의 크기를 구할 수 있습니다. 중력의 공식이 없어서 필요할 때마다 숫자로 일일이 계산해야 한다면 어떨까요? 그때 그때 계산 방법을 다시 확인해야 했을 것입니다. 공식을 만들어 일반화시킬 수 있다는 것은 대수학의 훌륭한 장점입니다.

포물선이냐, 쌍곡선이냐?
 

“그래.” 니콜이 말했다. “포탄은 쌍곡선이나 포물선을 그릴 거야.”

(중략)

그러자 니콜이 대답했다.

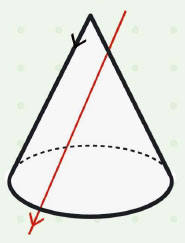
“포물선은 원뿔을 하나의 옆면에 평행한 평면으로 자를 때 나타나는 곡선이야.”

“아아, 그렇군!” 미셸은 만족스러운 투로 말했다.

“그건 박격포에서 발사된 포탄이 그리는 탄도와 아주 비슷하지.” 니콜이 덧붙여 말했다.
“잘 알았네. 그럼 쌍곡선은?”

“쌍곡선은 원뿔면과 그 축에 평행한 평면의 교점으로 생기는 제2급 곡선이라네. 서로 떨어져 있는 두 개의 지선으로 이루어져 있고, 이 두 지선은 두 방향으로 무한히 뻗어나갈 수 있지.”
 

대포알이 어떻게 날아갈지에 대해 이야기하고 있네요. 아마도 쌍곡선이나 포물선 둘 중 하나의 궤적을 그리며 날아갈것 같습니다. 먼저 포물선에 대한 설명이 이어집니다.

포물선은 원뿔을 옆면과 평행하게 잘랐을 때 그 단면에 나타난 곡선입니다. 포물선을 평면 위에 놓고 보면 어떨까요?평면 위에 한 점과 직선이 있을 때 점까지의 거리와 직선까지의 거리가 똑같은 점들의 집합을 이으면 바로 포물선이 됩니다. 실생활에서는 공을 던지거나 대포를 발사했을 때 공과 대포알이 움직이는 궤도가 바로 포물선이죠.

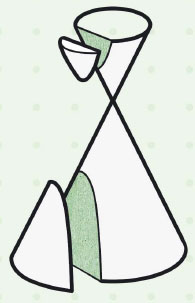
쌍곡선은 두 원뿔을 수직으로 잘랐을 때 그 단면에 나타난 곡선입니다. 원뿔 두 개를 모래시계처럼 붙여 놓은 모습을 상상해 보세요. 두 개의 원뿔을 수직으로 자르면 위와 아래에 두 개의 곡선이 생기는데, 이것이 바로 쌍곡선입니다. 평면 위에 두 점이 있을 때 두 점까지의 거리의 차가 일정한 점들을 쭉 이어도 쌍곡선을 그릴 수 있습니다. 쌍곡선의 두 곡선은 스스로 대칭일 뿐만 아니라 서로 대칭이기도 합니다.

모험가들이 대포알의 궤적으로 놓고 고민하는 이유는 포물선이나 쌍곡선이 모두 무한히 뻗어나가기 때문입니다. 대포알이 끝도 없이 뻗어 나갈 수 있기 때문에 걱정하는 것이죠.

달 주위에 타원을 그리다

“그럼 포탄의 진로는 쌍곡선도 포물선도 아니고, 끝없이 이어지는 무서운 곡선도 아니겠군?”

“그래. 열린 곡선이 아니라 닫힌 곡선이지.”

“그건 어떤 곡선인가?”

“타원이야. 포탄은 우주 공간으로 사라지지 않고 달 주위에서 타원형 궤도를 그리게 될 것 같아.”

“정말이야?”

“달의 위성이 되는 거지.”

“달의 달이 된다고?” 미셸 아르당이 외쳤다.
 

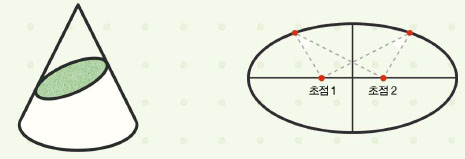
드디어 대포알의 궤도를 알아 내는 데 성공했습니다. 다행히 무한히 멀리 뻗어 나가지 않고 타원 궤도를 그리며 달 주위를 돈다고 하네요. 보통 타원이라고 하면 원을 대충 눌러 놓은 모양을 생각하죠? 수학적으로 타원을 정확히 어떻게 정의하는지 알아봅시다.

타원은 두 개의 점이 있을 때 각 점으로부터 거리의 합이 일정한 점들의 궤적입니다. 이 두 개의 점을 초점이라고 하지요. 두 초점이 가까울수록 눌린 정도가 작아 원에 가깝고, 멀수록 납작한 모양이 됩니다. 타원도 원뿔을 자른 단면으로 나타낼 수 있습니다. 원뿔을 수평으로 자르면 그 단면은 원이 되지만, 비스듬하게 잘랐을 때의 단면은 타원이 되거든요.

타원의 중심은 두 초점의 중간에 있는 점인데, 원과 달리 반지름이 일정하지 않습니다. 두 초점을 지나는 긴 지름을 장축이라 하며, 장축에 수직이면서 중심을 지나는 짧은 지름을 단축이라고 합니다.

달 주위를 도는 대포알이 원이 아니라 타원을 그린다고 쓴 이유는 실제로 태양계의 행성이 모두 타원 궤도로 태양 주위를 돌기 때문입니다. 이것이 바로 그 유명한 케플러의 제1법칙이지요. 작가인 쥘 베른은 달의 중력에 사로잡힌 대포알도 케플러의 법칙을 따를 것이라 생각했던 것입니다.

비율로 따지면 누가 높을까?

달의 최고봉은 7603미터이고, 이것은 지구의 일부 산보다는 낮다. 지구의 산들 가운데 일부는 달의 산보다 1000미터 내지 1200미터는 더 높다. 하지만 주의해야 할 점이 하나 있다. 달과 지구의 산을 달과 지구의 부피와 비교하면, 상대적으로는 달의 산이 지구의 산보다 훨씬 높다. 달의 높은 산들은 달지름의 470분의 1인 반면, 지구의 높은 산들은 지구 지름의 1440분의 1에 불과하다. 지구의 산이 달의 산과 같은 비율에 도달하려면 수직 고도가 무려 25킬로미터가 되어야 한다.

대포알을 탄 세 명의 모험가는 마침내 달을 가까이 지나가면서 달의 지형을 관찰합니다. 달에도 지구처럼 높은 산이 여기저기 솟아 있는데, 가장 높은 산의 높이가 7603m라고 합니다. 지구에서 가장 높은 산은 에베레스트 산으로 높이가 8848m이므로, 단순히 비교하면 에베레스트 산이 더 높습니다. 하지만 쥘 베른은 지구와 달의 크기에 대한 산의 높이 비율로 어느 산이 높은지 따져야 한다고 말합니다.

지구의 반지름은 약 6400km고, 달의 반지름은 약 1740km입니다. 대략 3.7배 차이가 납니다. 달을 지구 크기와 똑같이확대하면 어느 쪽 산이 높은지 알 수 있습니다. 달의 반지름에 3.7을 곱하면 지구의 반지름과 비슷하므로, 달에 있는 산의 높이에도 3.7을 곱해 줘야 합니다. 그러면 달에서 가장 높은 산의 높이는 28,131m가 됩니다. 쥘 베른의 계산과는 조금 다르지만 에베레스트 산보다 훨씬 높은 것은 분명합니다.

이렇게 쥘 베른의 주장처럼 비율로 따져 보는 것을 가리켜 우리는 ‘상대적’이라고 합니다. 단순히 산의 높이만을 비교하는 게 아니라 ‘지구의 크기에 대한 산의 비율’과 ‘달의 크기에 대한 산의 비율’을 비교하는 것이죠. 반대로 단순히 산의 높이만을 비교하는 것을 ‘절대적’이라고 합니다.

다른 예를 들어 볼까요? 어떤 학생은 정원이 30명인 반에서 2등을 했고, 어떤 학생은 정원이 300명인 학교에서 5등을 했습니다. 이 때 절대적인 등 수만을 보면 2등을 한 학생이 더 잘한 것 같지만, 상대적으로 보면 300명 중의 5등이 더 잘한 것이지요.

이처럼 지구와 달에 있는 산의 높이를 비교할 때, 절대적으로 보면 지구의 산이 높지만 상대적으로 보면 달의 산이 높습니다. 어떻게 보느냐에 따라 기준이 달라지는 거지요.

거리에 따라 속도가 달라진다
 

포탄이 달의 위성이 된다면, 달에 가장 가까이 다가갔을 때는‘근월점’에 있고 달에서 가장 멀리 떨어졌을 때는‘원월점’에 있다고 말할 수 있다. 포탄은 근월점에 있을 때 속력이 가장 빨라지고, 원월점에 있을 때 속력이 가장 느려질 것이다. 지금 포탄은 원월점을 향해 나아가고 있었다. 그 속력은 원월점에 도달할 때까지 계속 줄어들고, 달에 가까워질수록 조금씩 속력이 빨라질 거라고 바비케인이 판단한 것은 당연한 일이었다.

앞서 대포알이 달의 위성이 된다면 타원 궤도를 그린다고 했습니다. 이 때 달은 타원의 중심이 아닌 두 초점 중 하나가 됩니다. 바로 케플러의 제1법칙이지요. 따라서 대포알이 달 주위를 공전하는 동안 둘 사이의 거리가 변합니다. 거리가 가장 가까울 때를 ‘근월점’, 가장 멀 때를 ‘원월점’이라고 부르는 것까지는 쉽습니다. 그런데 근월점에서 속력이 가장 빠르고, 원월점에서 속력이 가장 느리다는 건 무슨 이야기일까요?

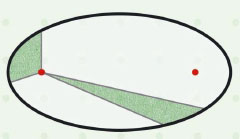
이것은 케플러의 제2법칙과 관련이 있습니다. 제2법칙은 면적-속도 일정의 법칙으로, 행성과 태양을 연결하는 가상의 선분이 같은 시간 동안 쓸고 지나가는 면적은 항상 같다는 내용입니다.

위 그림에서 볼 수 있듯이 일정 시간 동안 같은 면적을 만들기 위해서는 행성이 태양에 가까울 때 빨리 움직이고 멀 때 천천히 움직여야 합니다.

달 주위를 도는 대포알도 마찬가지로 케플러 제2법칙을 따릅니다. 따라서 달에 가까울수록 속도가 빠르고 멀수록 속도가 느려집니다. 대포알이 달에서 가장 먼 원월점으로 다가가고 있는 중이므로 대포알의 속도가 줄어들거라는 바비케인의 예측은 정확했습니다. 그리고 모험가들은 마지막 수단으로 속도가 줄어들 때 역추진 로켓을 점화해 달에 착륙하려고 합니다.