지난 9월 17일, 2006년 필즈상 수상자인 테렌스 타오교수가 화제가 됐다. 83년 묵은 수학 문제를 획기적인 방법으로 순식간에 풀어 인터넷에 발표했기 때문이다. 자신의 블로그에 이 문제가 정수론의 오래된 문제인 엘리엇 추측과 관련이 있다는 글을 남긴 지 6일 만의 일이다. 또한 이 문제가 그와 인연이 깊은 헝가리의 수학자 폴 에르되시가 낸 문제라 더욱 관심을 받았다.
과연 타오 교수는 어떤 문제를 풀었을까?
“이 문제를 푼 사람에게는 상금으로 500달러(현재 가치로 약 1천 750만 원)를 주겠습니다.”
83년 전 폴 에르되시는 ‘에르되시 불일치 문제’라는 정수론 문제를 내고 상금을 걸었다. 이후 많은 수학자들이 이 문제에 도전장을 내밀었지만, 번번이 실패하고 말았다. 문제 자체는 그리 어려워 보이지 않았지만, 막상 풀려고 하면 어떻게 문제에 접근해야 할지 막막했기 때문이다.
에르되시 불일치 문제는 1과 -1, 달랑 두 수하고만 관련이 있다. 1과 -1을 골고루 잘 섞은 뒤 길게 늘어놓은 수열이 있다고 하자. 임의의 수 n을 고른 다음 n의 배수번째에 있는 수만을 골라낸다. 이렇게 만든 부분 수열에 1과 -1이 골고루 섞여 있게 할 수 있는지 묻는 문제다. 즉 부분수열의 합(부분합)과 0 사이의 차이를 항상 작게 만들 수 있냐는 것이다. 예를 들어 100만을 기준으로 삼자. 100만보다 큰 부분 수열의 합이 있는지, 혹은 -100만보다 작은 부분 수열의 합이 있는지 묻는 것이다. 있다면 1과 -1이 골고루 섞여 있지 않은 것이다. 부분 수열을 결정하는 수n은 3이나 1000 등 어떤 수도 될 수 있다.
그런데 타오 교수에 의하면 1과 -1이 골고루 섞여 있는 건 불가능하다. 즉 1과 -1을 어떻게 늘어놓아도 적당히 n을 잘 골라서 n의 배수번째 수들을 더해가다 보면 그 부분합과 0 사이의 차이가 100만보다 커지는 순간이 생기는 n을 반드시 찾을 수 있다.
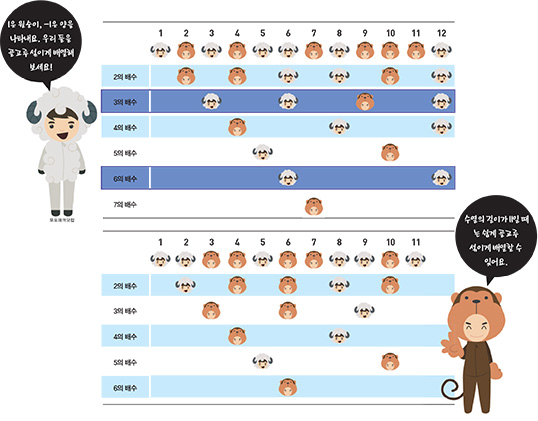
간단한 경우를 살펴보기 위해 기준을 100만 대신 1로 바꾸고, 1과 -1도 원숭이와 양으로 바꿔 생각해 보자. 우선 원숭이와 양 12마리를 잘 나열한다. 모든 n에 대해 n의 배수번째에 나타난 원숭이의 수와 양의 수를 세었을 때 그 차이가 항상 1을 넘지 않게 할 수 있을까? 만약 그림과 같이 나열돼 있다면 3의 배수와 6의 배수에서 양이 2마리 더 많아 골고루 섞여 있지 않다. 하지만 총 11마리가 있다면 모든 부분 수열에서 1을 넘지 않게 만들 수 있다. 즉 골고루 섞이게 배열할 수 있다.
증명만 1만 5000쪽!
여기까지가 불과 몇 년 전까지 알려져 있던 내용이다. 1과 -1을 길게 늘어놓았을 때 앞에서 부터 12개 수만 알면, 거기서 벌써 부분합과 0 사이의 차이가 항상 1보다 크게 할 수 있다. 물론 적당한 n을 잘 골라 n의 배수번째 수들을 더해나갔을 때 말이다. 사실 문제 자체는 중학생도 이해할 수 있을 정도로 그리 어렵지 않다. 하지만 이를 증명하는 것은 매우 어렵다. 이를 단편적으로 보여주는 것이 지난해 2월 발표된 논문이다.
영국 리버풀대 알렉세이 리시차와 보네스 코네브는 적당한 n에 대해 n의 배수번째 수들의 부분합과 0 사이의 차이가 2보다 큰 경우가 반드시 있다는 사실을 증명했다. 이때 전체 수열의 길이가 1161이라고 것도 밝혀냈다. 기준이 1일 때 1과 -1을 12개까지 알아야 했다면, 2일 때는 1161개까지 살펴봐야 한다는 것이다.
연구팀은 논리식을 만들어 컴퓨터로 풀었다. ‘첫 번째가 +1이면 두 번째도 +1, 세 번째는 -1이어야 한다’처럼 여러 가지 경우를 따져 프로그램을 짰다. 그 결과 증명 내용만 13GB에 달했다. 계산 결과만 1만 5000쪽이나 됐다. 위키피디아의 정보량이 10GB정도라고 하니 위키피디아의 정보량보다 증명 분량이 훨씬 많은 셈이다. 즉 획기적인 아이디어 없이 모든 경우를 일일이 따져 문제를 해결하는 건 불가능하다.
함께 풀어야 답이 보인다
그렇다면 이처럼 어려운 문제는 어떻게 해결할 수 있을까? 수학자들은 여럿이서 머리를 맞대야 한다고 생각했다. 그 선두에 1998년 필즈상 수상자인 티머시 가워스 교수가 있다. 2009년말, 그는 에르되시 불일치 문제를 포함한 여러 수학 문제를 온라인에서 함께 풀자고 제안했다. 일명 ‘폴리매스(POLYMATH)’ 프로젝트다. 가워스 교수는 인터넷 사이트를 만들고 수학문제를 소개했다. 그러면 수학자들이 문제 해결 아이디어를 댓글로 달았다.
사실 현대 수학은 수학자 한 명이 혼자서 다 알기가 매우 어렵다. 이미 분야별로 많은 발전을 이뤄서 같은 수학임에도 분야가 다르면 이해하기가 쉽지 않다. 그런데 어떤 문제는 두 분야를 연결하면 쉽게 풀린다. 즉 다양한 분야의 전문가가 힘을 합쳐 연구하면 쉽게 난제를 해결할 수 있을 거라고 여기고 프로젝트를 진행했다.
에르되시 불일치 문제를 해결하기 위해 많은 수학자가 다양한 아이디어를 제시했다. 하지만 좀처럼 쉽게 해결되지 않았다. 타오 교수도 이 문제를 해결하기 위해 댓글을 달며 열성적으로 참여했다.
순식간에 풀려버린 난제
그러던 지난 9월 타오 교수는 아들의 피아노 수업을 기다리다 번뜩이는 아이디어를 떠올렸고, 문제를 해결할 수 있었다. 그렇다면 타오 교수의 아이디어는 무엇일까? 이는 ‘엔트로피’로 설명이 가능하다. 정보이론에서 엔트로피는 얼마나 무작위한지를 나타낸다. 수의 배열이 무질서하면 엔트로피가 크고, 규칙성이 있으면 엔트로피가 작다.
우선 모든 n에 대해 n의 배수번째 수들의 부분합과 0 사이의 차이가 100만 이하가 되도록 1과 -1을 잘 섞어놓을 수 있다고 가정하자. 그리고 1과 -1로 이뤄진 수열을 1번부터 1000번 까지 잘라서 본다. 만약 여기서 어떤 n의 배수번째 부분합과 0 사이의 차이가 100만보다 큰 경우를 찾았다면 가정에 모순이 돼 문제가 해결된다. 만약 찾을 수 없다면, 수열을 더 길게 자르고 1부터 1000번까지 부분의 엔트로피보다 1000번 이후 부분의 엔트로피가 어떤값 이상 차이나게 작다는 것을 증명한다. 이 과정을 계속 반복하면 엔트로피는 점점 작아지지만 0보다 작을 수 없으므로 언젠가 반드시 모순이 생긴다.
타오 교수는 처음 에르되시가 제시한 문제에서 더 나아가 복소수와 무한차원의 힐베르트 공간 위에서도 증명했다. 1과 -1이 오른쪽과 왼쪽을 나타내는 일직선이라면, 복소수에서는 방향을 사방으로 가질 수 있어 원형으로 나타난다. 앞의 만화는 에르되시 불일치 문제를 복소수로 확장한 것이다. 심지어 30km를 훨씬 더 긴 거리로 바꾸더라도 결국 세 명의 수학자가 탈출할 방법이 반드시 있다.
사실 타오 교수의 이번 논문은 여러 검증 절차를 거쳐 유명한 저널에 실린 것이 아니다. 단지 인터넷에 논문을 공개한 것뿐인데, 화제가 되고 있다. 타오 교수가 풀었다면 반드시 답이 맞을 거라는 믿음 때문이다. 조만간 수학 저널의 검증을 거쳐 논문으로 출판될 것으로 보인다. 수학자 출신인 세계적인 갑부 제임스 사이먼스가 가장 부러운 사람으로 타오 교수를 꼽을 만큼 현재 그는 세계 최고의 수학자다. 현대 수학에서는 여러 분야를 두루 섭렵한 수학자가 없는데, 그는 폭넓게 수학 연구를 하고 있다. 타오 교수의 다음 연구 결과가 어떤 것인지 벌써부터 기대가 된다.

과연 타오 교수는 어떤 문제를 풀었을까?
“이 문제를 푼 사람에게는 상금으로 500달러(현재 가치로 약 1천 750만 원)를 주겠습니다.”
83년 전 폴 에르되시는 ‘에르되시 불일치 문제’라는 정수론 문제를 내고 상금을 걸었다. 이후 많은 수학자들이 이 문제에 도전장을 내밀었지만, 번번이 실패하고 말았다. 문제 자체는 그리 어려워 보이지 않았지만, 막상 풀려고 하면 어떻게 문제에 접근해야 할지 막막했기 때문이다.
에르되시 불일치 문제는 1과 -1, 달랑 두 수하고만 관련이 있다. 1과 -1을 골고루 잘 섞은 뒤 길게 늘어놓은 수열이 있다고 하자. 임의의 수 n을 고른 다음 n의 배수번째에 있는 수만을 골라낸다. 이렇게 만든 부분 수열에 1과 -1이 골고루 섞여 있게 할 수 있는지 묻는 문제다. 즉 부분수열의 합(부분합)과 0 사이의 차이를 항상 작게 만들 수 있냐는 것이다. 예를 들어 100만을 기준으로 삼자. 100만보다 큰 부분 수열의 합이 있는지, 혹은 -100만보다 작은 부분 수열의 합이 있는지 묻는 것이다. 있다면 1과 -1이 골고루 섞여 있지 않은 것이다. 부분 수열을 결정하는 수n은 3이나 1000 등 어떤 수도 될 수 있다.
그런데 타오 교수에 의하면 1과 -1이 골고루 섞여 있는 건 불가능하다. 즉 1과 -1을 어떻게 늘어놓아도 적당히 n을 잘 골라서 n의 배수번째 수들을 더해가다 보면 그 부분합과 0 사이의 차이가 100만보다 커지는 순간이 생기는 n을 반드시 찾을 수 있다.

간단한 경우를 살펴보기 위해 기준을 100만 대신 1로 바꾸고, 1과 -1도 원숭이와 양으로 바꿔 생각해 보자. 우선 원숭이와 양 12마리를 잘 나열한다. 모든 n에 대해 n의 배수번째에 나타난 원숭이의 수와 양의 수를 세었을 때 그 차이가 항상 1을 넘지 않게 할 수 있을까? 만약 그림과 같이 나열돼 있다면 3의 배수와 6의 배수에서 양이 2마리 더 많아 골고루 섞여 있지 않다. 하지만 총 11마리가 있다면 모든 부분 수열에서 1을 넘지 않게 만들 수 있다. 즉 골고루 섞이게 배열할 수 있다.
증명만 1만 5000쪽!
여기까지가 불과 몇 년 전까지 알려져 있던 내용이다. 1과 -1을 길게 늘어놓았을 때 앞에서 부터 12개 수만 알면, 거기서 벌써 부분합과 0 사이의 차이가 항상 1보다 크게 할 수 있다. 물론 적당한 n을 잘 골라 n의 배수번째 수들을 더해나갔을 때 말이다. 사실 문제 자체는 중학생도 이해할 수 있을 정도로 그리 어렵지 않다. 하지만 이를 증명하는 것은 매우 어렵다. 이를 단편적으로 보여주는 것이 지난해 2월 발표된 논문이다.
영국 리버풀대 알렉세이 리시차와 보네스 코네브는 적당한 n에 대해 n의 배수번째 수들의 부분합과 0 사이의 차이가 2보다 큰 경우가 반드시 있다는 사실을 증명했다. 이때 전체 수열의 길이가 1161이라고 것도 밝혀냈다. 기준이 1일 때 1과 -1을 12개까지 알아야 했다면, 2일 때는 1161개까지 살펴봐야 한다는 것이다.
연구팀은 논리식을 만들어 컴퓨터로 풀었다. ‘첫 번째가 +1이면 두 번째도 +1, 세 번째는 -1이어야 한다’처럼 여러 가지 경우를 따져 프로그램을 짰다. 그 결과 증명 내용만 13GB에 달했다. 계산 결과만 1만 5000쪽이나 됐다. 위키피디아의 정보량이 10GB정도라고 하니 위키피디아의 정보량보다 증명 분량이 훨씬 많은 셈이다. 즉 획기적인 아이디어 없이 모든 경우를 일일이 따져 문제를 해결하는 건 불가능하다.
함께 풀어야 답이 보인다
그렇다면 이처럼 어려운 문제는 어떻게 해결할 수 있을까? 수학자들은 여럿이서 머리를 맞대야 한다고 생각했다. 그 선두에 1998년 필즈상 수상자인 티머시 가워스 교수가 있다. 2009년말, 그는 에르되시 불일치 문제를 포함한 여러 수학 문제를 온라인에서 함께 풀자고 제안했다. 일명 ‘폴리매스(POLYMATH)’ 프로젝트다. 가워스 교수는 인터넷 사이트를 만들고 수학문제를 소개했다. 그러면 수학자들이 문제 해결 아이디어를 댓글로 달았다.
사실 현대 수학은 수학자 한 명이 혼자서 다 알기가 매우 어렵다. 이미 분야별로 많은 발전을 이뤄서 같은 수학임에도 분야가 다르면 이해하기가 쉽지 않다. 그런데 어떤 문제는 두 분야를 연결하면 쉽게 풀린다. 즉 다양한 분야의 전문가가 힘을 합쳐 연구하면 쉽게 난제를 해결할 수 있을 거라고 여기고 프로젝트를 진행했다.
에르되시 불일치 문제를 해결하기 위해 많은 수학자가 다양한 아이디어를 제시했다. 하지만 좀처럼 쉽게 해결되지 않았다. 타오 교수도 이 문제를 해결하기 위해 댓글을 달며 열성적으로 참여했다.
순식간에 풀려버린 난제
그러던 지난 9월 타오 교수는 아들의 피아노 수업을 기다리다 번뜩이는 아이디어를 떠올렸고, 문제를 해결할 수 있었다. 그렇다면 타오 교수의 아이디어는 무엇일까? 이는 ‘엔트로피’로 설명이 가능하다. 정보이론에서 엔트로피는 얼마나 무작위한지를 나타낸다. 수의 배열이 무질서하면 엔트로피가 크고, 규칙성이 있으면 엔트로피가 작다.
우선 모든 n에 대해 n의 배수번째 수들의 부분합과 0 사이의 차이가 100만 이하가 되도록 1과 -1을 잘 섞어놓을 수 있다고 가정하자. 그리고 1과 -1로 이뤄진 수열을 1번부터 1000번 까지 잘라서 본다. 만약 여기서 어떤 n의 배수번째 부분합과 0 사이의 차이가 100만보다 큰 경우를 찾았다면 가정에 모순이 돼 문제가 해결된다. 만약 찾을 수 없다면, 수열을 더 길게 자르고 1부터 1000번까지 부분의 엔트로피보다 1000번 이후 부분의 엔트로피가 어떤값 이상 차이나게 작다는 것을 증명한다. 이 과정을 계속 반복하면 엔트로피는 점점 작아지지만 0보다 작을 수 없으므로 언젠가 반드시 모순이 생긴다.
타오 교수는 처음 에르되시가 제시한 문제에서 더 나아가 복소수와 무한차원의 힐베르트 공간 위에서도 증명했다. 1과 -1이 오른쪽과 왼쪽을 나타내는 일직선이라면, 복소수에서는 방향을 사방으로 가질 수 있어 원형으로 나타난다. 앞의 만화는 에르되시 불일치 문제를 복소수로 확장한 것이다. 심지어 30km를 훨씬 더 긴 거리로 바꾸더라도 결국 세 명의 수학자가 탈출할 방법이 반드시 있다.
사실 타오 교수의 이번 논문은 여러 검증 절차를 거쳐 유명한 저널에 실린 것이 아니다. 단지 인터넷에 논문을 공개한 것뿐인데, 화제가 되고 있다. 타오 교수가 풀었다면 반드시 답이 맞을 거라는 믿음 때문이다. 조만간 수학 저널의 검증을 거쳐 논문으로 출판될 것으로 보인다. 수학자 출신인 세계적인 갑부 제임스 사이먼스가 가장 부러운 사람으로 타오 교수를 꼽을 만큼 현재 그는 세계 최고의 수학자다. 현대 수학에서는 여러 분야를 두루 섭렵한 수학자가 없는데, 그는 폭넓게 수학 연구를 하고 있다. 타오 교수의 다음 연구 결과가 어떤 것인지 벌써부터 기대가 된다.












