
제1코스 마방진으로 보는 중심육각수, 19
다양한 도형의 형상에 대응시킨 수를 ‘형상수’라고 한다. 형상수에는 삼각형, 사각형 등에 대응시킨 삼각수, 사각수 등이 있다. ‘삼각수’는 점으로 삼각형 모양을 만들었을 때, 사용된 점의 총 개수를 뜻한다. 또한 한 점을 중심으로 점의 수를 늘리면서 정육각형으로 배열할 때 사용된 점의 개수를 ‘중심육각수’라고 한다. 19는 3번째 중심육각수다.
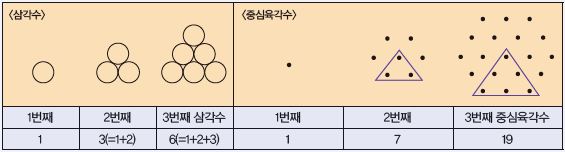
19가 3번째 중심육각수란 사실을 적용해 마방진을 만들어 보자. 19개의 각 점에 1부터 19까지의 자연수를 부여하는데, 각 변에 위치한 3개의 숫자의 합이 모두 같도록 한다. 이 3개의 숫자의 합을 k라고 가정하고 중심육각수의 중심에 놓이는 수를 x, 6개의 꼭짓점에 대응하는 수를 a, b, c, d, e, f라고 하자.


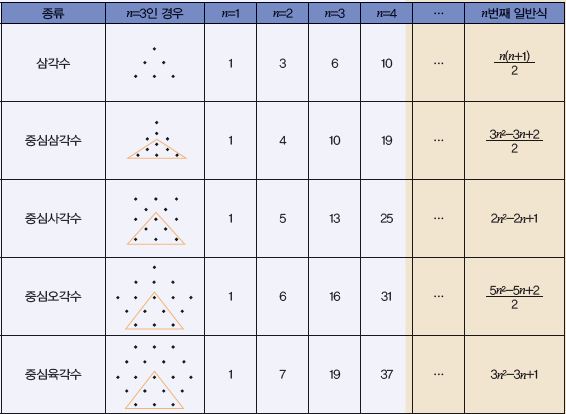
위 표를 유심히 살펴보면 한 가지 재미있는 사실을 또 발견할 수 있다. 7=6×1+1, 19=6×3+1, 37=6×6+1과 같이 n번째 중심육각수는 n-1번째 삼각수의 6배보다 1이 많다는 것이다. 그 이유는 다음 그림을 통해 쉽게 확인할 수 있다.
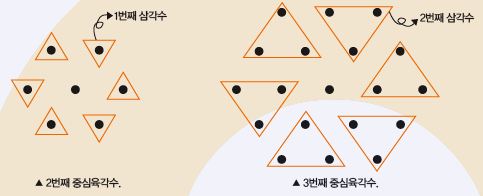
또한 중심육각수를 차례로 더한 수인 1, 1+7, 1+7+19, 1+7+19+37, …을 정리하면 1=1³, 8=2³, 27=3³, 64=4³, …과 같이 자연수의 세제곱수 n³가 되는 것을 확인할 수 있다. 이는 n번째 중심육각수 Hn=3n²-3n+1이 연속한 자연수의 세제곱의 차인 n³-(n-1)³과 같기 때문이다. 1번째~(n-1)번째 중심육각수까지의 합이 (n-1)³이면 Hn=3n²-3n+1=n³-(n-1)³이므로, 1번째~n번째 중심육각수까지의 합은 (n-1)³+{n³-(n-1)³}=n³이 되는 것이다.
중심육각수에 대한 또 다른 재미있는 성질은 수를 나열해 보면 찾아볼 수 있다.
1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919, …

제3코스 19와 배수판정법
이번엔 19의 배수판정법에 대해 알아보자.
19181716151413121110987654321은 19의 배수일까? 아닐까? 물론 19로 직접 나누어 보는 것도 좋은 방법이지만, 좀 다른 방법을 써 보도록 하자. 먼저 19의 배수의 특징을 살펴보자.
다음 세 자연수는 모두 19의 배수다.
19, 152, 3819
그런데 신기하게도 일의 자리의 수를 2배한 뒤, 일의 자리 앞에 놓인 수를 더하는 작업을 계속하면 언제나 19가 나온다.
19 → 1+2×9=19
152 → 15+2×2=19
3819 → 381+2×9=399 → 39+2×9=57 → 5+2×7=19
왜 이런 성질이 나타나는 것일까? 그 이유를 알아보기 위해 우선 일의 자리의 수가 b인 자연수 A를 10a+b라고 하자. 그런데 10a+b=19a+19b-9a-18b=19(a+b)-9(a+2b)이므로 좌변의 10a+b가 19의 배수이면 우변의 19(a+b)-9(a+2b)도 19의 배수다. 이때, 19(a+b)는 19의 배수이므로 9(a+2b)도 19의 배수가 돼야 하고, 19는 소수이므로 a+2b도 소수가 돼야 한다.
따라서 어떤 자연수가 19의 배수인지 아닌지를 알아보려면 그 자연수의 일의자리의 수를 2배한 뒤, 일의자리의 수 앞에 놓인 수에 더한 수가 19의 배수인지를 확인하면 된다.

이 방법을 이용하면 앞에서 소개한 자연수 19부터 연속한 자연수 19개를 이어서 만든 자연수19181716151413121110987654321도 19의 배수라는 것을 알 수 있다. 아쉽게도 직접 19로 나누어 보는 방법보다 편리하다고 할 수는 없지만, 자신의 계산 실력도 확인할 겸 위와 같은 방법으로 19의 배수를 확인해 보도록 하자.
이와 같은 원리를 바탕으로 하는 배수 판정법은 19 외에 다른 수에도 쉽게 적용할 수 있다는 장점이 있다. 예를 들어 7의 배수에 이 방법을 적용해 보자. 이전과 같이 일의 자리의 수가 b인 자연수 A를 10a+b라 하고, 위와 같이 식을 변형하면 다음과 같다.
10a+b=7a+7b+3a-6b=7(a+b)+3(a-2b)
따라서 A가 7의 배수이면 아래 식에서 a-2b가 7의 배수가 돼야 한다. 이처럼 k의 배수에 어떤 수를 더해도 k의 배수가 되려면, 어떤 수 역시 k의 배수가 돼야 한다는 원리를 이용한 배수의 판정법을 ‘스펜스의 방법’이라고 한다.
19는 19개의 네제곱수의 합으로 나타낼 수 있는 559, 마방진과도 접목되는 세 번째 중심 육각수 19, 바둑에 담겨 있는 19 등 생각보다 아주 많은 곳에서 제 몫을 다하고 있다. 19처럼 여러분도 자신이 위치한 곳에서 최선을 다하는 자세로 2012년의 12월을 마무리하도록 하자. 이번 달을 마지막으로 숫자이야기는 막을 내린다. 19와 같이 기대보다 더 알찬 다음 만남을 기약하면서, 그동안 숫자 여행을 함께 해온 독자들에게 아쉽지만 마지막 인사를 전한다.












