“아이쿠, 우리 두리가 정말 만들고 싶었나 보구나. 하지만 처음부터 저런 구조물을 만들긴 쉽지 않을 텐데. 먼저 아빠랑 종이로 만든 다면체를 만들어 보면 어떨까?”
축구공을 닮은 다면체, 깎은 정이십면체

올해는 대한민국 전 국민을 하나가 되게 했던 2002년 한일월드컵이 열린 지 10년이 되는 해다. 축구 경기에서 빼놓을 수 없는 축구공은 오랜 시간을 거듭하면서 다양한 모양으로 진화했다. 축구공은 다면체를 닮아 입체도형을 이해하기에 좋다.
4년마다 열리는 월드컵에서는 그 월드컵에서 사용하는 공인구를 발표한다. 그 중에서도 1970년 멕시코월드컵의 공인구 ‘텔스타’는 아르키메데스의 다면체 중 하나인 ‘깎은 정이십면체’ 모양으로 만들었다.
아르키메데스의 다면체란, 두 종류 이상의 정다면체로 이뤄져 있으면서 꼭짓점에 모인 면의 배치가 서로 같은 볼록다면체를 뜻한다. 준정다면체라고도 불리는 아르키메데스의 다면체는 모두 13가지 종류가 있다.

그렇다면 텔스타와 모양이 같은 깎은 정이십면체는 어떻게 만들 수 있을까? 가장 쉽게 만들 수 있는 방법은 다면체 전개도를 이용하는 것이다. 왼쪽 그림과 같이 정오각형과 정육각형으로 이뤄진 전개도를 오린 다음, 날개를 붙이면 깎은 정이십면체를 만들 수 있다.
전개도를 이용하지 않고 다면체를 만들 수도 있다. 같은 모양의 종이를 풀로 붙이지 않고 끼워 만드는 방법으로, 전개도를 이용해 다면체를 만드는 방법보다는 좀 더 생각하는 과정이 필요하다. 다면체를 이루는 면을 어떤 모양으로 할지, 종이는 어떻게 끼워야 할지 결정해야 하기 때문이다.
예를 들어 축구공 텔스타의 모양인 깎은 정이십면체는 정삼각형 종이 20장을 이용해 끼워 만들 수 있다. 정삼각형의 세 변에 홈을 만들어 종이를 서로 끼우면 정육각형 면이 생기고, 또 5장을 서로 연결하면 정오각형 면을 만들 수 있어 두 가지를 이용해 깎은 정십이면체를 만들 수 있다. 이제 <;실험1>;을 통해 종이를 끼워 만든 축구공을 직접 만들어 보자.
아하! 생각이 쑥쑥! 다면체에서 찾아보는 점, 선, 면!
<;실험1>;과 <;실험2>;를 통해 만든 다면체가 전개도를 이용해 만든 다면체와 다른 점은 뭘까? 합동인 평면도형을 여러 장 이용해 끼워 만든다는 점이다. 덕분에 전개도를 이용해 만드는 것보다 방법이 어렵고, 시간도 오래 걸린다.
그렇지만 종이를 끼워 입체도형을 만들면 전개도로 만들 때보다 입체도형이 완성되는 과정을 좀 더 자세하게 살펴볼 수 있다. 만드는 과정에서 자연스럽게 입체도형을 구성하는 점, 선, 면을 찾고 입체도형의 구조를 익힐 수도 있다. 특히 종이를 끼워 만든 입체도형은 바깥으로 종이가 나와 있어, 평면과 평면이 만나 이루는 모서리를 선명하게 볼 수 있다.
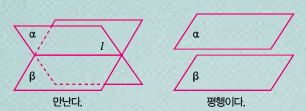
공간에서 두 평면이 갖는 위치의 종류는 만나거나, 평행하는 위치로 두 가지뿐이다. 여기서 두 평면이 만나는 경우에는 반드시 만나는 직선이 생기는데, 이 직선을 ‘교선’이라고 부른다. 종이를 끼워 만든 다면체에서 합동인 종이를 한 평면으로 보면, 다면체를 이루는 모든 모서리는 평면과 평면이 만나 생기는 교선이 된다.
그렇다면, 공간에서 두 직선의 위치 관계는 몇 종류가 있을까? 공간에서 생기는 직선의 위치관계는 다음과 같이 3가지 경우가 있다. 여기서 두 직선이 ‘꼬인 위치’에 있다는 것은, 한 점에서 만나지도 않고 평행하지도 않은 경우를 말한다.

이제 종이를 끼워 만든 다면체를 이용해 서로 만나는 평면과 평행인 평면을 찾아보자. 또 서로 만나거나 평행인 직선은 물론, 꼬인 위치에 있는 직선도 찾아보자. 어느새 입체도형의 달인이 된 자신을 발견하게 될 것이다.