d라이브러리

학생들의 답안을 채점하다 보면 때때로, 어떤 조건을 만족시키는 예가 존재한다거나 혹은 존재하지 않음을 수학적이지 않은 논리에 호소하는 부주의한 주장을 만나게 됩니다. 그러나, 굉장히 존재하기 힘들 것 같은 느낌을 주는 예가 실은 존재할 때가 있습니다. 그런 상황을 묻는 문제도 가끔씩은 등장하는데, 그런 문제들을 아래에 준비해보았습니다. 이런 문제를 만나봄으로써, 부주의한 풀이를 적어내던 일부 학생들이 앞으로는 좀 더 확실한 논리를 찾는 노력을 하게 되기를 기대합니다.


➊ 도시대항 국제수학토너먼트(TOT) 1982년 가을 고등부 2번

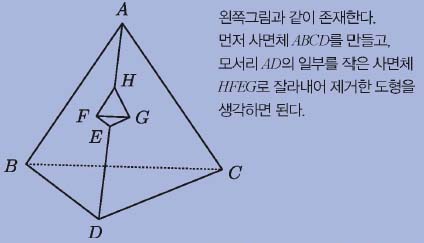
각 꼭짓점의 연결관계만을 펼쳐 나타내었을 때, 다음 그림과 같이 AB, AC, BC, BD, CD, DE, EF, EG, FG, FH, GH, AH의 12개의 모서리를 갖는 (굳이 볼록일 필요는 없는) 다면체가 존재하는가?
 

이런 다면체가 잘 없을 것 같은 느낌이 들겠지만, 실례가 없음을 증명하는 것보다는 희귀하더라도 실례 하나를 찾아내는 것이 훨씬 쉬운 풀이가 되기 마련입니다. 그럼 당연히 실례가 있을지 찾아보려는 노력을 실례가 없음을 증명하려는 노력보다 먼저 밟아보는 것이 순리입니다. 실례를 찾아보려는 충분한 노력의 끝에서 비로소 실례가 존재할 수 없는 이유의 힌트가 발견되면, 그것을 바탕으로 불가능성을 명쾌하게 수학적인 논리로 논하는 풀이를 찾아내야 합니다.

이 문제의 경우에는 오목다면체도 열심히 생각해보면 실례가 존재합니다.


고봉균 선생님의 풀이
 

➋ 도시대항 국제수학토너먼트(TOT) 1984년 봄 중등부 A레벨 4번

직각이등변삼각형을 그것과 닮은 서로 다른 크기의 유한개의 삼각형으로 쪼갤 수 있는가?

이웃하는 조각끼리 변과 변이 정확히 일치하는 분할만 생각하기 쉽고, 그럼 아무리 쪼개도 같은 상황이 계속 반복되면서 똑같은 크기의 삼각형이 항상 둘이 남게 됩니다. 두 변 이상이 모여 다른 조각의한 변이 되는 그림을 찾아내야겠다는 생각이 필요합니다.


고봉균 선생님의 풀이