d라이브러리

여러 형태의 도형 타일을 이용해서 이런저런 모양을 만들어보는 놀이를 어렸을 때 했던 기억이 있나요?
이번에 소개할 주제는 그런 놀이와 관련된 것입니다. 아주 쉬운 문제에서부터 아주 어려운 문제까지
이어집니다. 특히, 쉬운 문제들을 쌓아서 아주 어려워 보이던 문제를 해결하는 기쁨도 발견할 수
있습니다. KAIST 사이버영재교육센터에서 2004년에 출제되었던 과제입니다.

이번 과제에 대한 맛보기로 먼저 다음의 그림 맞추기 퍼즐들을 풀어보자.

문제1
 

(1) 같은 크기의 2개의 정사각형을 몇 개의 조각으로 적당히 자른 후 그것들을 조립하여 원래 정사각형의 2배의 넓이를 갖는 새로운 정사각형을 하나 만들어라.
 

(2) 삼각형 ABC에서 변 BC의 중점을 D라 하면 두 삼각형 ABD와 ACD는 같은 넓이를 가진다. 삼각형 ABD를 두 조각으로 잘라 다시 붙여 삼각형 ACD를 만들어라.
 

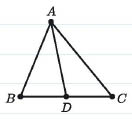
(3) 같은 크기의 정사각형 5개를 붙여서 만든 십(+)자 모양의 12각형을 생각하자. 이 십자꼴 12각형을 10개 이하의 작은 다각형 조각으로 잘라 이 도형과 같은 넓이의 정사각형 하나를 만들어라.
 

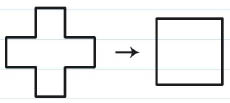
(4) 같은 크기의 3개의 정삼각형을 몇 개의 조각으로 적당히 자른 후 그것들을 조립하여 원래 정삼각형의 3배의 넓이를 갖는 새로운 정삼각형을 하나 만들어라.
 

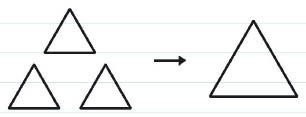
(5) 정삼각형을 10개 이하의 조각으로 잘라서 원래 정삼각형과 같은 넓이를 갖는 정사각형을 만들어라.
이번 과제에서는 다각형의 분할과 조립에 관련하여 1830년대에 증명된 다음의 명제를 함께 되짚어보고자 한다.
 

정리
넓이가 같은 임의의 두 다각형 A와 B에 대해, 다각형 A를 유한개의 작은 다각형으로 자른 후 그 조각들을 다시 잘 모아 다각형 B를 만드는 것이 항상 가능하다.

매우 흥미로운 사실이기는 하지만, 한편 두려운 느낌이 들지도 모르겠다. ‘과연 이런 문제를 우리가 풀 수 있을까?’ 하는…. 그냥 이대로라면 어디에서부터 무엇을 생각해야 할지 막막하겠지만, 이곳의 과제는 여러분에게 늘 좋은 안내를 제공한다. 다음의 문제들을 하나씩 풀어 가다 보면 어려워만 보이던 저 명제
의 해법에 차차 접근할 수 있을 것이다.

문제2

(1) 임의로 주어진 삼각형을 두 조각으로 잘라 원래의 삼각형과 같은 넓이의 평행사변형으로 조립할 수 있음을 보여라.

(2) 임의로 주어진 삼각형을 세 조각으로 잘라 원래의 삼각형과 같은 넓이의 직사각형으로 조립할 수 있음을보여라.



문제3

임의로 주어진 직사각형을 유한개의 작은 다각형 조각으로 잘라 원래의 직사각형과 같은 넓이의 정사
각형으로 조립할 수 있음을 보여라.

두 종류의 정사각형 타일로 평면을 가득 까는 것을 생각하자. 하나의 작은 타일 주위를 네 개의 큰 타일이 둘러싸듯 하며 두 종류의 타일을 번갈아 깔 수 있다.
 

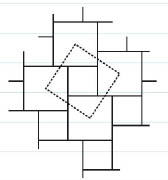
여기서 하나의 작은 타일 주위를 둘러싼 네 타일의 중심점들을 차례로 연결하면 정사각형이 되는데, 그 넓이는 피타고라스의 정리 a²+b²=c²에 의해 처음 두 정사각형의 넓이의 합이 된다. 이것은 다음 문제의 힌트가 된다.

문제4

임의의 두 정사각형 A와 B에 대해, 이들을 유한개의 작은 다각형 조각으로 잘라, 두 정사각형의 넓이를 합한 것과 같은 넓이를 갖는 정사각형으로 조립할 수 있음을 보여라.

이제 거의 준비가 다 되어 간다. 다음의 문제를 풀 때에는 오목한 부분이 있는 다각형도 있다는 것을 잊지 말자.

문제5

임의의 다각형을 항상 유한개의 작은 삼각형들로 쪼갤 수 있음을 보여라.

이제 준비가 다 되었다. 앞의 문제들을 이용해 우리가 원하던 정리를 완성해보자. 앞의 문제들에서 말하는 사실 중에 자신이 풀지 못한 것이 있더라도 다음의 문제들을 푸는 데에 이용해도 좋다.

문제6

(1) 임의의 다각형을 유한개의 작은 다각형으로 자른 후 그 조각들을 다시 잘 모아 원래의 다각형과 같은 넓이의 정사각형으로 조립할 수 있음을 보여라.

(2) 넓이가 같은 임의의 두 다각형 A와 B에 대해, 다각형 A를 유한개의 작은 다각형으로 자른 후 그 조각들을 다시 잘 모아 다각형 B를 만들 수 있음을 보여라.

이것으로 원하던 정리를 증명할 수 있었다. 막막해만 보이던 문제가 정사각형을 매개로 하여 멋지게 풀렸다. 정사각형을 매개로 사용한 것은 다른 도형보다 다루기 쉽다고 여겨지기 때문이다. 정사각형 대신 정삼각형 등 다른 도형을 매개로 하는 해법을 생각해보는 것도 재미있을지 모른다.