d라이브러리

한 문제를 푸는 방법이 늘 한 가지만 있는 것은 아닙니다. 이번에는 그런, 전혀 다른 두 가지 아이디어로 풀리는 문제를 만나보려고 합니다.

도시대항 국제수학토너먼트(TOT) 2001년 가을 A레벨 중등부 2번

n≥3은 자연수이다. 한 원의 둘레가 2n개의 점에 의해 2n개의 원호로 분할되어 있다. 각 호의 길이는세 종류뿐이고 이웃한 두 호의 길이는 항상 서로 다르다. 2n개의 점을 차례로 번갈아 빨강과 파랑으로 색칠하였다. 빨간 점으로 된 n각형과 파란 점으로 된 n각형은 둘레의 길이도 같고 넓이도 같음을 증명하여라.
 

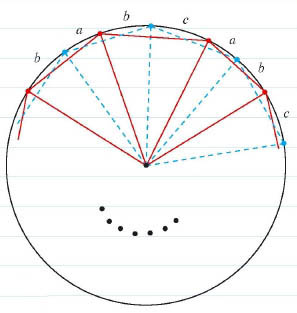
우선 생각할 수 있는 것은, 빨간 변의 길이들을 모두 모은 것과 파란 변의 길이들을 모두 모은 것이 집합적으로 일치하지 않을까(*) 하는 것입니다. 만일 그렇다면 둘레의 길이가 같음은 바로 확인되고,원의 중심에서 각각의 꼭짓점을 연결한 이등변삼각형으로 쪼개는 것을 생각하면 이 이등변삼각형들의모임 역시 빨간 다각형에서와 파란 다각형에서 서로 집합적으로 일치하므로, 총넓이가 같음도 알 수 있습니다. 따라서, (*)만 보이도록 하겠습니다.



고봉균 선생님의 풀이②

연속한 세 호의 길이가 …, a, b, a, …꼴인 부분(한 호의 양옆 길이가 같은 부분)이 있으면 거기서 a, b를 하나씩 줄여서 생각해도 된다. (양쪽 다각형에서 호의 길이가 a+b인 변이 하나씩 제거된다.) 그런 식으로 상쇄시켜가다 보면, 언젠가 …, a, b, a, …꼴이 하나도 남지 않게 되는 순간이 올 것이다. 그 순간에는 …, a, b, c, a, b, c, …의 순서로 계속 순환 반복된다. (a, b 다음에는 a도 b도 올 수 없으므로 c가 올 수밖에 없고, 이런 식으로 같은 논리가 반복된다.) 짝수 개의 원호로 이루어져 있으므로, (a, b, c)패턴도 짝수 개이고, 그럼 호의 길이가 a+b인 변은 양쪽 다각형에 한 번씩 번갈아 포함되어 결국 같은 개수가 된다. 다른 종류의 변들도 마찬가지이고, 따라서 앞의 풀이에서처럼변의 길이들의 모임이 집합적으로 일치하므로 문제가 증명된다.