d라이브러리

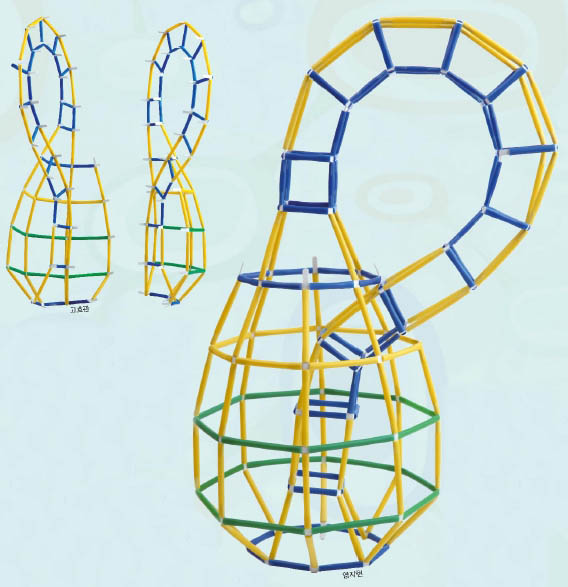
“클라인병은 뫼비우스 띠 2개로 구성돼 있습니다”

지난 4월 16일 미국 인디애나폴리스에서 열린 미국수학교육컨퍼런스에서 4D창의연구소 박호걸 소장은 4D프레임을 활용해 클라인병의 성질을 확인하는 방법에 대해 강연했다. 미국수학교육컨퍼런스는 미국수학교사협의회(NCTM)가 주관하는 가장 큰 행사로 매년 전 세계 수학교육종사자 8000~9000명이 참가한다. NCTM은 미국수학교육에 종사하는 사람들의 모임으로 1929년 만들어진 이래 세계 수학교육의 흐름과 변화를 주도하고 있다. NCTM에서 발행한 지침서 ‘수학교육과정 및 평가기준’ 은 전 세계 수학교육 교재에 인용될 정도로 세계 수학교육에 영향력이 크다.
 

4D창의연구소는 4월 11일부터 6일 동안 열린 이번 컨퍼런스에 전시부스를 마련해 4D프레임으로 만든 다양한 수학구조물을 전시했고 관람객이 직접 거품장력실험을 할 수 있도록 했다. 거품장력실험은 4D프레임으로 만든 다면체를 비눗물에 담갔다 꺼내 다면체에 생기는 비누거품 막을 관찰하는 실험이다.

컨퍼런스 마지막 날 박 소장은 강연 중에 수학교육자 40명과 클라인병 모형을 만들었다. 클라인병은 병의 안과 밖을 구별할 수 없는병으로 독일의 수학자 펠릭스 클라인이 고안했다.

수학적으로 특이한 성질을 가진 클라인병은 일반적인 3차원 공간에서 만들어지지 않는다. 그래서 3D프로그램을 이용해 컴퓨터로 모형을 보여주는 것이 전부였다. 그러나 빨대 모양의 4D프레임 연결봉은쉽게 구부러지는 성질이 있어 안과 밖이 구별되지 않는 클라인병 모형을 만들 수 있다. 물론 완벽한 클라인병은 아니다.

강연에 참여한 교사들과 클라인병 모형을 만든 박 소장은 자신이 만든 모형을 분해하기 시작했다. 이 병을 정확하게 세로로 반으로 나누면 2개의 뫼비우스 띠가 되는 것을 확인하기 위해서다.

박 소장은 “말이나 글로만 설명하면 학생들은 이해하지 못한다” 며 “4D프레임은 연결봉을 풀기도 쉬워 클라인병 모형을 분해하면 뫼비우스 띠 2개를 볼 수 있다” 고 설명했다.

강연에 참가한 정인숙 미국 노르트담 세인트메리대 교육학과 교수는 “미국은 현재 여러 과목을 함께가르치는 통합교육을 어떻게 할지 고민하고 있다” 며 “4D프레임은 기하와 물리를 함께 가르칠 수 있어 좋다” 고 평가했다. 정 교수는 또 “4D프레임은 수학 수업에 흥미와 동기를 유발하고 창의력을 계발하는 데 좋은 교구” 라고 덧붙였다.

4D프레임을 활용한 수학 수업방법은 국내 연구진에 의해 개발되고 있다. 현재 3~4편의 논문이 나왔으며, 진행 중인 논문도 여러 건이다. 스웨덴 칼스타드대 교육공학팀과 논문을 진행 중인 황홍택 금오공대 수학과 교수는 “기존의 수학교구는 이미 알려진 수학구조물을 따라 만드는 데 그치지만 4D프레임은 유연성이 있어 새로운 패턴이나 구조물을 만들 수 있는 장점이 있다” 며 “초·중학생들이 4D프레임을 이용해 창의적인 구조물을 만들 수 있는 방법을 연구한다” 고 밝혔다.