‘말하는 수학’은 이야기와 함께 떠나는 수학여행이에요. 이야기 속에 숨어 있는 수학 문제를 선생님과 우리 친구들이 서로 대화하며 풀어가는 코너랍니다. 도란도란 이야기를 나누는 사이에 문제가 하나둘 풀리는 기쁨을 느낄 수 있을 거예요. 자~, 지금부터 소곤소곤 대화방을 열어 볼까요?
미래도시 극복기
여기는 미래도시에 세워진 최신식 학교. 모든 시설이 갖춰졌으나 미래도시의 최대 단점인 공기오염 문제를 해결하지 못했으니…. 나잘난 박사는 이 학교의 공기오염 문제를 해결할 최첨단 공기정화장치를 개발해 학교를 찾았다. 3000명 학생의 목숨이 나잘난 박사의 발명품에 달려 있는 급박한 상황! 과연 나 박사의 발명품이 학생들의 생명을 지킬 수 있는지 확인해 보자.
교장선생님 : 나잘난 박사님! 정말 수고 많으셨습니다. 박사님의 발명품에 우리 학교의 사활이 걸려 있습니다. 박사님이 만드신 공기정화장치의 성능을 소개해 주시지요.
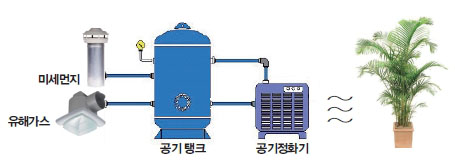
나잘난 박사 : 에~, 이 공기정화기는 외부에서 들어오는 모든 공기를 모으는 탱크와 연결돼 있습니다. 미세먼지와 각종 유해가스가 탱크에 모이기 시작하면 공기정화기도 작동하지요. 공기정화기는 더러운 공기를 깨끗한 공기로 바꿔 학교 전체에 신선한 공기를 제공합니다. 에헴!
교장선생님 : 혹시 정화할 수 있는 용량을 넘는 오염물질이 탱크 안으로 들어오면 어떤 일이 벌어질까요?
나잘난 박사 : 그렇게 되면 탱크 밖으로 오염물질이 새어나와 학생들이 호흡곤란을 일으키겠지만…. 그럴 일은 절대 없습니다! 공기정화기의 용량을 충분히 크게 만들었거든요.
교장선생님 : 아…, 물론 그러시겠지요. 그럼 계속 설명해 주세요.
나잘난 박사 : 매일 같은 양의 오염물질이 탱크에 들어온다고 했을 때, 미세먼지는 5일 만에 탱크를 가득 채웁니다. 각종 유해가스의 경우 4일 만에 탱크가 가득 차게 되지요. 그러나 걱정 없습니다. 이 공기정화기는 탱크 안에 있는 오염물질을 단 3일 만에 모두 정화할 수 있답니다. 껄껄껄~.
교장선생님 : 와우~, 대단하군요. 단 3일 만에 정화시킨다니. 박사님 수고하셨습니다. 당장 계약하도록 하죠.
자~, 여러분의 생각은 어떤가요? 이 공기정화장치는 과연 미세먼지와 각종 유해가스를 말끔히 처리할 수 있을까요? 우리 함께 박사님의 발명품을 꼼꼼히 살펴보도록 해요.
선생님 : 여러분은 이 공기정화장치가 안전하다고 생각하나요?
사랑 : 안전하려면 공기정화기가 작동된 뒤 탱크에 오염물질이 남아 있으면 안 될 것 같아요.
선생님 : 옳은 지적이에요. 그렇다면 이 탱크에서 하루 사이에 일어나는 일들을 확인해 볼 필요가 있겠군요. 하루에 탱크 안으로 들어오는 오염물질의 양은 얼마나 될까요?
선생님 : 그렇다면 공기정화기가 하루에 정화할 수 있는 오염물질의 양은 얼마나 될까요?
선생님 : 그럼 하루에 이 공기정화장치가 오염물질을 완벽히 정화할 수 있는지 어떻게 알 수 있을까요?
선생님 : 계산해 볼까요? 분모가 모두 다르니까 하나의 분모로 통분해야겠군요.
선생님 : 이런…, 큰일 날 뻔했군요. 이 공기정화장치는 박사님의 말처럼 완벽한 게 아니었어요. 그렇다면 이 탱크가 꽉 차서 오염물질이 밖으로 새어나가려면 며칠이 걸리는지 계산해 봐요.
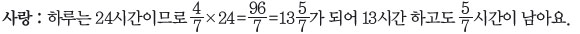
선생님 : 아하~, 8일하고 13시간이면 탱크가 폭발한다는 얘기군요. 좀 더 정확히 분 단위 까지 계산해 봅시다.
선생님 : 마지막으로 초까지 계산해 볼까요?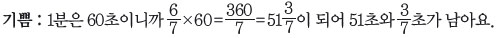

사랑 : 8일하고 13시간 42분 52초면 학생들의 목숨이 위태로울 수 있습니다.
선생님 : 이런 치명적인 결함이 발견되다니…, 어서 교장선생님께 말씀 드리러 갑시다!
여러분~, 이처럼 끔찍한 재앙을 미리 피할 수 있게 된 것은 여러분이 분수를 계산하는 방법을 배운 덕분이랍니다.
디오판토스의 나이를 구하라
그리스의 수학자 디오판토스의 묘비에는 유명한 문제가 새겨져 있어요. 이 문제는 미지수 x를 이용한 방정식으로 많이 푸는데 오늘은 분수만 써서 풀어 보기로 해요. 묘비에 새겨진 글을 읽고 디오판토스의 나이를 함께 맞혀 볼까요?
선생님: 문제를 풀기 위해 먼저 그의 일생을 표로 정리해 봐요.
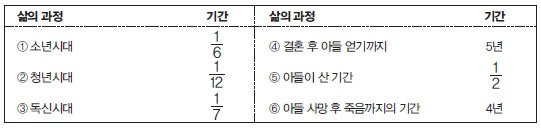
.
.
.
.
.
<;정답>; 디오판토스의 일생을 ‘1’로 두면 9년은 1에서 2528를 뺀 328이 돼요.