d라이브러리

“1등만 기억하는 더러운 세상.”


개그콘서트에 처음 등장한 이 말은 1등만 강요하는 세태를 통렬하게 비판해 크게 유행했다. 하지만 1등에 대한 반감은 잠시 접어두자. 만약 선거에 나간다면 1등을 해야만 한다.


선거는 방법에 따라 결과가 완전히 달라질 수 있다. 학생이 40명인 어떤 학급에서 대표를 뽑기 위해 A, B, C, D에 대해 선호도를 조사한 결과가 다음과 같다고 가정해보자. 이 학급이 최다득표제를 따르면, 1위 표를 가장 많이 받은 A가 당선된다.








‘투표의 역설’ 없는 쌍대비교법


하지만 득표수가 과반이어야 한다는 규칙도 있다면, 40표 중 18표를 얻은 A는 당선자가 될 수 없다. 나머지 22명 중 21명은 A를 4위로 뽑았기 때문에 A가 전반적인 지지를 받는다고 보기 어렵다는 얘기다. 이처럼 최다득표제는 한 번의 투표로 당선자를 가릴 수 있지만, 과반에 못 미치는 지지율로 당선자가 결정되기도 한다. 특히 여러 후보가 난립하면 다수의 유권자가 싫어하는 후보가 당선될 수 있다.


보르다 점수법은 유권자의 선호 순위에 따라 점수를 준 뒤 합산해, 가장 높은 점수를 얻은 후보를 선출하는 방법이다. 프랑스의 정치이론가이자 수학자인 보르다(Jean-Charles de Borda, 1733~1799년)가 프랑스 대혁명기에 제안한 방법으로, 불합리한 구제도(앙시앵 레짐)를 타파하고 정당한 시민의 권리를 찾고자 한 프랑스의 질풍노도가 선거제 개선으로 이어진 경우다. 이 선거법에 따라 1, 2, 3, 4순위에 각각 4, 3, 2, 1점을 주면 최고점을 받은 C가 당선된다. 순위별로 부여하는 점수의 간격이 같다면 점수를 어떻게 정하더라도 순위는 바뀌지 않는다.











그러나 이 방법도 최다득표제보다 꼭 합리적이지는 않다. 선거의 합리성을 따지는 ‘과반수 기준’이란 최다득표를 한 후보자의 표가 만약 과반이면 그 후보자가 반드시 당선돼야 한다는 성질이다. 가령 A, B, C에 대한 투표 결과가 다음 페이지 그림과 같을 때 보르다 점수법을 적용하면 B가 당선되는데, A는 15명 중 과반인 8명으로부터 1위 표를 받고도 당선되지 못한 것이다. 반면 최다득표제는 가장 많은 득표수가 동시에 과반이라면 무조건 그 후보자가 당선된다.


이처럼 선거가 유권자의 선호도를 정확히 반영하지 못하는 현상을 ‘콩도르세 역설’, 혹은 ‘투표의 역설’이라고 한다. 가령 A, B, C 세후보에 대해 유권자가 A를 B보다 선호하고 B를 C보다 선호하면 결국 A를 C보다 선호할 것 같은데, 그렇지 못한 경우가 나타난다는 말이다. 프랑스의 철학자이자 수학자인 콩도르세(Nicolas de Condorcet, 1743~1794년)는 이런 역설이 발생하지 않는 ‘쌍대비교법’을 제안했다.


쌍대비교법은 두 후보씩 비교해 우세한 후보에 점수를 준 뒤 이를 합산해, 최종적으로 가장 높은 점수를 얻은 후보를 선출하는 방법이다. 학급 대표를 선출할 때 우선 두 후보씩 짝을 짓고 동일한 지지를 얻으면 각각에게 0.5점을, 한쪽이 더 많은 지지를 얻으면 그 후보에게 1점을 준다. 점수를 합산해 보면 결국 B가 최종 당선된다.









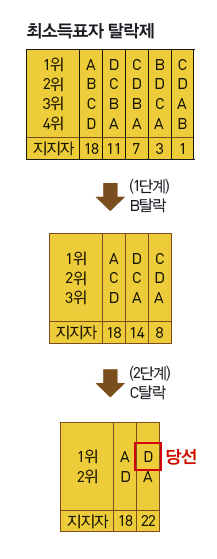
두 후보자씩 비교할 때 다른 후보보다 선호되는 후보자가 당선돼야 한다는 ‘콩도르세 기준’은 다른 선거법의 합리성을 따질 때도 적용된다. 쌍대비교법으로 선출된 B는 콩도르세 기준을 만족하지만, 최다득표제와 보르다 점수법으로 선출된 A와 C는 이 기준을 만족하지 못하는 셈이다. 호주 의회와 미국 시 의회, 인도와 아일랜드 대통령 선거에서 이용하는 ‘최소득표자 탈락제’도 같은 결함을 갖고 있다. 최종 당선자가 두번째로 1위 표가 많았던 D가 되기 때문이다.


A에게 유리하게 바꿨는데, A가 탈락했다?


최소득표자 탈락제는 1위 표를 가장 적게 받은 후보를 탈락시키고 투표 결과를 재정산해 또다시 최소득표자를 탈락시키는 과정을 마지막 한 명이 남을 때까지 반복하는 방법이다. 이 예시에서는 선호하는 후보를 순서대로 적게 했기 때문에 꼴찌 후보를 탈락시키면서 순위를 재산정하는 과정을 반복할 수 있다. 하지만 만약 투표할 때 선호 후보를 한 명만 표시하게 하면 최소득표자를 제외한 뒤 다시 투표해야 한다.


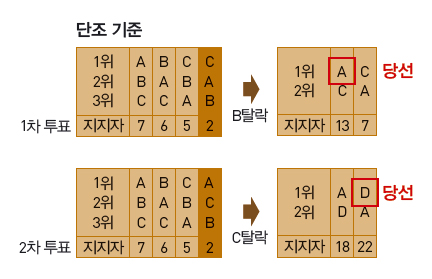
얼핏 공정해 보이지만 최소득표자 탈락제는 콩도르세 기준은 물론 당선자가 정해졌을 때 당선자에 유리하도록 선호도를 바꿔 재투표해도 당선자가 바뀌지 않아야 한다는 ‘단조 기준’을 만족시키지 못한다. 가령 세 후보 A, B, C에 대한 유권자 20명의 선호도 투표 결과가 아래와 같을 때, A, B, C는 1위 표를 각각 7, 6, 7장 받았기 때문에 B가 배제된다. A와 C만 놓고 다시 정리하면 결국 당선자는 A가 된다. 만약 이 때 어떤 사정이 있어서 재투표를 하게 됐는데, 이미 A가 대세라고 생각한 C의 지지자 중 2명이 지지 순위를 C, A, B에서 A, C, B로 바꿨다면(표의 음영 부분) 최종 당선자는 D가 된다. 즉 원래 당선자인 A에 유리하도록 투표 결과를 바꿨는데도 당선자가 A에서 D로 바뀌게 된다!


선거법의 합리성을 판단하는 마지막 기준인 ‘사퇴자 무관’은 낙선자 중 한 명이 사퇴했을 때 그 낙선자를 제외하고 산정해도 당선자가 바뀌지 않는 성질로, 앞서 소개한 네 가지 선거법 모두 이 기준을 충족시키지 못한다. 가령 투표 결과가 다음과 같을 때 쌍대비교법을 적용하면, 원래 당선자는 A인데 후보 D가 중간에 사퇴할 경우 당선자는 B로 바뀐다.










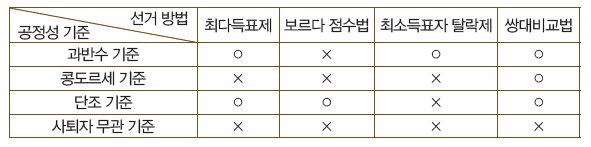
결국 네 선거법을 네 가지 평가 기준에 따라 정리하면, 쌍대비교법은 세 기준에서 합격인 데 비해 최소득표자 탈락제와 보르다 점수법은 오직 한 가지 기준만 충족시킨다. 우리가 보편적으로 사용하는 최다득표제는 두 가지 기준에서 합리적이다.


실망했는가? 하지만 이런 결과가 의외는 아니다. 미국의 경제학자 케네스 애로(Kenneth Arrow, 1921~)는 박사 학위 논문과 1951년 저서 ‘사회적 선택과 개인의 가치’를 통해 후보자가 세 명 이상인 선거에서 철저히 민주적이고 공정한 방법은 수학적으로 존재하지 않는다는 ‘애로의 불가능 정리’를 제시했다. 그 공로로 1972년 노벨 경제학상을 받았다. 영국 플리머스대 마이클 스래셔(Michael Thrasher) 교수는 “특정 선거제도가 완벽하다는 주장은 틀렸다”며 “수학적으로 완벽한 선거제도를 찾기보다 상황에 따라 어떤 선거제도를 이용할지 고려해야 한다”고 주장했다.


민주주의의 꽃이라 불리는 선거. 그 어떤 선거 방법도 공정성 기준에 합격하지 못한다는 점이 다소 실망스럽다. 이처럼 선거 방법이 원천적으로 완벽하지 못하다는 점을 감안한다면 특정 선거 방법에 의해 1등을 한 사람은 불완전하고 잠정적인 당선자일 뿐이다. 따라서 당선자는 조금 더 겸손한 마음을 갖고 자신을 지지하지 않은 다수의 의견에 귀를 여는 대승적인 화합의 모습을 보여주어야 하지 않을까.