d라이브러리

베르나르 베르베르의 소설 ‘신’에는 인문학적 통찰뿐만 아니라 수학 지식도 담겨 있다. 미카엘 팽숑은 그의 소설에 자주 등장하는 인물인데, 이 소설에 미카엘이 사는 빌라의 주소가 ‘142857호’로 돼 있다. 다음은 신 58절에 나오는 구절이다. 출처를 에드몽 웰즈의 ‘상대적이며 절대적인 지식의 백과사전’이라고 적고 있지만, 실제로는 이 책의 저자가 베르베르 자신이다.

142857은 숫자 9와도 관련이 깊다. 이 수에 7을 곱하면 999999가 된다. 142857을 세 자리씩 나눠 더하면 142+857=999이고, 두 자리씩 나눠 더하면 14+28+57=99가 된다. 142857에 2, 3, 4, 5, 6을 곱한 수에서도 같은 특징이 나타난다.

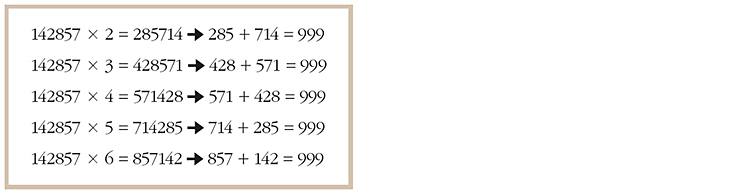
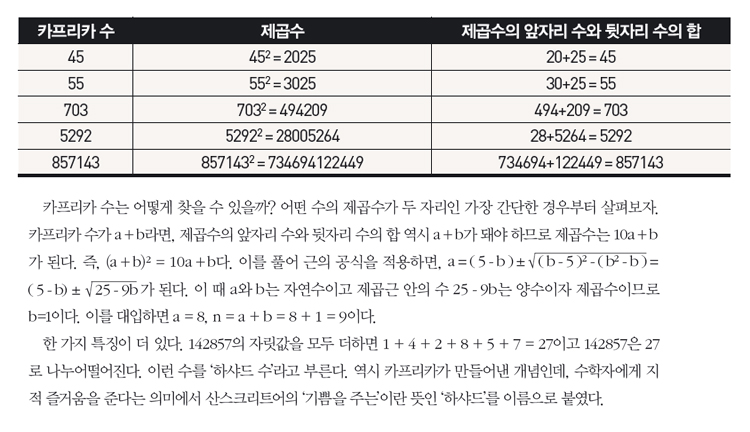
마지막으로 142857의 제곱은 20408122449이고, 앞자리 20408과 뒷자리 122449를 더하면 142857이 된다. 이처럼 제곱한 수의 앞자리 수와 뒷자리 수를 더했을 때, 원래 수와 같아지는 것을 ‘카프리카 수’라고 한다. 대표적으로 모든 자릿값이 9로만 이뤄진 수가 그렇다. 예를 들어, 9를 제곱한 81에서 8+1은 9다. 99를 제곱한 9801에서 98+1=99다. 이 외에도 45, 55, 703, 5292, 857143 등이 카프리카 수다. 인도의 수학 교사인 카프리카(1905~1986)가 만든 개념으로, 그는 공식적인 대학원 교육을 받지 못했지만 평생 수학을 가르치면서 수의 성질을 연구했다.

문학적으로 뛰어난 수학책을 배출한 나라

카프리카는 ‘카프리카 상수’도 정의했다. 모든 자릿값이 같지 않은 임의의 세 자리 혹은 네 자리 수에서 특정한 방식으로 빼는 과정을 반복할 때 수렴하는 수를 말한다. 특정한 방식이란, 주어진 수의 자릿값으로 만들 수 있는 가장 큰 수에서 가장 작은 수를 빼는 것이다. 예를 들어, 213의 자릿값을 재배열해 만들 수 있는 가장 큰 수 321에서 가장 작은 수 123을 빼면 198이 된다. 198에 같은 과정을 적용하면, 981-189=792다. 이를 계속하면, 어느 순간부터 495가 반복해서 나온다(오른쪽 표). 즉, 495에 수렴하는 것이다. 따라서 카프리카 상수는 495다. 네 자리 카프리카 상수는 6174다.

다음은 세 자리 카프리카 상수 495가 도출되는 과정을 정리한 도표다. 001부터 999까지의 수 가운데 세 자릿값이 모두 같은 111, 222, …, 999를 제외하고 나머지 990개는 모두 7단계 내에 495로 수렴한다. 아래 그림에서 1, 10, 11을 포함한 54개의 수에 이 과정을 적용하면 99가 되고, 99를 포함한 55개의 수에 대해 적용하면 891이 된다. 792, 693, 594를 거쳐 결국 카프리카 상수 495로 수렴한다.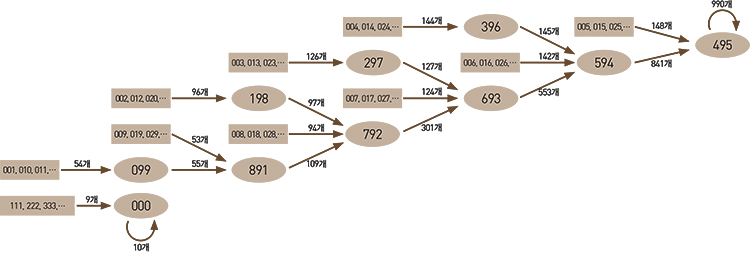


카프리카를 배출한 인도는 수학 강국으로 잘 알려져 있다. 우리나라에서는 인도인들이 19단까지 외운다고 19단 열풍이 일어나기도 했고, 간편하고 신기한 계산법인 인도의 ‘베다수학’이 유행하기도 했다. 실제로 인도는 수학의 역사를 이끄는 핵심 역할을 했다. 인도는 아라비아 숫자의 발생지이고, 0을 본격적인 숫자로 인정한 최초의 국가다. 인도의 수학자들은 다양한 방정식 해법을 연구해 대수학과 정수론 분야에 크게 기여했다.

12세기의 바스카라(1114~1185)도 그 중 한 사람이다. 바스카라는 수학자이자 ‘우자인천문대’의 책임자인 천문학자였다. 그는 저서 ‘릴라바티’를 통해 이차방정식, 삼차방정식, 부정이차방정식의 풀이법과 원주율 계산법을 소개했다. 릴라바티는 수학책이지만 신비주의적인 요소가 결합된 산스크리트 문학의 대표작으로, 문학적 가치도 높다. 당시 인도에서는 방정식을 거꾸로 계산해 푸는 ‘역산법’이 유행했다. 릴라바티에는 다음과 같이 시구의 형식으로 된 수학 문제를 역산법으로 푸는 방법이 수록돼 있다.

마지막에 얻은 값 2에서 시작해 나눈 것을 곱하고, 더한 것은 빼고, 제곱한 것은 제곱근을 구하면서 거꾸로 나가는 역산법으로 풀면, 구하고자 하는 값을 비교적 쉽게 계산할 수 있다.