d라이브러리

‘수.포.자’ 과연 그는 누구인가! 초등학교보다 중학교에 많으며, 고등학교에서는 한 반에 여러 명씩 무리 지어 다니는 그들! 심지어 네이버 국어사전에 신조어로 등재된, 우리에게 너무나 익숙한 ‘수학을 포기한 자’입니다. 때로 한반 학생의 반 이상이 수포자인 것과 달리 ‘영포자’ ‘국포자’라는 이름은 매우 생소합니다. 왜 국어, 영어 등 다른 과목들과 달리 수학은 ‘포기하게’ 되는 것일까요. 수학이 국어, 영어보다 비중이 낮거나 입시나 전공선택에서 별 의미가 없는 과목이라고 생각해서일까요? 아니면 이제 도저히 어떻게 할 수 없을 만큼 실력이 떨어져 버려서일까요?

우리를 힘들게 하는 수학! 도대체 어떻게 공부하는 것이 좋을까요. 필자가 대학시절부터 학생들을 가르치거나 공신닷컴에서 고민상담을 하면서 ‘공부법’에 관한 질문에 답을 할 때 가장 조심스럽습니다. 대부분의 학생들은 선생님이 강의를 하면 그저 ‘그렇구나’하고 수동적으로 받아들입니다. 적극적으로 왜 그런지, 다른 방법으로 할 수 있지 않은지 질문을 던지 않습니다. 이렇게 수동적인 학생들은 성공적인 선배의 공부법을 들으면 무조건 따라야만 하는 진리처럼 생각하는 경우가 많습니다. 때문에 필자를 비롯한 공신닷컴의 많은 공신들은 공부법을 얘기할 때 항상 조심스럽습니다. 마찬가지로 이번 호에 제시하는 공부방법은 ‘조언(助言)’이지 ‘법(法)’은 아니라는 점을 명심하세요. 조언을 바탕으로 자신만의 공부법을 개발해 봅시다.

그럼 먼저, 공신닷컴을 통해 접수된 수많은 수포자 또는 예비 수포자의 고민을 함께 보고 여러분의 상태를 점검해 보세요. 그리고 수동적인 자세에서 벗어나 여기 제시된 공부법을 ‘비판적’으로 접근하면서 글에서 중요한 핵심만 쏙쏙 뽑아가세요.



세 걸음 전진을 위한 한 걸음 후퇴

많은 중·고등학생들, 특히 고등학생들을 상담하면서 놀라는 점은 많은 학생들이 이전 학년에서 공부한 내용 복습보다 선행학습을 선호한다는 점입니다. 하지만 기초 없는 선행은 안 하느니만 못합니다. 선생님을 비롯한 많은 어른들이 지겨울 정도로 강조하는 부분은 복습입니다.

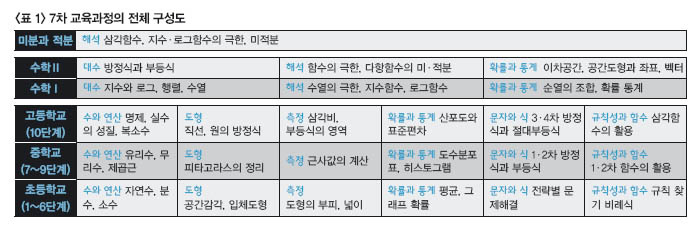
기초의 중요성은 교과과정을 보면 쉽게 이해 할 수 있습니다. <;표 1>;을 보면, 초·중·고 수학 내용과 순서가 거의 동일하게 유지되면서 점차 심화됩니다. 매우 체계적인 구성입니다. 이러한 구성을 보면 수학 공부의 방향을 알 수 있습니다. 첫째, 초등학교부터 기초를 잘 쌓으면, 중·고등학교에서 공부하는데 도움이 된다는 것입니다. 한편으로는 초등학교 때 공부가 부족했더라도 중학교 때 잘 보완하면 고등학교 공부에 크게 지장이 없다고 볼 수 있습니다. 그러니 지금 비록 성적이 안 좋더라도 수학공부를 포기할 필요는 없습니다. 물론 보완을 위한 철저한 복습은 기본입니다. 둘째, 부족한 단원이 있다면, 현재 학년수준의 개념서 뿐만 아니라 이전 학년수준의 개념서도 참조하는 것이 좋습니다.

예를 들어, 중3 학생이 피타고라스의 정리와 입체도형의 부피 등 도형의 체계를 공부하는데 중2 때까지 배운 삼각형의 존립조건, 사각형 종류별 특성이 기억나지 않는다면 1, 2 학년의 개념서부터 공부해야 한다는 말입니다. 이 얘기를 들으면 많은 학생들이 ‘본 학년 교과공부하기에도 시간이 부족한데’하고 걱정하지만 초등학교 때 성적이 바닥이었던 학생도 중학생이 된 후 초등학교 책을 보면, 훨씬 빠른 속도로 내용을 이해할 수 있습니다. 그러니 시간걱정은 붙들어 매고 시작하세요. 중요한 것은 기초와 복습입니다. 선행학습에 주력하지 마세요. 기초에는 전체 시간의 60~70%를 할애해도 아깝지 않습니다.

흔히 수학이라고 하면 문제풀이를 떠올립니다. 하지만 수학은 정의의 학문입니다. 무작정 문제를 풀기 전에 정의를 이용해 그 원리를 파악하는 것이 중요합니다. 어렵게 보이는 개념도 원리를 파악하면 간단합니다. 단기간에는 차이가 나지 않을지 몰라도 결국 웃는 사람은 원리를 정확하게 이해하는 사람입니다.
　
공식, 외우기 보다 유도과정을 기억하라

수학공부를 오래 쉬었거나 처음 시작하는 학생이 제일 먼저 시작하는 일이 바로 공식을 암기하는 것입니다. 빠르게 나가는 진도에 적응하려다 보니 생긴 문제입니다. 앞서 얘기했듯이 수학은 정의의 학문입니다. 교과서에서 개념을 설명할 때는 정의를 내린 후 개념을 설명하는 공식과 함께 유도과정이 나옵니다. 이 논리를 충실히 따르는 것을 권장합니다. 이해가 안 되는 부분은 선생님이나 친구에게 물어서 설명을 듣고 이해하는 능동적 공부를 하세요. 예를 들어보겠습니다.

집합 A={a, b, c}의 부분집합 개수는 몇 개일까요? 답은 8개입니다. 물론 n개의 원소를 가진 집합의 부분집합의 개수가 2n이라는 공식으로 구한 학생들이 많을 것입니다. 원소의 개수가 3개이니, 23=8로 부분집합의 개수는 8개. 그런데 왜 2n인가요? 바로 답할 수 있으신가요?

공식이 왜 그렇게 되는지 질문을 하는 것이 깊게 이해하는 지름길이며, 비판적 사고에 기인한 공부방법입니다. 수학을 잘 하고 싶다면, 깊이 있게 공부하세요.