d라이브러리

MIE(Magazine in Education). 넌 누구냐?

사회가 경제적으로 정치적으로 발전하면서 사회를 반영하는 교육도 변해왔다. 우리나라가 선진국과 경쟁하려면 암기와 대량생산보다 창의성과 지식의 융합이 중요하다.

암기-재생의 시대 → 표현의 시대(90년대 논술) →창의성과 융합의 시대(통합논술)

이제는 새로운 지식을 만들기 위해 서로 다른 영역이 소통하고 융합하는 시대가 열리고 있다.

‘이기적 유전자’ 이론을 사회 현상에 적용하는 과학자도 있고, 개미 연구에 심리학을 도입하는 과학자도 있다. 작년에 세상을 떠난 스티브 잡스는 휴대폰에 사람의 ‘감성’을 융합시킨 대히트작 아이폰을 탄생시켰다. 인터넷, SNS를 통해 정보가 빛의 속도로 퍼져나간다. 클릭 하나면 궁금한 것을 해결할 수 있다. 이런 정보의 바다에서 자신에게 필요하고 유용한 정보를 선택해 창의적으로 사용하는 능력이 필요하다.

통합논술이나 입학사정관제에도 이런 사회적 변화가 반영된다. 따라서 교과지식에만 머무르지 말고 과학동아 등 다양한 매체를 활용해서 공부해야 한다.

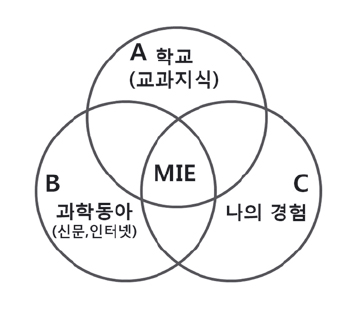
그런 점에서 과학동아(잡지)를 교육에 활용하는 MIE는 매우 좋은 공부방법이다. 통합사고력을 기르는 데 적합하기 때문이다. MIE는 ‘A. 학교’, ‘B. 과학동아’, ‘C. 나의 경험’ 이 세가지가 어우러질 때 진정한 효과를 나타난다. 학교에서 배운 교과지식은 MIE의 기초다. 기초가 탄탄해야 높은 건물이 올라가듯, 교과지식이 탄탄할수록 MIE의 효과는 커진다. 과학동아를 비롯한 신문, 인터넷 등은 MIE를 위한 다양한 자료다. B영역은 과학과 관련한 흥미로운 기사들을 다룬다. 하지만 B영역이 A영역과 만나지 않는다면, 단순히 홍미와 상식을 늘리는 백과사전 지식만 제공할 뿐이다.

과학동아에서 후쿠시마 원전사고, 쓰나미를 다룬 기사는 교과서에서 미처 다루지 못한 내용을 재미있고 자세하게 소개한다. 이런 경우 교과지식은 과학동아를 통해서 더 풍부해지고 다양해진다. 예를 들어, 융합형 과학 교과서의 ‘에너지와 환경-에너지의 순환과 기후변화’ 단원에서 간단하게 언급한 ‘해류와 대기의 대순환이 지역별 기후에 미치는 영향’을 배운 후, 과학동아 2011년 8월호 ‘슈퍼장마 부르는 제트기류’에서 기후변화의 원인인 고기압과 저기압의 형성원리를 더 자세하게 공부하는 것이다.

한발 더 나가서 나의 경험, 일상생활을 과학적 안목으로 관찰하고 해석해야 한다. 이런 과정에서 서서히 창의적이고 과학적인 추론능력이 생긴다. 이 세 영역의 만남을 마음에 새기자.





실제 고등학생이 과학동아를 MIE활동에 활용한 사례를 바탕으로 재구성한 다음의 글을 보면 이해하기 쉽다.

수진이의 MIE 입문

수진이는 고1이다. 수진이는 요즘 학교에서 ‘고1을 위한 과학논술’ 수업을 받는다. 매주 토요일 진행되는 수업을 벌써 다섯 번쯤 하고 나니 머릿속에 MIE라는 단어가 맴돌기 시작했다. 길을 갈 때도, 학원 수업을 들을 때도, TV를 봐도, 잘 때도, 마치 여름밤 모기처럼 왱왱거렸다. 논술수업시간에는 논술문제도 풀지만 신문이나 과학동아 내용을 스크랩하고 발표한다. 그런데 사실, 지난번 수업은 충격이었다. 친구 진산이의 발표였는데, 신문을 스크랩해왔다. A4용지에 전면광고 사진하나 붙여 놓고는 삐뚤빼뚤한 문장으로 이렇게 적었다.

“곧 넘어질 것이다. 멈출 수 없다. 관 성!”

이게 뭐야? 무성의하고 엉뚱하다. 그런데 선생님 반응은 더 의외다. 만약 점수를 준다면 백점 만점이라니! 광고 사진을 보고, 단 세 줄로 선생님이 원한 모든 내용을 담아 냈다고 극찬하신다. 상황요약(곧 넘어질 것이다), 과학교과 시간에 배운 개념(관성), 그리고 상황에 대한 설명(멈출수 없다)이 모두 담겨 있다. 평범한 주변 현상을 과학의 눈으로 바라보는 안목과 과학시간에 배운 지식으로 일상의 모습과 사건을 설명하고 이해하는 힘이 있었다. 선생님은 신문이나 과학동아를 보고 스크랩하면서 이런 감각을 예리하게 단련시키는 것이 바로 MIE라고 강조했다.



퍼뜩! 떠오른 생각

선생님 말씀을 전부 이해한 건 아니지만 전에는 그냥 지나치던 일상이 이제는 범상치 않게 다가온다. 일요일 오전, 수진이는 친구들과 농구시합을 했다. 격렬한 부대낌, 농구공이 골대 안으로 빨려 들어갈 때 쾌감은 한 주의 스트레스를 단숨에 날려 버린다. 그런데 갑자기 엉성한 자세로 던지는 일명 ‘막슛’의 성공률이 높은 이유가 뭔지 궁금했다. 슛을 넣는 각도와 어떤 관계이고, 어떤 과학 원리가 들어있을까. 시합을 하는 중에도 한번 떠오른 생각은 쉽게 지워지지 않았다. 수진이는 인터넷 검색창을 열었다.

과학동아와 체육교과서에서 찾은 막슛의 비밀

검색창에 ‘막슛’을 썼더니, ‘왼손은 거들 뿐, 막슛의 비밀’등의 결과가 나왔다. 검색창에 나오는 결과가 다 좋은 정보는 아니다. 수진이는 지식검색을 주로 이용하지만, 나온 내용을 100% 믿지 않는다. 검색엔진은 좀 더 믿을만한 좋은 정보를 소개하는 곳일 뿐이다. 상대적으로 오류가 적고 믿을 만한 자료는 신문이나 과학동아, 출판된 책 내용을 발췌한 글이나 전문가 블로그다. 수진이는 여러 검색 결과 목록 중에서 ‘농구 막슛 65% 성공률의 비밀’이라는 제목을 클릭했다. 과학동아 기사였다.

농구 막슛 65% 성공률의 비밀

바스켓을 향해 슛한 농구공은 물리적으로 투사체라고 할 수 있다. 농구공은 날아가는 최대거리보다 코트바닥에서 3.05m 높이에 있는 지름 45cm짜리 링에 넣어야하는 정확성이 중요한 투사체다. 따라서 슈터는 농구공의 초기 투사속력과 투사각도를 세밀하게 조절해야 한다. 물론 움직이거나 점프하면서, 또는 수비수에 대처하면서 정확한 슛을 쏘아야 하기 때문에 더욱 힘들어진다. 슈터는 수분의 1초 동안 적절한 슛의 형태를 결정해서 투사속력과 각도를 조절해야 한다.

어쨌든 슛한 공이 골인되는 것이 목표이므로 공이 바스켓으로 빨려들어가는 투사속력의 범위나 투사각의 범위가 넓으면 좋다. 미국의 천체물리학박사 피터 브란카지오는 자신의 저서 ‘스포츠과학: 물리법칙과 최적동작’에서 행한 계산에 따르면, 높은 투사각도의 슛이 직선으로 던진 슛보다 바스켓에 도달하는 속력의 범위가 넓다. 다시 말해 투사각도가 높은 경우의 슛이 낮은 경우보다 성공률이 높다는 것이다. 이것이 바로 우리가 슛을 할 때 왜 커다란 포물선으로 던지는지를 알려주는 사실이다.
그러고보니, 슈팅 각도를 크게 하면 골이 잘 들어갈 때가 많다. 각도와 슛 성공률. 수진이는 체육교과서를 꺼냈다. 선생님이 체육교과서는 과학책 같다고 그랬는데 정말 그랬다. 충격량, 자유낙하, 포물선운동, 원심력과 구심력등 과학 시간에 배운 것이 체육교과서에 나와 있다. 농구 단원에서는 다음과 같은 내용이 나왔다.

공의 입사각과 슛의 성공률


슛한 공이 그리는 궤적, 즉 포물선의 각도가 크면 클수록 슛이 성공될 확률은 높아진다. 그림에서와 같이 링 바로 위에서 보았을 때 포물선 각도가 클수록 슛 성공 가능 면적이 넓고, 각도가 작아질수록 슛 성공 가능 면적이 작아진다.
그림과 설명을 보니 60°로 들어올 때 ‘성공가능면적’이 넓고, 20°로 들어오면 그 면적이 다르다. 골대 크기는 변하지 않는데 슛 성공 가능 면적이 변한다는 것은 무엇을 의미하는 것일까. 수진이는 수학시간에 배운 정사영을 떠올렸다.

블로그에서 찾은 정사영의 정의

정사영(正射影)이란, 한자 뜻처럼 똑바로 위에서 빛을 쏴서 만든 물체의 그림자를 말합니다.

예를 들어 공중에 떠 있는 물체가 땅에 만드는 그림자를 이 물체의 정사영이라고 보면 됩니다. 공의 정사영은 항상 원입니다. 정육면체의 경우 사영을 내릴 평면체의 위치에 따라 정사각형, 직사각형, 육각형 등 여러 모양이 될 수 있습니다. 어떤 의미에서 사진을 찍는 것은 물체의 정사영을 찍는다고 할 수도 있습니다.


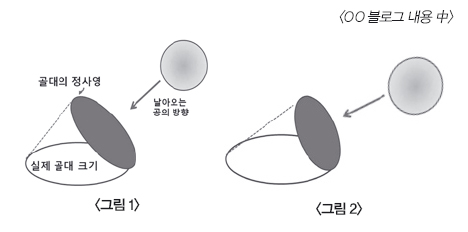
골대 크기는 변하지 않아도 공이 어떤 각도로 들어가느냐에 따라 골대의 정사영이 달라진다. 공이 바라보는 골대의 크기가 달라진다.

<;그림 1>;은 공이 높은 각도로 들어올 때, <;그림 2>;는 공이 낮은 각도로 들어올 때다. 실제 골대 크기는 변함없지만 들어오는 공이 바라보는 골대의 크기는 달라진다.

정사영의 원리를 적용하니 큰 각도로 공을 던져야 성공률이 높아지는 것이 이해된다.



정사영이 미술 속에도

정사영의 원리를 다른 곳에도 적용할 수 있을까. 도로바닥의 글씨는 길쭉하게 써야 차 안에서는 정상적인 크기로 보인다. 얼마 전 누나가 사온 책 ‘놀이와 예술, 그리고 상상력(진중권, 휴머니스트)’에서 눈여겨 본 그림이 있다. 한스 홀바인이라는 화가가 그린 ‘대사들(the ambassa-dors)’이다. 그림 아래 부분을 유심히 보면 뭔가 이상하다. 그림의 왼쪽 아래 모서리에서 대각선방향으로 비스듬히 바라보면 이것의 정체가 드러난다. 바로 ‘해골’이다.

다시 과학동아로

수진이는 학교에서 배운 정사영 개념을 이렇게 적용한 건 세계 최초인 것 같은 기분에 어깨가 으쓱했다. 스포츠를 주제로 관련된 내용을 꾸준히 정리해 보는 것도 좋은 포트폴리오가 될 것 같았다. 수진이는 동아사이언스 홈페이지(www.dongascience.com) 검색창에 ‘스포츠’를 입력하고 클릭했다.

수진이처럼 과학동아를 이용해 학교에서 배운 내용, 일상생활을 과학적으로 생각하는 일은 재미있는 작업이다. 앞으로 이 코너에서는 과학동아를 활용한 MIE활동을 안내한다. 과학동아 동아리 활동이나 자기주도적 학습, 포트폴리오 만들기, 논술 준비에 이용해 보자.