d라이브러리

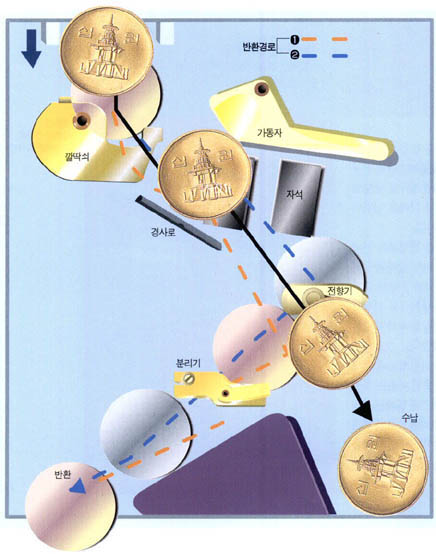
얼마 전까지 우리나라와 미국의 자유무역협정(FTA) 때문에 나라 전체가 시끌벅적했다. 이 일에 대해 한 정당의 대표는 “한미 FTA라는 배는 이제 전혀 다른 바다 위를 떠가고 있는데, 이 마당에 한미 FTA가 무조건 국익이라고 각주구검(刻舟求劍)하는 것은 옳지 않다”고 주장했다. 여기서 각주구검을 한자로 풀면 ‘새길 각(刻)’ ‘배 주(舟)’ ‘구할 구(求)’ ‘칼 검(劍)’으로 ‘배에다 새겨 놓고 검을 찾는다’는 뜻이다.

좌표표시를 한 것까지는 좋았는데
칼을 강물에 떨어뜨리자 뱃전에 표시를 했다가 나중에 그 칼을 찾으려 한다는 사자성어인 각주구검은 어리석은 일이나 완고한 사람을 풍자하는 말이다. 이 우화는 진나라의 재상 여불위(呂不韋, ?~기원전 235년)가 그의 식객들에게 편집시킨 ‘여씨춘추’(呂氏春秋)라는 책에 나와 있다. 이 책은 고금을 통한 천지만물의 일들을 30여만 어구(語句)로 엮은 대사서(大辭書)다.

중국 전국시대 초나라의 한 젊은이가 귀한 검 한 자루를 지닌 채 배를 타고 양쯔강을 건너고 있었다. 그런데 배가 강 한복판에 이르렀을 때 그만 실수로 손에 들고 있던 검을 강물에 떨어뜨리고 말았다.
“이런, 이를 어쩐다 ….”
젊은이는 얼른 허리춤에 차고 있던 단검을 꺼내더니 검을 떨어뜨린 그 뱃전에다 표시를 하면서 중얼거렸다.
“ 검이 떨어진 곳이 여기니까 배가 닿으면 찾아봐야지!”

이윽고 배가 나루터에 닿자 그는 곧 옷을 벗어 던지고 표시를 한 뱃전 밑 강물 속으로 뛰어들었다. 젊은이는 배 밑을 샅샅이 뒤졌지만 검이 그 밑에 있을 리가 없었다.

각주구검은 너무 엉뚱한 비유라서 세상에 이런 사람이 있을 것 같지 않지만, 실제로는 어리석음에 덮여서 이런 행동을 하는 사람들이 많다. 각주구검과 비슷한 의미를 가진 고사성어로 수주대토(守株待兎)라는 말이 있다. 수주대토를 그대로 해석하면 ‘그루터기를 지키며 토끼를 기다린다’는 뜻으로 완고함과 미련함을 비유한 말이다. 이 고사는 ‘한비자’(韓非子)에 다음과 같은 내용으로 소개돼 있다.

어느 날 송나라의 한 농부가 길을 가다가 그루터기에 부딪혀 죽은 토끼를 주웠다. 그런 일이 있은 뒤 농부는 모든 일을 제쳐두고 날마다 그 그루터기에 앉아 토끼가 나타나기만을 기다렸다. 그러나 토끼가 다시 나타나 같은 곳에 부딪혀 죽을 리는 없었기 때문에 사람들은 모두 그를 비웃었다.

각주구검이라는 고사에서 검을 떨어뜨린 젊은이는 어리석게도 강에 떠 움직이는 배에 위치를 표시했고, 수주대토라는 고사에서 농부는 그루터기를 지키며 토끼가 지나가기를 미련하게 기다렸다. 그러나 수학의 관점에서 생각해보면 한 사람은 좌표평면에 한 점의 위치를 표시했으며, 다른 한 사람은 어떤 일이 일어난 위치를 정확히 알고 있었던 위치표시의 선구자라고 볼 수 있지 않을까.

기하학, 대수학을 만나다
어떤 위치에 표시를 하는 일이 수학에서는 어떤 의미가 있을까? 수학에서 위치를 표시했다는 것은 좌표평면을 사용했다는 말이고, 이는 곧 해석기하학을 이용했다는 뜻이다. 17세기 초반 수학에서 가장 큰 업적은 해석기하학의 발전이다. 해석기하학이란 기하학적인 대상을 그에 대응하는 대수적인 고찰로 바꿔 탐구하는 분야다.

해석기하학이 이러한 능력을 갖게 된 것은 대수적 처리 과정과 기호가 발전되고 난 이후이며, 이 분야에 프랑스의 수학자 데카르트와 페르마가 활력을 불어 넣은 뒤에야 비로소 우리에게 익숙한 형태의 해석기하학이 탄생했다.

예를 들면, 기하학에서 타원, 포물선, 쌍곡선을 ‘원뿔곡선’이라고 한다. 원뿔곡선은 아래 그림과 같이 두 개의 원뿔을 맞붙였을 때 자르는 방법에 따라 나타날 수 있는 기하학적인 모양이다. 고대 수학자들은 이와 같은 곡선들을 작도하는 방법과 그에 따른 여러 가지 성질을 밝혀냈지만 이런 곡선들을 오늘날과 같은 대수적인 식으로 표현하지는 못했다.
그러다가 데카르트가 좌표평면을 도입하고, 대수적인 기호들을 본격적으로 사용하게 된 뒤에는 타원, 포물선, 쌍곡선을 각각 다음과 같이 표현할 수 있게 됐다.

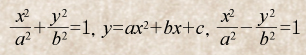
그리하여 비로소 기하학적인 도구가 아닌 대수적인 도구로 이들을 연구할 수 있게 됐다.
데카르트는 공간에 좌표를 설정하면 기하학에서 다루는 도형을 수 사이의 관계인 함수로 나타낼 수 있다고 생각했다. 또한 반대로 함수도 기하학적인 도형으로 표현할 수 있다고 생각했다. 함수와 도형을 연결시킨 그의 착상은 도형 그 자체를 연구할 때도 중요한 수단이 됐을 뿐 아니라 함수를 도형으로 나타낼 수 있게 됨으로써 직관적으로 고찰할 수 있게 됐다. 함수의 그래프를 처음으로 좌표평면에 나타낸 그를 해석기하학의 창시자라고 부르는 이유다.

데카르트가 좌표평면을 도입한 뒤 해석기하학은 함수를 본격적으로 다루는 학문으로 발전했다. 운동하거나 변화하는 구체적인 현상을 표현하는 곡선의 방정식도 좌표평면 상의 함수로 여겼다. 이 후 라이프니츠, 오일러, 코시, 디리클레 같은 수학자들은 곡선과 함수의 개념을 더욱 발전시켰다.

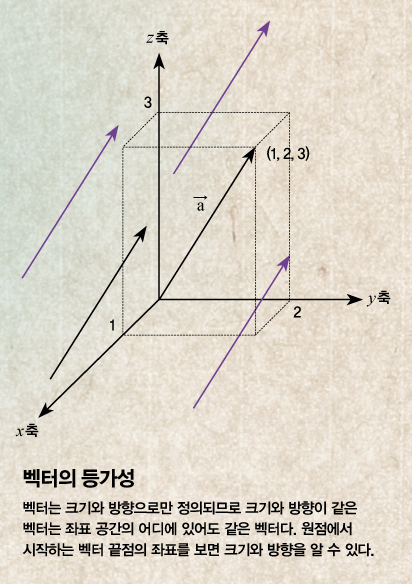
좌표평면의 도입은 물리학에서 주로 사용되고 있는 벡터를 간단히 다룰 수 있게 했기 때문에 물리학 발전에도 큰 영향을 미쳤다. 길이, 넓이, 질량, 온도 같이 그 양의 크기만 주어지면 완전히 표시되는 스칼라와 달리 벡터는 힘, 속도같이 크기뿐 아니라 방향까지 지정해 어떤 수학적 현상을 나타내는 방식이다. 2차원, 3차원 공간의 벡터는 보통 방향이 있는 선분 즉, 화살표를 써서 표현하는데, 화살표는 벡터의 방향이고 그 길이는 크기를 나타낸다.

벡터는 크기와 방향에 의해서만 정의되므로 크기와 방향이 같은 벡터는 모두 같은 벡터다. 특히 좌표평면에서 원점을 시작점으로 갖는 모든 벡터는 끝점에 의해 크기와 방향이 결정된다. 그래서 실수의 순서쌍 (a, b, c)를 ‘공간벡터’라고 한다. 이를테면 벡터 a=(1, 2, 3)를 좌표평면 위에 나타내면 왼쪽 위의 그림과 같고, 그 밖에 벡터는 모두 a와 방향과 크기가 같기 때문에 a와 같은 벡터다. 즉 이 벡터들을 평행이동해 시작점을 원점에 맞추면 모두 a와 완전히 포개진다.

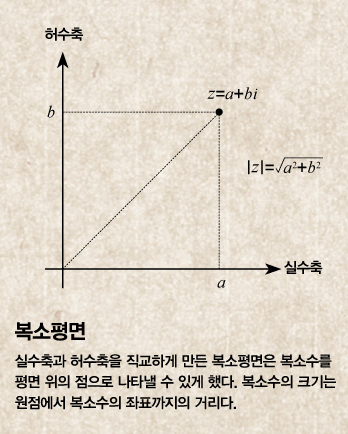
좌표평면의 도입이 수학발전에 기여한 또 다른 예는 바로 복소수 z=a+bi(a, b는 실수)의 표현이다. 즉 실수축 2개를 직교하도록 해 도입됐던 좌표평면(2차원)의 축 하나를 허수로 바꿔 실수축과 허수축이라는 두 축을 직교하도록 해 수의 세계를 실수에서 복소수로 넓혔다.

아무튼 수학을 한 단계 업그레이드시킨 좌표평면에 관한 내용이 동양에서는 이미 생활 속의 지혜로 사용됐다는 점이 흥미롭다. 물론 그 효용성을 수학이론으로 발전시키지는 못했지만.


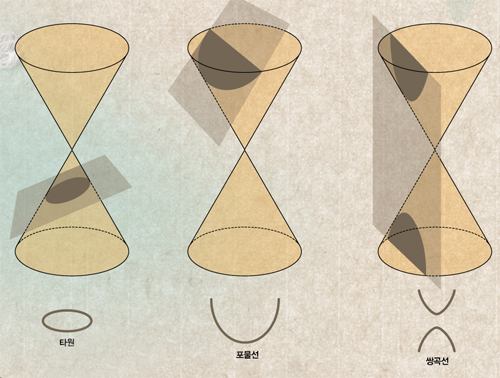
여러 가지 원뿔곡선
맞붙어 있는 원뿔을 자르는 방법에 따라 3가지 곡선이 나온다. 평면이 원뿔 하나를 관통해 접선이 닫힌곡선일 때 그 궤적은 타원(왼쪽)이다(평면이 원뿔 축과 수직일 때가 원). 평면이 원뿔 하나만을 자를 때 접선의 궤적은 포물선이고(가운데), 원뿔 양쪽을 다 자를 때 접선의 궤적은 쌍곡선이다(오른쪽).



이광연 교수는 성균관대 수학과를 졸업하고 동대학원에서 석사와 박사학위를 받았다. 그뒤 미국 와이오밍주립대에서 박사후연구원을, 아이오와대에서 방문교수를 지냈다. 현재 한서대 수학과 교수로 재직 중이며, ‘웃기는 수학이지 뭐야’ ‘신화 속 수학이야기’ ‘수학 블로그’ 같은 책을 펴냈다.