구독상품안내
제시문
다음을 읽고 물음에 답하라
(가) 유체가 유선을 그리며 흐를 때 역학적 에너지는 보존된다. 이를 바탕으로 두 점 A와 B의 높이, 두 점에서의 압력과 흐르는 속도 사이의 관계를 수식으로 나타내면 다음과 같다. 이를 베르누이 방정식이라 한다.
P+ρgh+1/2ρv2=일정
한 점에서 위치에너지와 운동에너지, 압력 P로 인한 일(에너지)을 합한 값은 다른 점에서 세 에너지를 합한 값과 같다. 유체의 밀도는 변하지 않는다고 가정하고 밀도 ρ를 써서 위치에너지와 운동에너지를 나타낸다. 이때 압력은 유체가 움직이지 않을 때 압력과 같지 않다. 관계식처럼 흐르는 유체의 압력이 유속, 기준점에 대한 높이와 관련 있으므로 이를 이용해 유체의 속력을 구한다. 송유관을 흐르는 기름의 속도, 비행기의 속도를 측정할 때 베르누이 방정식을 이용해 구한다.
(나) 유관 내에 유체가 흐를 때 유관의 모든 단면에서 질량유량은 동일하다. 비압축성 유체의 경우 체적유량은 통과하는 관로 면적에 관계없이 일정하다. 통과하는 단면의 면적이 작아지면 유속이 빨라져 일정 유량을 유지한다. 물이 호스를 통해 들어오고 나갈 때 들어오는 곳의 면적이 A1, 속도가 v1이고 나가는 곳의 면적이 A2, 속도가 v2면 A1Xv1= A2Xv2이며 이를 연속방정식이라 한다.
(다) 1653년 블라제 파스칼은 ‘밀폐된 용기에 담긴 유체에 가해진 압력이 유체의 모든 부분과 유체를 담은 용기의 벽까지 세기가 감소되지 않고 전달된다’는 원리를 발견했다. 압력이 변할 때 부피가 바뀐다는 점만 고려하면 파스칼의 원리는 기체에도 적용된다. 힘 F와 면적 A에 작용하는 압력 P 사이에는 F=PXA와 같은 관계식이 성립한다.
(라) 점성이 없는 이상유체는 운동 중에도 접선변형력이 항상 0이다. 흐르는 방향으로 힘이 작용하지 않으므로 어떤 물체도 흐름에 밀려 떠내려가지 않는다. 이는 점성을 무시해 실제와 다르게 나타나는 현상이다. 생각의 편의를 위해 가상적으로 만든 유체를 완전유체라고 하며 완전유체역학은 유체에 점성과 압축성이 없다고 가정한다. 이렇게 가정하면 기초방정식을 해석하기 쉬워 물체 주위의 흐름을 간단히 파악할 수 있다. 이 방법으로 비행기 날개가 받는 양력을 계산하면 실험결과와 잘 맞는다. 그러나 물체 표면 가까이(경계층)나 충격파 내부처럼 점성을 무시할 수 없는 경우에는 적용하지 못한다.
베르누이 방정식과 연속방정식을 이용해 유체의 운동을 파악해 봅시다.
문제 1
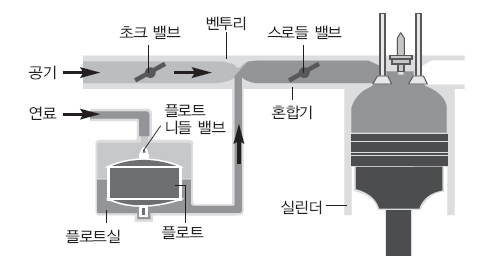
다음 그림은 자동차 부품인 기화기를 간단히 나타낸 것이다. 제시문 (가)와 (나)를 참조해 기화기 안에서 연료와 공기가 혼합되는 원리를 설명하라.
전문가 클리닉
연속방정식과 베르누이 정리를 실제 현상에 적용시킵니다. 단면적이 좁아질 때 유체 압력의 변화를 추측하고 압력의 변화가 연료와 공기가 섞이는 데 어떤 영향을 줄지 생각해 봅니다.
예시답안
벤투리 부분에서 공기가 흐르는 단면적이 갑자기 줄어든다. 단면적이 작아지면 연속방정식에 의해 공기가 빠른 속도로 벤투리 부분을 지난다. 베르누이 정리에 따르면 유체 속도가 빨라질 때 그 부분의 유체 압력이 작아진다. 따라서 공기 압력이 낮아지고 압력만큼 연료탱크에서 연료를 빨아들인다. 빨아들이는 힘이 충분히 크면 연료가 벤투리 부분에서 분사돼 공기와 섞인다.
배경지식
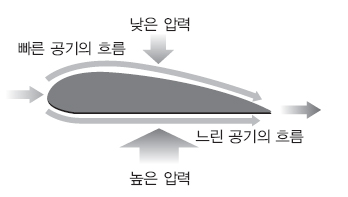
유체 흐름에 대한 베르누이의 정리를 이용한 대표적인 예는 비행기 날개다. 공중에서 비행기 중량을 지탱하는 힘은 날개(주날개)에 작용하는 양력이다. 비행기가 공기 속을 전진하면 같은 속도의 바람(공기의 흐름)이 날개에 닿는다. 공기흐름이 만곡이 큰 날개 윗면을 통과하면 유속이 빨라지고 만곡이 작은 아랫면에서는 유속이 느려진다. 베르누이의 정리에 따르면 유속이 증가할 때 유체 압력이 감소하고 유속이 감소하면 압력이 증가한다. 날개 윗면에는 부압(negative pressure)이 생기고 아랫면에는 정압(positive pressure)이 생겨 날개를 위로 밀어 올린다. 두 힘이 합쳐져 날개에 상향하는 양력이 생긴다. 비행기가 일정한 속도로 수평비행하면 날개 양력이 기체 중량과 균형을 잡는다.
문제 2
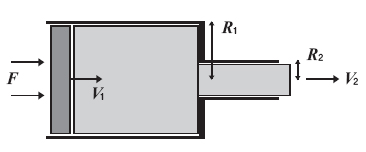
안쪽반지름이 각각 R1, R2인 파이프가 같은 중심축으로 연결돼 있다. 물이 채워진 상태에서 왼쪽 파이프의 피스톤에 힘 F를 가했을 때 피스톤이 움직이는 속도 V1과 오른쪽 파이프를 통과해 분사되는 물의 속도 V2를 구하라. 단 물의 밀도는 ρ이고 완전유체로 가정해 물의 점성과 표면장력을 무시한다.
전문가 클리닉
연속방정식과 베르누이의 정리는 유체 운동을 결정합니다. 피스톤이 움직이는 부분과 물이 분사되는 부분에서 위치에너지, 운동에너지, 압력에 의한 에너지를 구하고 연속방정식과 베르누이의 정리를 이용해 물의 속도를 구합니다.
예시답안
배경지식
일본 차세대 쾌속선 ‘테크노 슈퍼 라이너’는 종래 선박에 비해 2배나 빠른 속도인 시속 90km로 항해할 수 있어 바다의 신칸센이라 불린다. 테크노 슈퍼 라이너는 실험을 끝내고 기술적으로 실용화 단계에 접어들었다.
테크노 슈퍼 라이너의 큰 특징은 배 자체가 지니는 부력과 더불어 부상을 돕는 기관이나 부상팬이 장착돼 있다는 점이다. 대부분 배가 항행할 때 파도의 저항이나 물과의 마찰 때문에 추진 성능이 떨어지게 된다. 그러나 테크노 슈퍼 라이너는 부상한 상태에서 항행하므로 해수와 접촉하는 면적이 작아 저항이 작고 파도의 영향을 받지 않으며 추진할 수 있다.
추진 장치도 통상 배와 다르다. 통상 배는 스크루 프로펠러로 물을 뒤로 보내 추진력을 얻는데 테크노 슈퍼 라이너는 워터제트를 사용한다. 워터제트 추진기관은 배 밑에서 빨아올린 물을 뒤쪽으로 분출해 반작용으로 추진력을 얻는 장치다. 워터제트를 사용하면 고속에서도 안정적인 항행이 가능하다.
문제 3
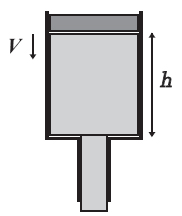
파이프에서 피스톤을 빼낸 뒤 물을 채우고 그림과 같이 수직으로 세웠다. 그러자 두 파이프의 경계면을 기준으로 높이 h만큼 물이 채워졌다. 이때 수면이 내려가는 속도 v를 h에 대한 함수로 나타내라.
전문가 클리닉
문제 2)의 상황에서 어떤 부분이 바뀌었는지 생각해 봅니다. 피스톤으로 가해지던 힘이 채워진 물의 무게로 바뀌었습니다. 이 점을 고려하고 연속방정식과 베르누이의 정리를 이용해 수면이 내려가는 속도를 구합니다.
예시답안
문제 4
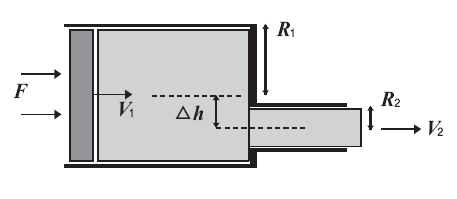
그림과 같이 오른쪽 파이프가 왼쪽 파이프의 중심선보다 △h만큼 내려가 있을 때 물이 분사되는 속도 V2는 커지는지 작아지는지를 간략히 설명하라.
전문가 클리닉
위치에너지는 베르누이의 정리에 포함됩니다. 문제 2)의 상황에서 위치에너지 항이 바뀐 경우입니다. 이를 고려해 문제를 해결합니다.
예시답안
배경지식
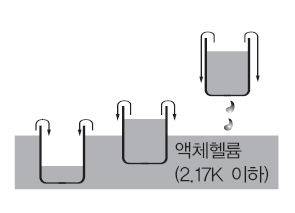초유동(superfluidity)이란 액체가 점성 없이 흐르는 현상이다. 이와 같은 현상은 액체헬륨에서 2.17K 이하인 저온일 때만 발견되며 다른 액체에서는 발견되지 않는다. 초유동을 보이는 액체를 초유체라 고 하며 액체헬륨 가운데 천연으로 존재하는 질량수 4인 He가 2.17K 이하에서 초유동을 나타낸다. 동위원소로 질량수 3인 He는 이 온도에서 초유동을 보이지 않는다. 그러나 0.0027K(2.7mK) 이하에서는 초유동을 나타낸다. 오른쪽 그림과 같이 2.17K 이하인 액체헬륨 속에 물통을 넣으면 액체헬륨이 얇은 막을 이뤄 물통 벽을 따라 상승해 물통 속으로 들어간다. 물통을 액체 표면에서 들어올리면 다시 벽면을 따라 물통 밖으로 되돌아간다. 이 현상은 물과 같은 보통 유체에서는 결코 일어나지 않는다.
다음을 읽고 물음에 답하라
(가) 유체가 유선을 그리며 흐를 때 역학적 에너지는 보존된다. 이를 바탕으로 두 점 A와 B의 높이, 두 점에서의 압력과 흐르는 속도 사이의 관계를 수식으로 나타내면 다음과 같다. 이를 베르누이 방정식이라 한다.
P+ρgh+1/2ρv2=일정
한 점에서 위치에너지와 운동에너지, 압력 P로 인한 일(에너지)을 합한 값은 다른 점에서 세 에너지를 합한 값과 같다. 유체의 밀도는 변하지 않는다고 가정하고 밀도 ρ를 써서 위치에너지와 운동에너지를 나타낸다. 이때 압력은 유체가 움직이지 않을 때 압력과 같지 않다. 관계식처럼 흐르는 유체의 압력이 유속, 기준점에 대한 높이와 관련 있으므로 이를 이용해 유체의 속력을 구한다. 송유관을 흐르는 기름의 속도, 비행기의 속도를 측정할 때 베르누이 방정식을 이용해 구한다.
(나) 유관 내에 유체가 흐를 때 유관의 모든 단면에서 질량유량은 동일하다. 비압축성 유체의 경우 체적유량은 통과하는 관로 면적에 관계없이 일정하다. 통과하는 단면의 면적이 작아지면 유속이 빨라져 일정 유량을 유지한다. 물이 호스를 통해 들어오고 나갈 때 들어오는 곳의 면적이 A1, 속도가 v1이고 나가는 곳의 면적이 A2, 속도가 v2면 A1Xv1= A2Xv2이며 이를 연속방정식이라 한다.
(다) 1653년 블라제 파스칼은 ‘밀폐된 용기에 담긴 유체에 가해진 압력이 유체의 모든 부분과 유체를 담은 용기의 벽까지 세기가 감소되지 않고 전달된다’는 원리를 발견했다. 압력이 변할 때 부피가 바뀐다는 점만 고려하면 파스칼의 원리는 기체에도 적용된다. 힘 F와 면적 A에 작용하는 압력 P 사이에는 F=PXA와 같은 관계식이 성립한다.
(라) 점성이 없는 이상유체는 운동 중에도 접선변형력이 항상 0이다. 흐르는 방향으로 힘이 작용하지 않으므로 어떤 물체도 흐름에 밀려 떠내려가지 않는다. 이는 점성을 무시해 실제와 다르게 나타나는 현상이다. 생각의 편의를 위해 가상적으로 만든 유체를 완전유체라고 하며 완전유체역학은 유체에 점성과 압축성이 없다고 가정한다. 이렇게 가정하면 기초방정식을 해석하기 쉬워 물체 주위의 흐름을 간단히 파악할 수 있다. 이 방법으로 비행기 날개가 받는 양력을 계산하면 실험결과와 잘 맞는다. 그러나 물체 표면 가까이(경계층)나 충격파 내부처럼 점성을 무시할 수 없는 경우에는 적용하지 못한다.
베르누이 방정식과 연속방정식을 이용해 유체의 운동을 파악해 봅시다.
문제 1
다음 그림은 자동차 부품인 기화기를 간단히 나타낸 것이다. 제시문 (가)와 (나)를 참조해 기화기 안에서 연료와 공기가 혼합되는 원리를 설명하라.
전문가 클리닉
연속방정식과 베르누이 정리를 실제 현상에 적용시킵니다. 단면적이 좁아질 때 유체 압력의 변화를 추측하고 압력의 변화가 연료와 공기가 섞이는 데 어떤 영향을 줄지 생각해 봅니다.
예시답안
벤투리 부분에서 공기가 흐르는 단면적이 갑자기 줄어든다. 단면적이 작아지면 연속방정식에 의해 공기가 빠른 속도로 벤투리 부분을 지난다. 베르누이 정리에 따르면 유체 속도가 빨라질 때 그 부분의 유체 압력이 작아진다. 따라서 공기 압력이 낮아지고 압력만큼 연료탱크에서 연료를 빨아들인다. 빨아들이는 힘이 충분히 크면 연료가 벤투리 부분에서 분사돼 공기와 섞인다.
배경지식
유체 흐름에 대한 베르누이의 정리를 이용한 대표적인 예는 비행기 날개다. 공중에서 비행기 중량을 지탱하는 힘은 날개(주날개)에 작용하는 양력이다. 비행기가 공기 속을 전진하면 같은 속도의 바람(공기의 흐름)이 날개에 닿는다. 공기흐름이 만곡이 큰 날개 윗면을 통과하면 유속이 빨라지고 만곡이 작은 아랫면에서는 유속이 느려진다. 베르누이의 정리에 따르면 유속이 증가할 때 유체 압력이 감소하고 유속이 감소하면 압력이 증가한다. 날개 윗면에는 부압(negative pressure)이 생기고 아랫면에는 정압(positive pressure)이 생겨 날개를 위로 밀어 올린다. 두 힘이 합쳐져 날개에 상향하는 양력이 생긴다. 비행기가 일정한 속도로 수평비행하면 날개 양력이 기체 중량과 균형을 잡는다.
문제 2
안쪽반지름이 각각 R1, R2인 파이프가 같은 중심축으로 연결돼 있다. 물이 채워진 상태에서 왼쪽 파이프의 피스톤에 힘 F를 가했을 때 피스톤이 움직이는 속도 V1과 오른쪽 파이프를 통과해 분사되는 물의 속도 V2를 구하라. 단 물의 밀도는 ρ이고 완전유체로 가정해 물의 점성과 표면장력을 무시한다.
전문가 클리닉
연속방정식과 베르누이의 정리는 유체 운동을 결정합니다. 피스톤이 움직이는 부분과 물이 분사되는 부분에서 위치에너지, 운동에너지, 압력에 의한 에너지를 구하고 연속방정식과 베르누이의 정리를 이용해 물의 속도를 구합니다.
예시답안
배경지식
일본 차세대 쾌속선 ‘테크노 슈퍼 라이너’는 종래 선박에 비해 2배나 빠른 속도인 시속 90km로 항해할 수 있어 바다의 신칸센이라 불린다. 테크노 슈퍼 라이너는 실험을 끝내고 기술적으로 실용화 단계에 접어들었다.
테크노 슈퍼 라이너의 큰 특징은 배 자체가 지니는 부력과 더불어 부상을 돕는 기관이나 부상팬이 장착돼 있다는 점이다. 대부분 배가 항행할 때 파도의 저항이나 물과의 마찰 때문에 추진 성능이 떨어지게 된다. 그러나 테크노 슈퍼 라이너는 부상한 상태에서 항행하므로 해수와 접촉하는 면적이 작아 저항이 작고 파도의 영향을 받지 않으며 추진할 수 있다.
추진 장치도 통상 배와 다르다. 통상 배는 스크루 프로펠러로 물을 뒤로 보내 추진력을 얻는데 테크노 슈퍼 라이너는 워터제트를 사용한다. 워터제트 추진기관은 배 밑에서 빨아올린 물을 뒤쪽으로 분출해 반작용으로 추진력을 얻는 장치다. 워터제트를 사용하면 고속에서도 안정적인 항행이 가능하다.
문제 3
파이프에서 피스톤을 빼낸 뒤 물을 채우고 그림과 같이 수직으로 세웠다. 그러자 두 파이프의 경계면을 기준으로 높이 h만큼 물이 채워졌다. 이때 수면이 내려가는 속도 v를 h에 대한 함수로 나타내라.
전문가 클리닉
문제 2)의 상황에서 어떤 부분이 바뀌었는지 생각해 봅니다. 피스톤으로 가해지던 힘이 채워진 물의 무게로 바뀌었습니다. 이 점을 고려하고 연속방정식과 베르누이의 정리를 이용해 수면이 내려가는 속도를 구합니다.
예시답안
문제 4
그림과 같이 오른쪽 파이프가 왼쪽 파이프의 중심선보다 △h만큼 내려가 있을 때 물이 분사되는 속도 V2는 커지는지 작아지는지를 간략히 설명하라.
전문가 클리닉
위치에너지는 베르누이의 정리에 포함됩니다. 문제 2)의 상황에서 위치에너지 항이 바뀐 경우입니다. 이를 고려해 문제를 해결합니다.
예시답안
배경지식
초유동(superfluidity)이란 액체가 점성 없이 흐르는 현상이다. 이와 같은 현상은 액체헬륨에서 2.17K 이하인 저온일 때만 발견되며 다른 액체에서는 발견되지 않는다. 초유동을 보이는 액체를 초유체라 고 하며 액체헬륨 가운데 천연으로 존재하는 질량수 4인 He가 2.17K 이하에서 초유동을 나타낸다. 동위원소로 질량수 3인 He는 이 온도에서 초유동을 보이지 않는다. 그러나 0.0027K(2.7mK) 이하에서는 초유동을 나타낸다. 오른쪽 그림과 같이 2.17K 이하인 액체헬륨 속에 물통을 넣으면 액체헬륨이 얇은 막을 이뤄 물통 벽을 따라 상승해 물통 속으로 들어간다. 물통을 액체 표면에서 들어올리면 다시 벽면을 따라 물통 밖으로 되돌아간다. 이 현상은 물과 같은 보통 유체에서는 결코 일어나지 않는다.
