d라이브러리

비오는 날 빗방울이 기와를 타고 흘러내리는 모습을 유심히 바라본 적이 있다. 마치 기와의 곡면 위에 구슬을 떨어뜨려도 가운데로 모여 굴러갈 것 같다. 실제로 기와의 곡선은 수학에서 다루는 사이클로이드(cycloid)와 닮았다.
 

킥보드나 자전거 바퀴 위에 붙은 발광 다이오드를 생각해보자. 바퀴가 앞으로 굴러가면 발광 다이오드를 붙인 지점도 움직이며 곡선을 그리는데, 이것이 사이클로이드다. 수학에서 사이클로이드는 원이 회전할 때 원 위의 한 점이 그리는 곡선을 뜻한다. 이 곡선은 일정한 주기로 반복된다.

사이클로이드는 수많은 과학자들의 관심을 사로잡을 정도로 매력적이었다. 사이클로이드라는 이름은 1599년경 갈릴레이가 붙였다. 1634년 프랑스의 수학자 드 로베르발은 원의 넓이와 사이클로이드 넓이의 관계를 밝혔다. 원이 한번 회전했을 때 얻어진 사이클로이드의 넓이는 정확히 원 넓이의 3배였다. 또 원이 한번 회전했을 때 생긴 사이클로이드의 길이가 또 원의 반지름의 8배라는 사실도 곧 드러났다.

호빵을 닮은 이 곡선을 뒤집어 그 위에 구슬을 놓아 보자. 구슬은 바닥으로 굴러갈 것이다. 놀랍게도 사이클로이드는 가장 짧은 시간에 구슬이 굴러가는 최단하강곡선이다. 보통 직선의 길이가 가장 짧으니까 직선 경로에서 공이 가장 빨리 굴러갈 거라 생각하기 쉽다. 그러나 사이클로이드에 구슬을 올려두면 직선보다 더 빨리 굴러간다. 사이클로이드의 이런 성질을 활용하면 어떨까. 놀이터의 미끄럼틀을 직선이 아닌 사이클로이드로 만들면 더 스릴이 넘칠지도 모른다.
 

또 여러 개의 구슬을 바닥이 아닌 다양한 위치에 놓을 경우 구슬이 동시에 바닥에 모이기 때문에 등시곡선이기도 하다. 사이클로이드 위에 공을 놓으면 도착점과의 거리에 관계없이 동시에 바닥으로 떨어진다는 얘기다. 네덜란드의 물리학자 호이겐스는 1673년 ‘진자시계’라는 책에서 진자가 사이클로이드를 따라 움직일 때 만드는 궤도가 등시곡선임을 증명하고 이 특징을 이용해 진자시계를 만들었다.

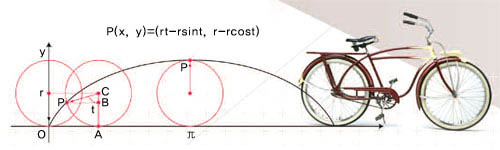
이처럼 다양한 성질을 갖는 사이클로이드는 오랜 시간동안 수학자들 사이에서 논쟁거리였다. 그래서 이 곡선은 ‘기하학자들의 헬렌(트로이전쟁의 원인이 된 미녀)’이라는 별명을 갖게 됐다. 이제 사이클로이드를 수학적으로 표현해볼까. 원이 직선 위를 회전하며 굴러갈 때 원 위의 점이 그리는 곡선을 생각해 보자.
 

원의 반지름의 길이를 r, 각 PCB의 크기를 t라 할 때 호 PA와 선분 OA는 길이가 모두 rt다. 선분 CA의 길이가 r이므로 삼각함수를 이용하면 점 P(x, y)의 좌표를 x=rt-rsint, y=r-rcost로 표현할 수 있다(그림).