d라이브러리

언뜻 보기에 암호처럼 보이는 그림들. 이 안에 어떤 비밀이 숨어있을까.

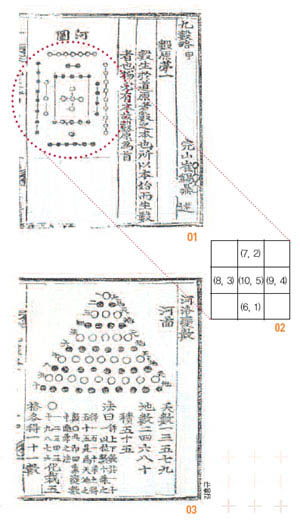
조선 후기 사대부 출신 학자인 최석정이 쓴 수학책 ‘구수략’(九數略)에는 ‘하도’(河圖)(01)에 대한 내용이 담겨 있다. 하도는 중국 복희씨 때 황하에서 용마가 입에 물고 나왔다는 전설 속의 예언서다. 하도에는 흰 점과 검은 점이 표시돼 있는데 흰 점의 개수는 홀수, 검은 점의 개수는 짝수다.

흰 점과 검은 점을 짝지어 점의 개수를 정사각형 안에 숫자로 나타내보자(02). 어느 것이나 차가 5임을 알 수 있다. 최석정은 하도에 등장하는 점의 개수와 수를 같이 기록해 홀수를 천수(天數), 짝수를 지수(地數)로 표현했다. 천수는 1, 3, 5, 7, 9로 그 합이 25고, 지수는 2, 4, 6, 8, 10으로 그 합이 30이다.

하도에 대한 최석정의 해설을 현대적으로 풀이하면 다음과 같다.

“1+10=11, 2+9=11, 3+8=11, 4+7=11, 5+6=11이므로 1부터 10까지의 합은 55다.”

“삼각형 모양으로 배열된 그림(03)을 뒤집어 원래 삼각형 옆에 붙이고 점의 개수를 세면 각 줄에 있는 점의 개수는 모두 11개다. 모든 점은 110개고 이 값의 반이 바로 55가 된다.”

1부터 10까지의 합을 구하는 방법이 조금 익숙하지 않은가. 바로 고등학교 수학Ⅰ 교과서에 실린 독일 수학자 가우스의 에피소드가 떠오른다. 가우스가 이 계산법으로 10살 때 사람을 놀라게 했다지만 최석정이 죽은 해가 1715년이고 가우스가 태어난 해가 1777년이므로 시기적으로 최석정이 앞섰음을 알 수 있다.

하도에 나타나는 1부터 10까지의 자연수를 작은 수부터 차례로 나열하면 이웃항의 차가 모두 1이 된다. 이러한 수의 배열을 등차수열이라고 한다. 최석정이 구한 1부터 10까지의 합은 등차수열의 합과 같다.

우리 생활 속에서 등차수열의 예를 찾아보자. 2007년 1월의 달력에는 모두 다섯 주가 있는데, 가로줄의 날짜는 차가 1인 등차수열이고 세로줄의 날짜는 차가 7인 등차수열이다.

2008년 중국 베이징에서 올림픽이 열린다. 그렇다면 그 다음 올림픽은 언제 개최할까. 바로 4년 뒤인 2012년이다. 올림픽이나 월드컵 같은 행사는 4년을 주기로 열리므로 이웃항의 차가 4인 등차수열을 이룬다.

교통 혼잡을 줄이고 에너지를 절약하기 위해 10부제에 참여하는 사람들이 늘고 있다. 10부제는 차량번호와 날짜의 끝자리수가 일치하는 날을 기준으로 열흘에 한 번씩 차를 몰지 않는 제도다. 차량번호가 5316이라면 1월에는 언제 차를 운행할 수 없을까. 바로 6일, 16일, 26일 사흘 동안이다. 10부제에 동참해야 하는 날들은 이웃항의 차가 10인 등차수열을 이룬다.

수열을 이용하면 일정한 규칙을 갖고 변하는 자연현상이나 사회현상도 쉽게 분석할 수 있다.

수학교과서에서는 수열을 어떤 규칙에 따라 수를 나열한 것이라 정의하고 수열을 이루는 각각의 수를 항이라 한다. 일반적으로 수열은 항에 번호를 붙여 a₁, a₂, a₃,…와 같이 나타낸다. 수열의 제 n항 ${a}_{n}$수식이 n의 식으로 주어지면 n에 1, 2, 3,…을 차례로 대입해 각 항을 구할 수 있으므로 ${a}_{n}$을 수열의 일반항이라고 한다.

그렇다면 2, 4, 6,…로 이뤄지는 수열의 제 n항은 무엇일까? 단순히 생각하면 2n이다. n에 1, 2, 3,…을 차례로 대입하면 각 항 2, 4, 6,…을 구할 수 있으므로 이 수열의 제 n항인 ${a}_{n}$=2n이다.

그러나 ${a}_{n}$수식=(n-1)(n-2)(n-3)+2n이라 놓고 n에 1, 2, 3,…을 차례로 대입하자. 세 번째 항까지 2, 4, 6,…이다. 일반적으로 0이 아닌 상수 k에 대해 ${a}_{n}$수식=k(n-1)(n-2)(n-3)+2n이라 놓고 n에 1, 2, 3,…을 차례로 대입하면 2, 4, 6,…을 얻는다. 그런데 제 4항부터는 k의 값에 따라 모두 다른 수열이 만들어진다. 따라서 이 수열의 경우 무한히 많은 일반항이 존재하는 셈이다.

정답이 하나가 되도록 하려면 어떻게 해야 할까? 문제에서 ‘수열’을 ‘등차수열’로 바꾸면 2, 4, 6,…의 제 n항은 2n이 된다.