교향악 연주회가 시작되기 전 객석은 웅성웅성 떠드는 소리로 가득하다. 이윽고 연주자들이 각자 자리를 잡으면 이번엔 악기들이 ‘떠들기’시작한다. 제멋대로 소리를 내는 것 같지만 악기의 정확한 음정을 잡기 위한 중요한 시간이다.
먼저 환경에 따라 음정 변화가 가장 작은 악기인 오보에가 진동수 440Hz인‘라’음을 낸다. 이 높이의 소리는 오보에에 전혀 손을 대지 않고 불면 나는 소리다. 다른 악기들은 이 오보에의 기준음인‘라’음에 맞춘다. 플루트는 입으로 부는 부분인 헤드를 밀고 빼며, 북은 테두리의 너트를 조인다. 트럼펫은 밸브를 조절해 조율한다.
교향악단의 바이올린, 첼로, 비올라 연주자들은 이들 현악기의 맨 끝에 달린 줄감개로 소리의 높낮이를 조절한다. 줄감개로 줄을 팽팽하게 조이면 소리가 높아지고, 느슨하게 풀어주면 소리가 낮아진다. 어떻게 줄감개로 바이올린의 음정을 조절할 수 있을까.
팽팽해지면 속도가 빨라진다
바이올린 줄을 활로 켜 파동을 양쪽으로 보냈다고 하자. 오른쪽 끝에 도달한 파동은 왼쪽으로 반사하며 뒤따라오던 파동과 겹친다. 반대로 왼쪽 끝에 도달한 파동도 오른쪽으로 반사하며 간섭을 일으킨다. 이런 일이 반복되면‘정상파’가 만들어진다. 정상파를 만든 바이올린 줄은 공명을 일으켰다고 하고, 이때 바이올린은 특정한 음높이의 소리를 만든다.
그럼 음높이는 어떻게 결정될까. 음의 높낮이를 결정하는 요인은 진동수다. 진동수가 많으면 높은 소리가 나고, 적으면 낮은 소리가 난다. 진동수는 파장$λ$와 파동 전달속도$v$의 관계식 $v=fλ$로 결정된다. 그런데 이 식에서 파장은 정상파의 특성 때문에 줄의길이에 따라 특정 값만 갖는다. 정상파에서는 줄의 양쪽 끝이 진동하지 않으므로 반드시 마디가 되기 때문이다. 바이올린 줄의 길이는 정해져 있어 음높이를 조절하려면 줄에서 파동이 전달되는 속도를 조절해야 한다.
그렇다면 바이올린의 줄감개와 파동이 전달되는 속도는 어떤 관계가 있을까? 이것을 차원분석으로 간단히 확인해보자. 파동이 전달되는 줄과 관련된 물리량에는 줄을 잡아당기는 힘($τ$), 단위길이 당 줄의 질량($μ$), 줄의 길이($l$)가 있을 것이다. 여기서 줄의 길이는 파동이 전달되는 속도와 상관 없으므로, $v=C{τ}^{x}{μ}^{y}$로 놓고 양쪽 차원을 비교해보자. $C$는 차원이 없는 상수다.
길이 차원을 $L$, 질량 차원을 $M$, 시간 차원을 $T$라고 하면, $v$의 차원은 $L{T}^{-1}$로 쓸 수 있다. 힘의 차원은 질량 곱하기 가속도의 차원과 같으므로 $ML{T}^{-2}$. 그리고 단위길이 당 줄의 질량의 차원은 $M{L}^{-1}$이다.
정리하면 $L{T}^{-1}={(ML{T}^{-2})}^{x}{(M{L}^{-1})}^{y}= {L}^{x-y}{M}^{x+y}{T}^{-2x}$다. 양 변을 비교해 세 방정식 $x-y=1$, $x+y=0$, $2x=1$을 풀면 $x=\frac{1}{2}$ , $y=-\frac{1}{2}$을 얻는다.
따라서 파동의 속도 $v=C\sqrt{\frac{τ}{μ}}$로 쓸 수 있다. 상수는 뉴턴의 운동법칙을 사용해 계산하면 $C=1$이 나오므로, 파동의 속도 $v=\sqrt{\frac{τ}{μ}}$가 된다.
이제 이 식을 해석해 보자. 바이올린의 줄감개를 감으면 줄을 잡아당기는 힘($τ$)이 커지고 줄을 따라 이동하는 파동의 속도가 빨라진다.$v=fλ$에서 파장은 줄의 길이에 의해 고정돼 일정한 값을 가지므로, 속도가 빨라지면 진동수가 커져 더 높은 소리가 난다.

악기 음정 변화의 원인은 온도!
조율이 끝나고 연주가 시작되면, 지휘자의 지휘에 따라 물 흐르듯 아름다운 화음이 연출된다. 하지만 청중의 체온과 연주회장의 조명 때문에 실내온도는 처음 연주를 시작했을 때보다 높아진다.
다시 연주를 시작할 무렵 교향악단은 처음처럼 조율한다. 온도가 변하면 악기마다 다른 특성 때문에 어떤 악기는 처음보다 소리가 높아지고, 어떤 악기는 처음보다 낮아지기 때문이다.
관악기도 바이올린처럼 공기의 떨림으로 소리를 내파동이 전달되는 속도가 빨라지면 음이 높아진다. 압력에 따른 공기의 부피변화율을 B라고 하고, 공기의 밀도를 $ρ$라고 하면 소리의 속도는 $\sqrt{\frac{B}{ρ}}$ 다. 연주장에서 압력의 변화에 의한 공기의 부피변화율 $B$는 그리 크게 변하지 않아 이에 따른 영향이 거의 없다.
그에 비해 공기 밀도($ρ$)는 온도의 변화에 영향을 많이 받는다. 플루트를 연주하는 곳의 기온이 높아지면 공기밀도가 줄어 파동의 속도가 빨라지고 그 결과 음이 높아진다.
결국 연주회장의 온도가 올라가면 현악기는 금속으로 만든 줄이 나무로 만든 악기몸체보다 더 늘어나기 때문에 줄을 잡아당기는 힘이 약해져 처음보다 낮은 소리가 난다. 반면 관악기는 공기의 밀도가 줄어들어 처음보다 높은 소리가 난다. 온도에 따라 현악기의 줄과 관악기 내부인 공기에서의 파동 속도가 달라지기 때문에 나타나는 현상이다.
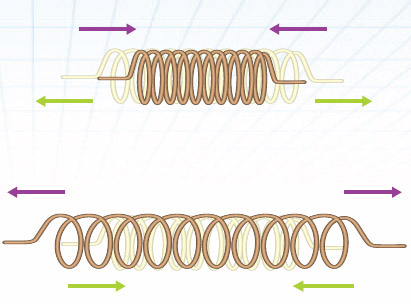
파동은 탄성과 관성의 하모니
파동의 속도 $v=\sqrt{\frac{τ}{μ}}$ 를$v=fλ$에 대입해 정리하면 진동수 $f=\frac{v}{λ}=\frac{1}{λ}\sqrt{\frac{τ}{μ}}$ 가된다. 그런데 여기에는 흥미로운 파동의 비밀이 숨어있다. 파동의 진동수는 탄성을 나타내는 양을 관성을 나타내는 양으로 나누고 제곱근을 취한 값에 비례한다. 이를 어떻게 이해하면 좋을까.
어떤 매질(여기서는 줄)이 탄성과 관성의 성질이 있으면 항상 진동현상이 나타난다. 줄을 잡아당기면 늘어나기 마련이지만 아주 세게 잡아당기지 않는 한 그 형태를 유지한다. 즉 줄은 용수철과 같은 탄성때문에 계속 진동한다. 반면 단위길이 당 질량 $μ$가 갖는 관성은 탄성에 의한 줄의 운동을 방해한다. 이런 탄성과 관성의 밀고 당김의 관계가 파동을 만든다.
이를 용수철의 진동으로 확인해보자. 먼저 용수철 상수가 $k$인 용수철에 질량 $m$인 물체를 달아 진동시킨다. 이때 진동수 공식은 $f=\frac{1}{2π}$다. 여기서도 볼 수 있듯이 진동수는 탄성을 나타내는 용수철 상수 $k$를 관성을 나타내는 질량 $m$으로 나눈 뒤 제곱근을 취한 양에 비례한다.
소리도 마찬가지다. 소리는 공기의 압력변화가 전달되는 것이므로, 이때 관성을 나타내는 양은 공기의 밀도 $ρ$가 된다. 그리고 탄성에 관한 물리량은 공기에 압력을 가했을 때 가한 압력을 줄어든 부피 비율로 나눈양인 부피변화율 $B$로 나타낼 수 있다. 실제로 계산해보면 공기 중에서 전달되는 소리의 속도는 $\sqrt{\frac{B}{ρ}}$다.
빛의 경우는 어떨까. 빛은 특이하게 매질이 없어도 전달되는 전자기파다. 매질이 없는데도 전자기파의 진동수를 탄성과 관성으로 표현할 수 있을까?
매우 이상하게 들리겠지만 전자기파도 탄성과 관성으로 표현할 수 있다. 빛의 속도 $c=\frac{1}{\sqrt{{ε}_{0}{μ}_{0}}}$로 나타낸다. 여기서 ${ε}_{0}$는 진공의 유전상수로 전하의 힘을 전달하는 정도를 나타내는 상수다. 그리고 ${μ}_{0}$는 진공의 투과상수라고 부르는 값으로 전류에 의해 유도되는 자기장이 얼마나 잘 퍼지는지에 대한 척도다.
전자기파는 전기장과 자기장이 서로를 유도하며 진행하는 파동이다. 파동의 속도는 탄성을 나타내는 양을 관성을 나타내는 양으로 나누고 제곱근을 취한 값에 비례하므로, 전기장은 관성의 효과 ${ε}_{0}$를, 자기장은 탄성의 효과 $\frac{1}{{μ}_{0}}$를 만든다고 볼 수 있다.
이와 같이 모든 진동현상은 관성과 탄성의 효과로 설명할 수 있다.











