d라이브러리

어릴 적 비눗물을 그릇에 담고 빨대로 불어 비눗방울을 공중에 뿌리는 놀이를 해보지 않은 사람은 아마도 없을 것이다. 무지개 빛을 뿜는 작은 물방울의 현란한 움직임에 정신이 팔려 불고 또 불던 기억이 새롭다. 요즘 결혼식장에서 기계로 뿜어대는 비눗방울의 양에는 못미치지만, 사람의 숨을 담아 허공 가득히 비눗방울을 만들어내던 놀이는 아름다운 것이 얼마나 쉽게 사라지는지 처음 알게 해준 경험이었다.

그러나 비눗방울의 진정한 아름다움은 그것이 터져 버리고 난 후에도 남아있다. ‘극소곡면’이라는 이름으로….

다음과 같은 상황을 생각해보자.

바다 속에 유전(油田)이 세개 있다. 그리고 유전에서 생산된 석유를 한곳으로 모으기 위해서 ‘송유관’을 만들려고 한다. 경비를 절약하기 위해서는 관의 길이를 가능한 짧게 해야 한다. 유전들을 어떻게 연결하면 좋을까.

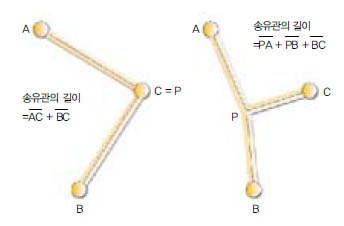
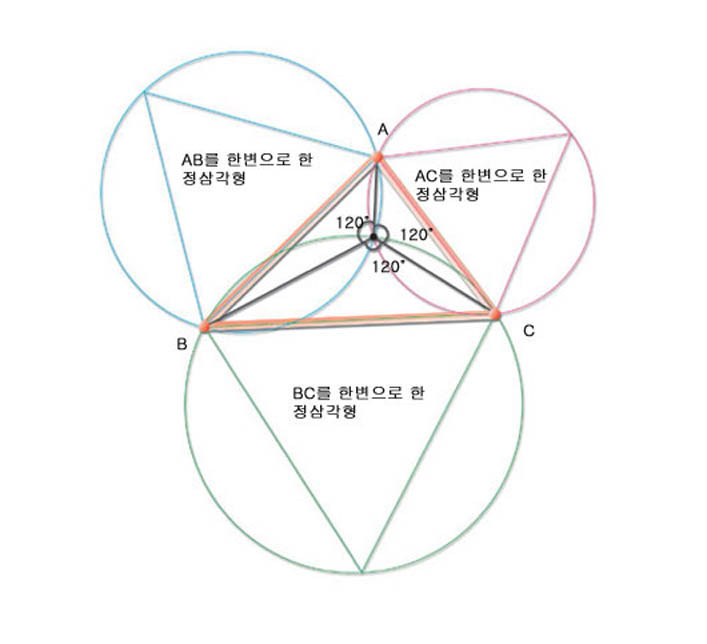
세 유전이 삼각을 이루고, 그 위치가 A, B, C 라고 하자. 그리고 석유를 모으는 곳을 P라고 하자. 만약 P가 유전 중 하나라면, 이때 송유관의 길이는 A와 C 사이의 거리(AC)와 B와 C사이의 거리(BC)의 합이다. 또는 세 유전이 아닌 다른 지점에 석유를 모으는 경우라면, 이때 관의 길이는 PA + PB + PC이다. P의 정확한 위치는 어디일까.

이 문제를 접어두고 다른 상황을 생각해보자.

어떤 지역에 문화센터를 지으려고 한다. 지역 주민들이 모두 편하게 다닐 수 있도록 하려면 여러 점들을 고려해야겠지만 여기에서는 주민들이 문화센터로 오는 거리의 합이 가장 짧게 되는 점을 최우선으로 생각해보자. 이 지역을 5개의 지구로 나눌 수 있다면 송유관처럼 5개의 지구와 문화센터를 잇는 거리의 길이가 가장 짧은 지점을 찾는 문제로 생각할 수 있다.

이처럼 거리의 합이 최소인 점을 찾는 문제는 프랑스의 수학자 페르마(1601-1665)에 의해서 제기됐다. 그래서 페르마의 이름을 따 이 점을 ‘페르마 점’(Fermat Point)이라 부른다. 이 문제는 여러 수학자들의 지속적인 노력으로 해결됐다.


비눗방울들이 1백20° 구조 띤 이유

재미있게도 이 문제의 답은 비누막에서 찾을 수 있다. 비누막은 공기에 닿는 넓이가 가장 작게 되도록 퍼지는 성질을 갖는다. 이를 응용하면 길이가 가장 짧은 연결점을 찾을 수 있다.

다각형이나 원 모양의 철사줄 또는 플라스틱 막대를 비눗물에 담갔다가 빼내면 비누막이 생긴다. 이때 생긴 비누막은 철사줄이나 플라스틱 막대를 둘러싼 평면이다. 이것이 철사줄 둘레를 따라 생길 수 있는 곡면 가운데 가장 표면이 작은 경우다. 표면장력이 작용한 것이다. 따라서 평면은 비누막 중에서 가장 표면이 작은 곡면(극소곡면)인 셈이다.

비누막은 극소곡면을 따른다. 비눗방울들이 서로 만난 부분에서 곡선이 형성되는데 이 곡선을 따라 비눗방울들은 서로 1백20°의 각도로 만난다. 이 각도로 만나야 비누거품의 넓이가 최소가 되기 때문이다.

1백20°의 구조는 정육각형 모양의 벌집, 화산에 의해 생성된 현무암 기둥, 잠자리 날개와 같이 자연에서 수없이 발견된다. 이 성질을 이용해 지붕을 만들면 그 구조가 단단하고 비용도 적게 든다. 때문에 건축에서 실제로 이용되기도 한다.

송유관이나 문화센터 문제가 바로 이 1백20° 구조로 해결된다. 세 유전 A, B, C에서 거리합을 최소로 하는 석유 저장 장소 P는 삼각형 ABC 세 변 위에 각각 정삼각형을 그렸을 때, 세 정삼각형의 외접원의 교점이 페르마 점이다. 삼각형의 세 꼭지점과 페르마 점을 잇는 세 선분이 이루는 각이 모두 1백20°이다. 사각형, 오각형의 경우에서도 꼭지점을 잇는 거리의 합이 최소인 점은 1백20° 구조를 이룰 때 찾을 수 있다.

이를 비누막 실험에서 확인해보자.