d라이브러리

벌은 수많은 알과 꿀을 저장하기 위해 육각기둥의 집을 짓는다. 그런데 왜 하필 육각기둥일까. 그 까닭을 삼각형, 사각형, 육각형의 도형문제로 풀어본다.


인간생활의 기본적인 3요소 중 하나인 집. 하지만 인간뿐 아니라 새나 곤충을 비롯한 모든 생명체에게 안식처는 중요하다. 때문에 사람만이 집을 짓고 사는 것은 아니다. 나뭇가지를 물어다가 짓는 새, 자신의 몸에서 생산되는 줄로 엮어 만드는 거미, 땅 속에 흙을 파서 만드는 개미 등 생명체는 제각기 독특한 방식으로 집짓기를 한다. 이 중 육각기둥의 독특한 구조를 지닌 벌집이 가장 튼튼하고 과학적이라고 얘기한다. 벌은 어떻게 이 독특한 집을 지을까.

여왕벌은 꿀을 찾아 날아다니다가 새로운 집을 지을만한 곳을 찾아내면 곧바로 집짓기를 시작한다. 벌집의 재료는 식물 껍질에 붙어있는 섬유질이다. 벌은 날카로운 턱으로 식물에서 섬유질을 뜯어낸 다음 그 섬유질에 자신의 침을 섞어서 걸쭉해질 때까지 잘게 씹는다. 그리고 부지런히 입을 놀려 육각형의 방을 지어나간다. 방이 얼마쯤 만들어지면 크기가 2mm 정도인 알을 방 한칸에 하나씩 낳는다.

벌집은 수만마리 벌의 생활 보금자리이다. 작은 방은 꿀벌, 큰방은 수펄들이 자리잡고 봄에는 여왕벌이 자라는 방이 따로 만들어진다. 그런데 수많은 작은 방으로 이뤄진 벌집은 그 모양이 육각형으로 매우 독특하다.

벌은 왜 육각형으로 집을 지을까.

자연은 우리가 생각하는 것 이상으로 효율적인 시스템으로 설계돼 있다. 집단생활을 하는 것으로 알려진 벌에게서도 이러한 증거를 발견할 수 있다. 벌이 육각형 모양으로 집을 짓는 것도 효율성을 구현하는 예이다. 이 원리를 2가지 측면으로 나눠 생각해보자.

먼저 집에 수많은 방을 만들 때 어떤 모양으로 만드는 것이 좋은지를 생각해보자. 공간을 효율적으로 사용하고 튼튼한 구조를 가지려면 방이 빈틈없이 이어져야 한다. 그런데 방의 모양이 정다각형일 때 겹치지 않고 빈틈없이 평면을 채울 수 있으려면 방의 모양이 어떠해야 할까. 답은 세가지. 정삼각형, 정사각형, 그리고 정육각형뿐이다.

정n각형의 한 내각의 크기는 $\frac{(n-2)×180}{n}$ 이다. 정n각형 m개로 평면을 빈틈없이 겹치지 않게 채우려면 한 꼭지점에 모이는 각이 360°를 이뤄야 한다. 따라서 $\frac{(n-2)×180}{n}$×m = 360°이다.

이 식을 정리하면
mn - 2m - 2n = 0
→ (n - 2)(m - 2) = 4

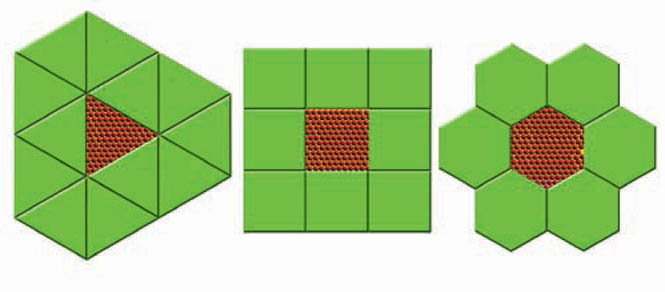
m, n은 자연수이므로 위의 식을 만족하는 n, m은 (3, 6), (4, 4), 그리고 (6, 3)이다. 따라서 정삼각형 6개, 정사각형4개, 정육각형 3개로 평면을 빈틈없이 채울 수 있다(그림).

이 중에서 벌은 왜 하필 육각형을 선택했을까. 이는 최소의 비용으로 최대의 효과를 얻기 위함이다. 바로 최소의 재료로 최대의 공간을 얻을 수 있는 것. 그러면 정삼각형, 정사각형, 정육각형 모양의 방을 지을 때 같은 분량의 재료로 가장 넓은 공간을 만들 수 있는 경우는 무엇일까.

둘레의 길이가 모두 12인 정삼각형, 정사각형, 그리고 정육각형을 생각해보자.

이 경우 정삼각형은 한변의 길이가 4이므로 정삼각형의 넓이는 $\frac{\sqrt{3}}{4}$×${4}^{2}$≒ 6.93,정사각형은 한변의 길이가 3이므로 정삼각형의 넓이는 ${3}^{2}$= 9,그리고 정육각형은 한변의 길이가 2이므로 정육각형의 넓이는 6($\frac{\sqrt{3}}{4}$×${2}^{2}$)= 6$\sqrt{3}$≒ 10.39이다. 따라서 일정한 양의 꿀을 저장하기 위한 집을 만들 때 재료가 가장 적게 들어가려면 정육각형 모양으로 지어져야 한다.

정육각형 모양의 구조물은 빈틈이 없으면서 매우 튼튼한 형태가 된다. 실제로 튼튼한 구조물을 만들 때 그 내부를 육각형 구조로 만드는 경우가 많다. 지름이 6m 정도인 큰 망원경을 만들 때 그 받침대의 내부에, 그리고 비행기의 무게를 줄이고 재료도 절약하기 위해 비행기 구조물 자체에 벌집식 구조가 사용된다. 이런 구조물은 속이 비고 두끝이 금속관으로 고정되기 때문에 속이 비지 않은 구조물보다 강도가 높고 무게도 가벼우며 소리나 열을 격리시키는 효과도 좋다고 알려져 있다.


[ 체험하는 수학 ] 어느 공간이 가장 넓을까

| 준비물 | 구슬, 칼, 자, 두꺼운 종이.

| 실 험 |

1. 두꺼운 종이로 정삼각형 12개, 정사각형 9개, 그리고 정육각형 6개를 만든다. 이때 정삼각형, 정사각형, 정육각형 한변의 길이비가 4 : 3 : 2가 되도록 한다.
 

2. 정삼각형 12개, 정사각형 9개, 그리고 정육각형 6개 각각을 가운데가 비도록 하고 서로 가까이 붙여놓는다.

3. 세종류의 판 가운데 빈부분에 구슬을 최대한 많이 넣는다.

4. 각 판에 들어간 구슬의 개수를 세어본다. 정삼각형보다 정사각형에, 그리고 정사각형보다 정육각형에 더 많은 구슬이 들어간다는 것을 확인할 수 있다.