d라이브러리

2000년 상반기에는 벤처열풍이 불었다. 순식간에 엄청난 돈을 벌 것 같았기 때문이다. 벤처열풍과 같은 예 속에는 누구나 백만장자가 되고 싶은 사람들의 욕망이 숨겨져 있다.여러분도 백만장자가 되고 싶은가. 그렇다면 지뢰찾기 게임을 잘 들여다보라.

개인용 컴퓨터의 대부분에 깔려있는 유명한 지뢰찾기 게임. 지뢰가 터질 때 낭패감을 느끼기도 하지만, 끝까지 지뢰를 다 찾아냈을 때 성취감을 맛보는 게임이다. 이런 게임 속에 12억원이 숨어있다니…. 그 내막을 살펴보자.

미국 매사추세츠주 케임브리지 소재 클레이 수학연구소에서 7대 수학난제를 해결하는 사람에게 한문제 당 12억원의 상금을 주겠다고 2000년 5월 발표했다. 전세계적인 관심 속에 최근 우리나라에서도 이에 대한 설명회가 개최됐다.

7대 수학난제 중 하나

2000년 12월 1일 서울대 상산수리관에서 열린 수학난제 설명회에는 수많은 사람들이 모여들었다. 클레이 수학연구소가 제시한 7대 수학난제 중 4개에 대해 4명의 전문가들이 각각 하나씩 릴레이식 해설 강연을 했다. 그런데 여기서 소개된 4문제 중 하나가 유명한 지뢰찾기 게임과 관련이 있다. 다름아닌 P 대 NP 문제. 영국 버밍햄대의 리차드 카예 박사가 지뢰찾기 게임과 P 대 NP 문제의 연관성에 대한 논문을 발표했던 것이다.

먼저 지뢰찾기 게임을 살펴보자. 게임이 시작되면 바둑판처럼 생긴 판이 등장한다. 게임판은 여러개의 타일처럼 생긴 사각형으로 이뤄지는데, 어떤 사각형 뒤에는 지뢰가 숨어있다. 게임의 목표는 지뢰를 터뜨리지 않고 게임판에 숨어있는 지뢰를 모두 찾아내는 것이다. 처음에는 아무 사각형이나 열어야 하는데 지뢰가 든 사각형을 선택하면 바로 게임 끝. 그렇지 않은 경우 사각형 뒤에는 숫자가 나타난다. 이 숫자는 인접한 8개의 사각형에 숨어있는 지뢰의 수를 의미한다.

이제 이 숫자정보를 이용해 다음 사각형을 연다. 물론 이때도 지뢰가 터지거나 인접한 지뢰의 수를 알려주는 숫자가 나온다. 또한 지뢰가 있다고 예상되는 사각형에는 깃발을 꽂으면 된다. 이런 식으로 게임을 진행해 아무 일 없이 지뢰를 다 찾으면 임무완수.

어렵다는 것을 증명하기 어려운 문제

이제 지뢰찾기 게임과 관련된 P 대 NP 문제 속으로 들어가보자. 여러분은 알고리듬이라는 단어를 들어본 적이 있을 것이다. 흔히 컴퓨터에서 어떤 문제를 풀기 위해 거치는 단계적인 과정을 말한다. 컴퓨터계산의 주안점은 어떤 알고리듬이 주어진 문제를 푸는데 얼마나 효과적인가 하는 것이다. 다시 말하면 답을 구해내는데 필요한 계산시간이 얼마나 걸리는가의 문제다.

주어진 문제를 크게 분류한다면 쉬운 문제, 어려운 문제, 판정이 불가능한 문제의 세가지로 나눌 수 있다(여기서 판정이 불가능한 문제는 생각하지 말자). 어려운 문제는 답을 찾는데 시간이 무척 많이 걸리는 문제다. 일상생활 속에서도 ‘기하급수적’이라는 용어가 곧잘 사용되는데 예를 들어 숫자가 1, 2, 4, 16, 32, 64,… 2n 등으로 늘어가는 경우 기하급수적 증가라고 말할 수 있다. 답을 구하는데 기하급수적인 시간이 걸리는 문제가 바로 어려운 문제다.

쉬운 문제는 당연히 답을 얻는데 시간이 별로 걸리지 않는 문제다. 다시 말해 답을 찾는데 기하급수적인 시간이 아닌 ‘다항 시간’(polynomial time)이 걸리는 문제가 쉬운 문제, 즉 P 문제인 것이다. 다항 시간이란 1, 4, 9, 16, 25,… n2과 같은 형태로 걸리는 시간이다.

P 문제는 컴퓨터가 효과적으로 해결할 수 있다. 하지만 어려운 문제는 어떤 알고리듬을 사용하든 컴퓨터가 답을 내는데 진저리나게 오래 걸린다.

예를 들어 여러개의 숫자를 오름차순이나 내림차순으로 배열하는 문제는 쉬운 문제다. 엄청난 분량을 순서대로 배열하는 일을 상업용 데이터베이스 프로그램에서 효과적으로 소화할 수 있는 이유다. 반면에 세일즈맨이 여러 도시를 방문하는데 가장 효과적인 길을 찾아내는 ‘세일즈맨 여행 문제’는 어려운 문제라고 믿고 있다. 왜냐하면 세일즈맨이 방문해야 할 도시가 10개라도 선택가능한 길은 10×9×8…3×2×1의 수가 있을 만큼 엄청난데, 더 많아지면 정말 해결하기가 어렵기 때문이다.

하지만 이렇게 어려운 문제가 실제 어렵다고 하는 사실은 완벽하게 증명된 적은 없다. 증명하는 과정에도 수많은 알고리듬이 있고 어떤 알고리듬도 기하급수적인 시간이 걸린다는 점을 보여야하는데 이 역시 불가능하기 때문이다.
 

어려워보이는 문제, 사실 쉬운 문제인가
 

어려운 문제를 잘 들여다보면 문제를 푸는데 어렵지만 풀이가 올바른지를 판단하기는 쉬운 문제가 있다. 이런 문제를 어려워보이는 문제, 즉 NP 문제라고 한다. 조각맞추기 게임이 대표적인 예다. 실제 해본 사람은 알겠지만 수천조각을 완성하려면 주어진 그림이 있고 조각맞추기에만 전념하더라도 며칠씩이나 걸린다. 조각맞추기 경우에는 수많은 조각을 맞추기 어렵지만 잘 맞춰져는지를 판단하기는 쉽다. 완성된 그림을 모르더라도 조각과 조각 사이가 제대로 맞았는지만 판단하면 되기 때문에 이를 확인하는 시간은 조각 수에 비례하는 정도밖에 걸리지 않는다.

이런 NP 문제들 중에는 NP 완비문제라는 그룹이 있다. 모든 NP 완비문제들은 다항 시간 내에 대표적인 NP 완비문제인 SAT 문제로 바꿀 수 있다. SAT 문제는 일종의 논리회로와 관련된 문제다. 논리회로는 AND(논리곱), OR(논리합), NOT(부정)과 같은 연산자로 적절히 결합돼 구성된다. SAT 문제는 주어진 논리회로에 대해 출력값 T(참)를 얻을 수 있는 입력값을 선택할 수 있는지를 묻는 것이다.

4개의 문이 달린 자동차의 실내등을 생각해보자. 자동차 실내등이 꺼지는 결과(출력값 T)가 나오려면 어떤 상황(입력값)이 주어져야 하는가. 4개의 자동차문 중의 어떤 하나라도 열려 있으면 꺼지지 않는다. 따라서 이 경우는 AND 연산자로 연결된 간단한 문제인데 4개의 문이 모두 닫히면 해결된다. 하지만 좀더 복잡하게 얽힌 경우의 SAT 문제라면 답을 얻기 쉽지 않다.

NP 완비문제가 왜 중요할까. NP 문제들은 풀이하는데 비슷한 시간이 걸린다고 알려져 있다. 따라서 NP 완비문제를 다항 시간 내에(쉽게) 풀 수 있다면 다른 모든 NP 문제들도 다항 시간 내에 풀 수 있다고 할 수 있다. NP 완비문제는 SAT 문제와 같이 다루기 쉽기 때문에 NP 완비문제가 쉽게 풀리는지 여부를 따지면 된다.

그러면 12억원이 걸린 P 대 NP 문제는 무엇일까. 이 문제는 P 문제가 NP 문제와 같은지를 증명하는 것이다. 물론 P 문제와 NP 문제가 다르다는 사실을 증명해도 된다. 얼핏 보기에 쉬운 문제인 P 문제는 어려워보이는 문제인 NP 문제와 달라 보이지만 아직 증명이 안돼 있기 때문이다.

모순없는 게임판을 쉽게 만들라
 

이제 지뢰찾기 게임과의 연관성을 살펴보자. 지뢰찾기 게임의 일관성문제를 생각할 때 이런 연관성이 등장한다. 게임의 일관성문제는 지뢰를 찾는 것이 아니라 지뢰찾기 게임을 논리적으로 일관되게 구성할 수 있는지를 결정하는 것이다. 예를 들어 게임판의 모서리에서 6이라는 숫자가 나왔다고 하자. 하지만 이 6이라는 숫자는 모서리의 사각형 둘레에 존재하는 사각형의 개수가 3개뿐이기 때문에 논리적 일관성이 깨진 것이다. 프로그래머의 실수다.

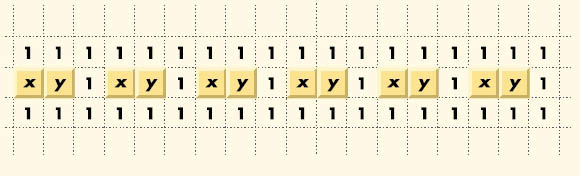
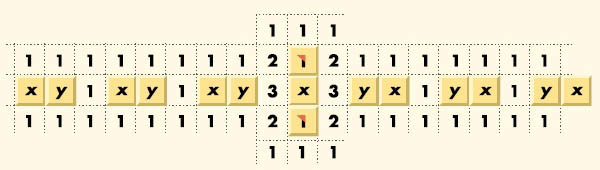
카예 박사가 증명한 사실은 SAT 문제를 다항 시간 내에 지뢰찾기 게임으로 바꿀 수 있다는 것이다. 즉 지뢰찾기 게임이 NP 완비문제라는 것이다. 물론 이 변환의 경우 지뢰가 있는 사각형은 T(참)를 나타내고 지뢰가 없는 사각형은 F(거짓)를 나타낸다. 카예 박사는 지뢰찾기 게임에서 논리연산자를 연결할 수 있는 ‘연결끈’을 고안해냈다(그림1). 이때 x라고 쓰인 사각형과 y라고 쓰인 사각형은 서로 반대값을 가진다. 다시 말하면 x의 위치에 지뢰가 있으면(T면), y의 위치에는 지뢰가 없고(F고), x에 없으면 y에 있다. 이 연결끈의 역할은 길이 방향으로 신호(T 또는 F)를 전파하는 것이다.

또한 카예 박사는 지뢰찾기 게임에서 모든 논리연산자를 구현해냈다. 예를 들어 NOT 연산자의 경우를 보자(그림2). 연결끈 중간에 그림과 같은 숫자의 묶음을 집어넣으면 x와 y의 위치가 바뀐다. 따라서 각각의 값(T 또는 F)이 반대가 돼 중간에 들어간 숫자 묶음은 정확하게 논리회로의 NOT 역할을 한다. 다른 경우는 더 복잡해지지만 카예 박사는 자신의 논문에서 모두 제대로 구현했다.

그렇다면 12억원의 상금을 타려면 어떻게 해야 할까. 지뢰찾기 게임도 NP 완비문제이므로 지뢰찾기 게임만 잘 들여다보면 된다. 다시 말하면 지뢰찾기 게임을 일관성있게 구현할 수 있는 알고리듬을 다항 시간 내에(쉽게) 찾을 수 있으면 모든 NP 문제는 다항 시간 동안 답을 구할 수 있는 것이다. 즉 P 문제와 NP 문제가 같다는 사실을 증명한 것이다. 반대로 지뢰찾기 게임의 일관성문제에 다항 시간 동안 얻을 수 있는 답이 존재하지 않는다는 사실을 증명하면 P 문제와 NP 문제가 다르다는 사실을 증명하는 것이다.

지뢰찾기 게임 속에 12억원의 상금이 걸려있지만 이 문제를 풀기는 쉽지 않다. 게임판이 조그만 경우뿐만 아니라 굉장히 큰 경우에도 일관성있는 게임판을 만들 수 있는 알고리듬을 찾아야 한다. 물론 쉽게. 더욱이 클레이 수학연구소에서는 제시된 답안이 타당한지를 판단하기 전에 저명한 저널에 실려야만 하고 2년 동안 수학계에서 널리 받아들여져야 한다는 단서를 달고 있다.