d라이브러리

실생활에서는 무리수가 필요 없다고 하지만, A4 용지, B4 용지와 같은 종이의 재단이나 음악의 음정 이론에는 무리수가 쓰인다(과학동아 1999년 7월호와 10월호 ‘생활 속의 수학 이야기’ 참조). 원주율 π와 자연 로그의 밑 e(≒2.718)에서 알 수 있듯이, 수학에서는 무리수가 매우 중요한 역할을 한다. 이 외에도 누구나 알고 있지만 쉽게 지나쳐버린 무리수에는 ‘황금비’도 포함돼 있다. 다음 그림과 같이 선분 AB 위의 점 C에 대해서, 긴 선분 AC에 대한 짧은 선분 CB의 비가 전체 선분 AB에 대한 긴 선분 AC의 비와 같은 때, 즉 $\frac{\overline{CB}}{\overline{AC}}$ = $\frac{\overline{AC}}{\overline{AB}}$일 때, 선분 AB는 점 C에 의해 ‘황금분할’됐다고 한다.

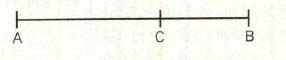
그래서 $\overline{AB}$ = 1, $\overline{AC}$ = x 라고 하면, 다음을 얻는다.
$\frac{1-x}{x}$ = $\frac{x}{1}$, x²+ x - 1 = 0, x = $\frac{\sqrt{5}-1}{2}$
이 수 $\frac{\sqrt{5}-1}{2}$ ≒ 0.618 또는 이 수의 역수 $\frac{1}{x}$ = $\frac{\sqrt{5}+1}{2}$ ≒ 1.618 을‘황금비’라고 한다.

폭에 대한 길이의 비가 황금비인 ‘황금직사각형’은 대부분의 사람의 눈에 가장 아름답게 보인다는 심리학적인 실험 결과도 있다. 황금비와 황금직사각형은 고대부터 건축과 공예에 활용됐다. 파르테논 신전에서 신전의 높이에 대한 폭의 비가 황금비라는 것은 이미 알려진 사실이다. 그 뒤 많은 미술가들이 이를 의도적으로 활용한 경우도 찾아볼 수 있다.

피보나치 수열과 인체의 비례

피보나치 수열은 다음과 같다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …, m, n, m+n, …
그런데 피보나치 수열에서 연속한 항들의 비를 택하면 다음과 같은 수열을 얻는다.

$\frac{1}{1}$ (=1), $\frac{2}{1}$ (=2), $\frac{3}{2}$ (=1.5), $\frac{5}{3}$ (≒1.667), $\frac{8}{5}$ (=1.6), $\frac{13}{8}$ (≒1.625), $\frac{21}{13}$ (≒1.615), $\frac{34}{21}$ (≒1.619), $\frac{55}{34}$(≒1.618), $\frac{89}{55}$(≒1.618), …

놀랍게도, 이 수열의 극한은 실제로 황금비 $\frac{\sqrt{5}+1}{2}$ 이다. 피보나치 수열을 자연에서 쉽게 찾아볼 수 있기 때문에, 자연과 황금비 사이에도 어떤 관계가 있을 것이라고 추측된다.

황금비는 여러 가지 다양한 상황에서 나타난다. 그렇다면 우리의 몸에서도 황금비를 찾을 수 있을까. 레오나르도 다 빈치는 인체의 비례를 광범위하게 연구했고, 자신의 그림에 황금비를 이용했다(그림1).

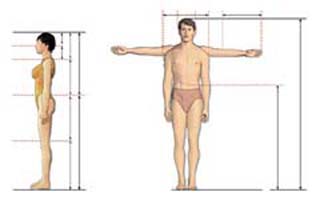
(그림 2)는 현재 중학교 3학년의 한 교과서에 실린 것과 유사하게 그린 것이다. 이 그림에 대해 다음과 같은 설명이 있다. “배꼽의 위치가 사람의 몸 전체를 황금분할하고, 어깨의 위치가 배꼽 위의 상반신을, 무릎의 위치가 그 하반신을, 코의 위치가 어깨 위의 부분을 각각 황금분할할 때, 가장 조화롭고 아름답다고 한다.”

이상적인 운동 선수의 인체를 보여주는 (그림 3)에서도 배꼽의 위치가 몸 전체를 황금분할하고 있다. 또 어깨 폭에 대한 팔 길이의 비도 황금비를 이룬다. ($\frac{CB}{AC}$, $\frac{AB}{CB}$, $\frac{bc}{ab}$ 는 황금비) 하지만 많은 사람이 이 말에 동의하지 않을 수도 있다. 그렇다면 주변 사람들의 인체 비례를 측정해 보는 것은 어떨까. 뉴욕시에 살고 있는 롱크(F. A. Lonc)는 여자 65명의 키와 배꼽까지의 높이를 재서 이를 확인했다고 한다. 그는 여자의 키를 배꼽까지의 높이로 나눈 값의 평균이 1.618이었다고 발표했다.

황금비의 연분수 전개

분자가 1인 분수들이 포개진 형태로 나타나는 분수를 ‘(단순) 연분수’라고 한다. 분수 $\frac{57}{17}$ 을 연분수로 나타내면 다음과 같다.

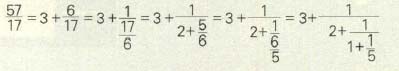
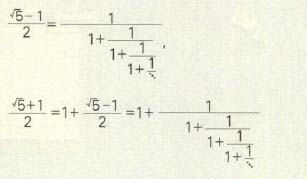
일반적으로 유리수는 유한 연분수로 표현되고 무리수는 무한 연분수로 표현된다. 황금비 $\frac{\sqrt{5}-1}{2}$ 을 연분수로 나타내기 위해서,
이를 근으로 갖는 이차 방정식을 다음과 같이 나타내자.

${x}^{2}$+ x - 1 = 0, x² + x = 1, x(x+1) = 1,

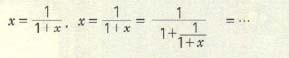
이와 같이, 분모에 있는 x 를 $\frac{1}{1+x}$로 계속해서 바꿀 수 있으므로
무리수인 황금비 $\frac{\sqrt{5}-1}{2}$ 과 $\frac{\sqrt{5}+1}{2}$ 은 다음과같이 대단히 규칙적이고 단순한 연분수로 표현된다.