d라이브러리

일정한 크기의 종이를 반으로 계속 자르다 보면 A1, A2, A3, A4 용지를 만날 수 있다. 이들은 어떤 규칙으로 만들어졌을까.

복사용지를 포함해 공문서 등에 가장 많이 사용되고 있는 종이가 바로 A4 용지다. A4 용지의 규격은 297mm×210mm이다. 단순하게 300mm×200mm로 정하면 훨씬 편했을 텐데 왜 이렇게 복잡한 수치가 쓰였을까. 게다가 A4 용지는 우리 눈에 가장 아름답게 보인다는 황금비를 이루지도 않는다. 황금비는 (1 +$\sqrt{5}$ ) / 2≒1.618인 반면, A4 용지의 폭에 대한 길이의 비는 약 1.414이다.

종이의 경제학

일상 생활에서 사용되는 종이는 제지소에서 만든 큰 규격의 전지를 절반으로 자르고 또다시 절반으로 자르는 과정을 반복하면서 만들어진다. 그런데 이렇게 절반으로 자르다보면, 원래의 규격과 다른 모양이 될 수 있다.

예를 들어 300mm×200mm와 같이 폭에 대한 길이의 비가 1.5인 종이를 절반으로 자르면, 200mm×150mm 크기로 만들어지고 이때의 비는 1.333(4/3)이다. 1.333의 비를 가진 직사각형은 1.5의 비를 가진 처음 종이에 비해 뭉툭해 보인다. 이런 종이를 실생활에 필요한 용도로 이용하기 위해서는 일부를 잘라내어 보기 좋은 형태로 만들어야 한다. 그렇게되면 아까운 종이와 펄프를 낭비하게 된다.

독일공업규격 위원회(Deutsche Industrie Normen)는 큰 종이를 잘라서 작은 종이를 만드는 과정에서 종이의 낭비를 최소로 줄일 수 있는 종이의 형태와 크기를 제안했다. 적절한 규격을 선택했을 때, 타자지의 절반을 그대로 편지지로 사용하고 편지지의 절반을 그대로 메모지로 사용한다면 종이를 많이 절약할 수 있을 것이라고 여겼다. 이렇게 해서 등장한 것이 A4 용지다.

문제는 닮은꼴

절반으로 자르는 과정에서 만들어지는 종이를 그대로 사용하기 위해서는 어떻게 해야 할까. 우선 전지의 규격이 보기 좋아야하고, 이를 절반으로 자르고 또다시 절반으로 자른 작은 종이들이 전지의 규격과 같으면 바람직하다. 수학적으로 말하면 서로 닮은꼴이어야 한다는 얘기다.

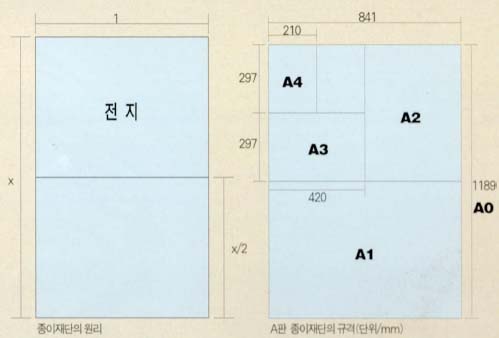
전지의 길이 대 폭의 비를 x : 1이라고 하자. 그러면 이것을 절반으로 자른 종이의 길이 대 폭의 비는 1 : $\frac{x}{2}$ 이다. 두 직사각형이 서로 닮은꼴이므로 비례식 x : 1 = 1 : $\frac{x}{2}$ 가 성립하고, 이로부터 이차 방정식 ${x}^{2}$=2를 얻는다. 그래서 x=$\sqrt{2}$이다. 이렇게 전지의 폭에 대한 길이의 비를 $\sqrt{2}$로 택하면, 반으로 자르는 과정에서 이 비가 항상 유지된다. $\sqrt{2}$는 황금비는 아니지만 눈으로 보아서 그렇게 큰 차이가 나지 않는다. 이렇게 도형의 닮은꼴, 비례식, 이차 방정식, 무리수 등의 수학적 개념이 실생활에 유용한 종이의 재단에 이용된다.

A4와 B4의 차이

앞에서 A4 용지의 폭에 대한 길이의 비는 약 1.414였다. 눈치챘겠지만, 이 값은 실제로 $\sqrt{2}$를 가리킨다. 단지 제조 과정에서 편의를 위해 근사값을 택했을 뿐이다. 그런데 왜 297mm×210mm일까. A4 용지의 전지를 A0라고 하는데, A0의 규격은 1189mm×841mm이다. 더 복잡한 수치다. 그런데 A0 용지의 넓이를 계산해보면 999949mm²임을 알 수 있다. 이는 1000000mm², 즉 1m²의 근사값이다. A0는 폭에 대한 길이의 비가 $\sqrt{2}$이고 넓이는 1m²가 되도록 만든 종이이다. 이를 절반으로 자르는 과정에서 A1, A2, A3, A4 등의 ‘에이(A)판’ 용지가 만들어진다.

B4와 B5 용지도 많이 사용된다. 이런 종이도 A판과 같은 원리로 만들어진다. 전지 B0의 폭에 대한 길이의 비는 $\sqrt{2}$이고 넓이는 1.5m²가 되도록 규격을 1456mm×1030mm로 정했다. 이를 절반으로 자르는 과정에서 B1, B2, B3, B4, B5 등의 ‘비(B)판’이 만들어진다.

A판과 B판의 모든 용지가 서로 닮은꼴(A0와 B0의 닮음비는 $\sqrt{1.5}$이기 때문에, 적절한 비율로 확대하거나 축소해서 다른 용지에 복사할 수 있는 또다른 이점이 있다.

A판과 B판의 폭에 대한 길이의 비는 우리 눈에 가장 아름답게 보인다는 황금비는 아니다. 그렇다고 주변에서 황금비를 이루는 종이나 책을 찾아보기 쉬운 것도 아니다. 실제로 황금비를 이루는 직사각형을 그려보면 이것이 매우 길다는 느낌을 갖게 될 것이다. ‘수학적으로’ 만들어진 종이인 A판과 B판이 현대적 황금비가 아닐까.

$\sqrt{2}$는 입에 담지 못할 수

한때 $\sqrt{2}$는 환영받지 못한 수였다. '수는 만물을 지배한다'고 역설했던 피타고라스(기원전 572?-492?)가 말했던 '수'는 자연수를 뜻했다. 그리고 자연수의 비로 표현할 수 있는 양의 유리수는 분명히 '수'의 지배를 받는다. 당시는 물론 17세기까지도 '수'는 양의 유리수를 의미했다. 그런데 피타고라스가 증명한 피타고라스의 정리에 의해 직각을 낀 두 변의 길이가 1인 직각 삼각형의 빗변의 길이는 $\sqrt{2}$가 돼야 한다. 그러나 그는 $\sqrt{2}$가 자연수의 비로 표현되지 않는다는 충격적인 사실을 알게됐다. 자신의 철학에 반하는, 즉 자연수의 지배를 받지 않는 수학적 대상이 존재했던 것이다. 그래서 그는 이를 '입에 담지 못할 수' (alogos)라고 불렀고, 비밀로 유지하려고 노력했다. 이를 외부에 발설한 제자를 수장시켰다는 이야기도 있다.

피타고라스 시대에는 소수 표현 방법이 없었다. 소수를 이요하면, $\sqrt{2}$도 분명히 자연수로 표현되기 때문에, 피타고라스의 '(자연)수는 만물을 지배한다'는 말이 거짓은 아니다.