d라이브러리

신은 주사위 놀이를 하지 않는다며 양자론의 확률적인 해석을 거부했던 아인슈타인. 그렇지만 그는 양자론이 성립하는데 중요한 노릇을 한다.

20세기의 과학자 가운데 아인슈타인 만큼 알려진 사람도 없을 것이다. 그는 과학의 영역을 넘어서서 우리들 생활과 철학에 큰 영향을 준 몇사람 되지 않은 과학자의 대표주자이기도 하다.

수많은 화제를 남긴 이 천재는 오늘날 과학의 핵심을 차지하고 있는 양자론(Quantum Theory)에 대해서도 많은 화제를 뿌렸다. "신이 주사위 놀이를 할 리가 없다"는 유명한 말로 양자론의 기본개념에 대한 강한 회의와 불만을 토로한 것이다. 아마 아인슈타인은 죽을 때까지 양자론에 마음 속에서 충심으로 승복하지는 않았던 것 같다.

그렇지만 그는 양자론이 등장하는데 빼놓을 수 없는 중요한 노릇을 했다. 전자의 법칙이 맥스웰방정식이라는 형태로 완성된 19세기가 끝나가면서 빛은 전기와 자기의 파동인 것이 명백해진다. 빛은 회절을 하고 간섭무늬를 만들기에 파동임이 틀림없다고 모두가 믿고 있었다.

아인슈타인은 입자파

그 옛날 뉴턴은 빛이란 입자이기 때문에 자신이 만든 뉴턴의 법칙에 따라 아무런 힘을 받지 않는 공간에서는 직진하며, 물체 뒤에 그늘이 생기는 것은 직진하는 입자가 물체에 걸려서 가지 못하는 데서 일어나는 현상이라고 했다. 두 입자는 같은 시간에 같은 장소를 차지할 수 없는 반면 파동은 중첩이 가능하다. 가령 두개의 당구공은 동시에 한 자리를 차지하지 못 하고 부닥쳐서 튕겨나겠지만 파동인 물결은 입자와는 다른 성질을 갖는다. 파동의 산과 골이 만나면 파동은 없어지고 산과 산이 만나면 파동은 두배로 높아지게 된다. 반면에 두개의 당구공이 합쳐져 없어졌다는 말을 들어 본 사람도 없거니와 당구공이 합쳐져서 갑자기 그 크기가 두배가 되었다는 말 역시 들어본 적이 없을 것이다. 이와 같이 파동과 입자는 판이한데 아인슈타인은 빛이 입자라고 주장한 것이다.

아인슈타인은 광전효과라는 현상을 설명하면서 빛은 입자의 성질을 가져야만 된다고 주장했다. 광전효과란 금속면에 빛을 쪼이면 전자가 튀어나오는 현상을 말한다. 실험에 따르면 같은 색깔, 즉 같은 진동수의 빛을 쪼이면 튀어나오는 전자 하나하나의 에너지는 일정하고 같은 진동수지만(같은 파장이지만) 더 강한 빛을 쪼이면 더 많은 전자가 튀어나올 뿐 개개 전자의 에너지는 변함이 없다는 것이 알려져 있었다.

'광전효과'라고 알려진 이러한 현상은 파동으로 설명하기는 곤란하다. 파동의 강도는 파동의 진폭, 즉 파동의 높이의 자승에 비례한다는 것은 잘 알려진 사실이다. 빛이 파동이라면 강한 빛이란 진폭이 큰 파동을 말하므로 금속 속의 전자 역시 많이 흔들릴 것이고 이 전자가 금속표면을 벗어날 때는 역시 많은 에너지를 갖고 나을 것이다. 즉 나오는 전자 하나하나의 에너지는 빛의 강약에 따라 많고 적어진다는 것이다. 그렇지만 실험사실은 튀어나오는 전자의 에너지는 빛의 진동수, 즉 색깔에만 관계되지 빛의 강약에는 무관하다는 것이다.

양자론의 성립에 기여

아인슈타인은 플랑크(Max Planck) 상수 h와 빛의 에너지 E는 E=hv로 되고(여기서 v는 빛의 진동수) 운동량(속도와 질량을 곱한량에 해당하는데 상대론에서는 이 운동량 자체가 속도보다 더 근본적인 양으로서 운동량 P와 에너지 E로서 4차원 벡터를 이루고 있다. 이해가 가지 않으면 괄호속의 글은 무시하기 바란다) P와 플랑크 상수 h는 드브로이의 관계식 P=hv/c (여기서 c는 빛의 속도)로 표현된다는 양자론을 받아들이면 광전 효과가 설명된다는 것을 보여주었다.

즉 hv의 에너지를 갖는 빛의 알갱이인 광량자가 금속 속의 전자와 충동하여 그 에너지를 전자에게 넘겨줌으로써 진동수 v(또는 그의 역수인 파장)가 같으면 같은 에너지를 갖는 전자가 튀어나올 것이 예상된다. 빛이 강하다는 것은 (빛이 입자라고 할 때) 광량자가 많다는 것에 해당되므로 당연히 충돌하는 횟수가 잦아서 금속표면에서 튀어나오는 전자도 많다는 것이 된다고 설명했다.

그렇지만 엄연히 빛은 간섭과 회절현상이 보이므로 파동임에 틀림없다. 이렇듯 빛은 입자와 파동이란 서로 상반된 양면을 지니고 있다. 이는 양자론의 기본 개념인 이중성으로서 모든 소립자에 적용된다.

이렇듯 아인슈타인은 양자론의 기본개념을 정립한 사람 중의 하나이고 광전효과의 공로로 노벨물리학상을 받은 것도 널리 알려진 사실이다.
"같은 대상물이 파동인 동시에 입자이기도 하다"는 이중성의 본보기에서 나타나듯 양자론의 개념은 상식과는 거리가 멀다. 실상 양자론에서는 전자 역시 파동인 동시에 입자이고, 또한 여기와 저기에 동시에 있을 수 있다고 한다.

여기와 저기에 동시에 있으면서 파동처럼 보이지만 막상 그 위치를 관측하면 입자인 것이 틀림없다. 양자론에서는 여기에 있을 확률이 20%, 저기에 있을 확률이 80%라는 표현을 쓴다.

원자 속의 전자는 여기에 있을 수 있고 저기에 있을 수도 있으며, 다만 여기에 있을 수 있는 확률이 몇%, 저기에 있을 수 있는 확률이 몇%인 것 이외에는 더 상세하고 확실한 것을 알 수 없다는 것이 양자론의 기본 개념이기도 하다. 마치 주사위 놀이를 할 때 1이 나타날 확률이 1/6이지만 막상 주사위를 던지고 나면 1에서 6까지 숫자중 어느 숫자 하나가 나타나는 것처럼 전자 역시 그 위치를 확인하면 마찬가지 결과가 나타난다.

아인슈타인은 이런 확률적인 존재를 좋아 하지 않았고 이를 "하느님이 주사위 놀이를 좋아할 리가 없다"고 표현한 것이다. 그렇지만 주사위놀이는 아인슈타인 자신이 내세운 광전효과의 설명 속에 들어 있었고 좋든 나쁘든 자기 자신이 주사위놀이를 만들어낸 사람이기도 하다.

유령의 원격작용

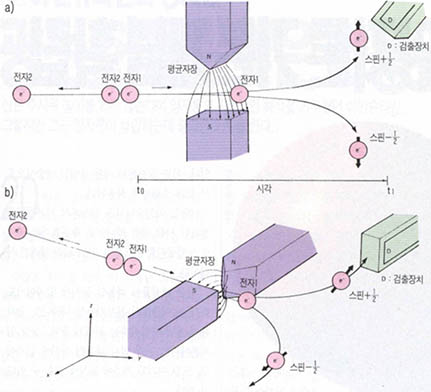
아인슈타인은 물리적으로 관측하는 것이 그 상태를 결정짓는다는 양자론의 개념에도 반감을 갖고 있었다. 아인슈타인―포돌스키―로젠 파라독스를 발표함으로써 이를 정면으로 반박했다. 양자론에 따르면 어떤 현상을 실제로 관측하기 전에는 그 상태 자체가 무엇인지 알 수 없다는 것이다.

예를 들어 정지해 있는 원자핵에서 두개의 중성자가 튀어 나왔다고 하자. 우리들이 그중 한 중성자의 운동방향을 관측하기 전에는 중성자는 어떤 방향이든 모든 방향으로 움직이는 것이 가능하고 일정한 방향으로 나오는 것은 다만 확률로서 주어질 따름이다. 그렇지만 그중 하나의 운동방향을 관측하면 다른 중성자의 방향도 완전히 결정된다는 것이다. 비록 그 다른 중성자는 벌써 은하계의 저쪽을 넘어섰을 정도로 멀리 있다 하여도 그 성질이 이쪽에 있는 중성자를 관측함으로써 결정된다는 것이다. 아인슈타인은 이를 유령의 원격작용(spooky action at a distance)이라 이름짓고 그럴 수 없다고 주장하고 나섰다. 이것이 바로 아인슈타인―포돌스키―로젠(EPR) 파라독스인 것이다.

아인슈타인의 생각에는 저 멀리 떨어져 있는 대상물의 상태가 이곳의 대상물을 관측함으로써 결정된다는 것이 못마땅했던 것이다. 관측을 해야만 상태가 결정된다는 것을 비꼬는 말 가운데 "우리들이 달을 보고 있지 않을 때 달은 과연 거기에 있을까?"라고 말하고 있다.

그러나 1964년에 한쪽 중성자의 운동방향(사실은 스핀이란 각운동량이었지만)을 측정하면 다른 쪽도 결정된다는 '벨의 부등식'이 등장했다. 프랑스 태생 물리학자인 에리언 아스페크는 실험에 의해 '벨의 부등식'을 검증함으로써 전통적인 양지론이 옳다는 것을 증명하기에 이른다.
양자론적인 세계관에서는 파동의 중첩(superposition)이 가능하듯 시물의 상태 역시 중첩된 상태로 있다.

상대론과 우주론의 대가이며 항상 멋있는 말을 하는 존 휘러의 말을 빌리면 "양자론적 상태는 연기로 된 용처럼 정체를 잡기가 어렵다"고 한다. 극단적인 예를 들면 골목길에서 나오는 동물을 확인하였더니 개였지만 또 다시 돌아보니 고양이였다는 것이다. 그 동물은 고양이와 개로서 구성되어 있지만 우리들이 그 정체를 볼 때는 고양이거나 개이지 이것도 되고 저것도 되는 것은 아니다. 관측했을 때는 고양이거나 개이지 중간상태는 절대 없지만 관측을 하지 않았을 때는 개와 고양이가 반반 섞인'개양'이라는 것이 양자론적인 입장이다.

아인슈타인은 이러한 해석을 좋아하지 않았다. "우리가 보지 않고 있을 때 과연 달은 거기에 있을까?" 여운을 남기는 말이기도 하다.