d라이브러리

지구 중력장만을 고려한다면 가장 멀리 던지는 방법은 45°다. 하지만 공기저항에 의한 마찰력이 있기 때문에 실제는 이와는 다른 결과가 나타난다.

떨어지는 낙엽, 야구공과 총알의 운동, 로켓의 운동까지 우리 주변에서 움직이는 모든 물체는 중력의 영향을 받는다.

중력장에서 물체 운동을 분석하는 데 있어서 기본이 되는 것은 자유낙하운동이므로 먼저 자유낙하운동에 대해 알아 본 다음 포물선운동과 '원숭이와 사냥꾼 문제'를 컴퓨터를 이용한 모의실험을 통해 화면에 나타내 보자.

무거울수록 빨리 떨어질까?

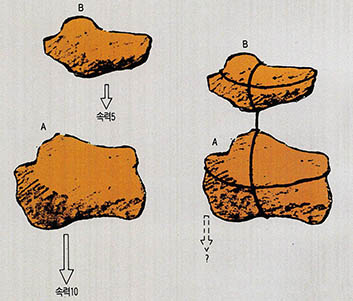
갈릴레이는 아리스토텔레스가 주장한 '무거운 물체일수록 빨리 떨어진다'는 학설을 비판하면서 다음과 같은 사고실험(思考實驗)을 제시했다.

"지금 무거운 돌 A와 가벼운 돌 B가 자유낙하하고 있다고 하자. 아리스토텔레스 학설이 옳다면 A가 B 보다 먼저 떨어질 것이다. 이제 두 돌을 하나로 묶어 낙하시키면 더 무거워졌으므로 A보다 더 빨리 떨어져야 한다.

그러나 가벼운 돌 B는 A보다 늦게 떨어져야 하므로 A를 뒤로 당겨, 묶어 놓기 전보다 A는 더 늦게 떨어져야 한다.

위 두 해석이 상호 모순이 되기 때문에 무거울수록 빨리 떨어진다는 전제는 잘못된 것이다."(그림1)

지구가 당기는 힘은 물체의 질량에 비례하지만 가속도의 크기는 질량에 반비례하므로 질량으로 인한 효과는 상쇄된다. 그래서 모든 물체의 가속도는 같게 되며, 이 값을 중력가속도라고 하고 약 9.8m/${s}^{2}$이다.

어떤 물체든지 자유낙하 1초 후에는 속력이 9.8m/${s}^{2}$ 이며 2초 후에서 19.6, 3초 후에는 29.4,…해서 t초 후에는 9.8t 가 된다.

또 1초동안 낙하한 거리는 1초동안의 평균속도 4.9x1=4.9 이고 2초 동안의 낙하거리는 평균속도 9.8x2=19.6, 3초에는 14.7x3=44.1 … 해서 t초 후에는 평균속도 4.9t x t=4.9${t}^{2}$ 이다. 다리 위에서 떨어뜨린 돌이 2초만에 물에 들어 갔다면 다리의 높이는 19.6m 라고 할 수 있다. 물론 이같은 계산은 공기의 저항을 무시했을 경우이다.

실제로는 공기의 저항 때문에 자유낙하하는 물체의 속력이 무한정으로 증가하지는 않는다. 빗방울의 운동이 그것인데 만약에 공기의 저항에 의해서 속도가 제어 되지 않는다면 빗방울이 총알처럼 우리 머리에 떨어져 소나기에 맞아 죽는 사태가 발생할지도 모른다.

공기에 의한 마찰력은 속력에 따라 증가하며 무거운 물체는 속력의 제곱에, 가벼운 물체는 속력에 비례하여 마찰력이 커진다고 한다.

처음에는 물체에 작용하는 중력이 마찰력보다 커서 아래로 가속되지만 속력이 증가함에 따라 마찰력도 점점 커져서 중력과 같아지면 그 물체에 작용하는 알짜의 힘은 0이 된다. 그때부터 물체는 등속으로 움직이게 되는데 이를 '종단속도'라 한다. 빗방울은 땅에 떨어지기 훨씬 전에 종단속도에 도달된다. 속도의 제곱에 비례하는 힘이 작용하는 경우, 빗방울의 운동이 어떻게 될지를 컴퓨터를 이용해서 계산해 보기로 하자.

질량이 m인 물체에 작용하는 중력은 ㎎, 마찰력은 ${cv}^{2}$이므로 그 물체에 작용하는 알짜의 힘은 ㎎—${cv}^{2}$ 이다. 따라서 물체의 가속도는 g-${kv}^{2}$이 되며 k=c/m 이다.

알짜의 힘이 속력에 따라 변하므로 시간을 조금씩 증가시켜 가면서 그때 그때의 속력과 가속도를 계산한다. 계산 횟수가 많지만 계산하는 방식이 항상 일정하므로 컴퓨터로 프로그램화하면 효율적으로 계산할 수 있다. 프로그램 언어는 가장 보편적으로 쓸 수 있는 BASIC을 이용해 만들었다(프로그램1).

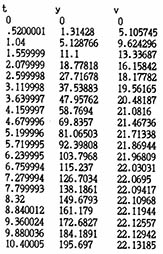
DT는 계산하는 시간 간격이고 TI는 프린트 하는 시간 간격이다. TM이 될 때까지 계산을 계속하도록 한다. K=0.02, DT=0.02, TI=0.5, TM=10 일때의 결과를 보면 10초가 지날 때 속력이 22.13으로 거의 일정하며 그 동안 이동거리가 1백90m임을 알수 있다. 마찰이 없었다면 지유낙하 10초후에 속도는 98m/s이며 낙하거리는 4백90m이다.

가장 멀리 던지는 방법

체력검사 종목중에 멀리던지기가 있다. 공을 멀리 던질수록 높은 점수를 받게 되는 검사다. 세게 던질수록 멀리 나가는 것은 당연하지만 던지는 각도와도 관계가 있다.

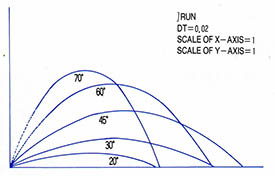
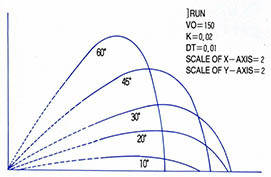
중력장에서 공을 비스듬히 던졌을 경우 수평방향으로는 등속직선운동을 하고 수직방향으로는 등가속도 운동을 한다. 그 두가지 운동이 독립적으로 합성되면 포물선을 그리게 되는데 약간의 수학을 동원하면 45°로 던졌을 경우에 가장 멀리 나간다는 것을 증명할 수 있다. 그 때 물체가 지나게 되는 경로를 계산해서 모니터에 표시하는 프로그램이 (프로그램2)다. 역시 45° 일때 가장 멀리 나가며, 20도와 70도, 30도와 60도에서 같은 곳에 떨어진다는 것을 보여 준다.

그러나 2차대전 때 독일군이 파리 시내를 장거리포를 사용하여 폭격한 기록에 따르면 45°보다 52°로 포격 할 때 수배나 멀리 나갔다고 한다. 이는 올라갈수록 공기의 마찰이 급격히 줄어드는 것과 상공에 존재하는 기류을 타서 그렇게 된 것이라 해석할 수 있다.

한편 올림픽의 던지기 종목에서 금메달을 받은 선수들이 던지는 각도는 40°가 못된다는 분석이 나와 있다. 공기의 저항 때문인데, 속력의 제곱에 비례하는 마찰력이 작용한다고 가정하면 수평방향은 마찰력만이 작용하고 Fx= -Cvvx, 수직방향의 힘은 중력에 마찰력을 빼야 하므로 Fy=-mg-Cvvy다. 따라서 수평방향의 가속도 ax=-Kvvx, 수직방향의 가속도 ay=-g-Kvvy 이다. 속도와 가속도가 시시각각 변하므로 시간을 조금씩 증가시켜가면서 컴퓨터로 궤도를 추적해 갈 수 있다.

던지는 각도는 10, 15, 20, 30, 45, 60, 70, 80°로 하여 계산 결과를 컴퓨터 화면에 점을 찍어 가면 궤도를 그릴 수 있다(프로그램3).

사냥꾼과 원숭이 문제

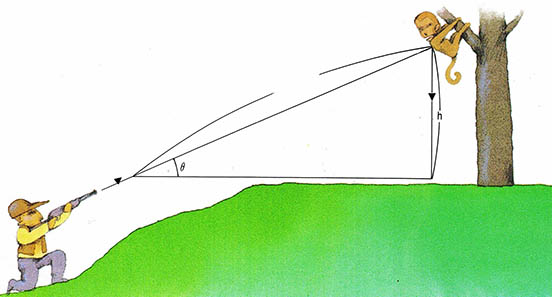
원숭이를 죽이느냐 살리느냐 하는 문제는 덮어 두고 우리는 순전히 역학적인 관점에서만 이 문제를 취급하기로 한다. 전통적으로 물리교과서에 자주 인용되는 문제중의 하나로 다음과 같은 문제가 있다.

"지상 h 높이의 나무 위에 있는 원숭이를 사냥꾼이 지면과 θ의 각도로 원숭이를 겨냥하고 초속 vO로 탄환을 발사했다. 원숭이는 탄환이 발사되는 순간 재빨리 나무에서 손을 놓고 지상으로 자유낙하를 시작했다. 과연 이 원숭이는 살아날 수 있을까?"

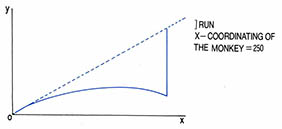
대답은 원숭이의 재빠른 행동에도 불구하고 총알이 원래 겨냥하던 곳에 정확히 맞는다는 것이다. 중력이 작용하지 않는다면 원숭이가 손을 놓아도 제자리에 있을 것이므로 당연히 맞을 것이고, 중력이 작용하여 원숭이가 자유낙하하면 총알도 역시 같은 중력을 받아 궤도가 포물선를 그리게 되는데 원래의 궤도에서 아래로 이탈된 정도는 그 사이에 자유낙하한 거리와 같다. 따라서 총알과 원숭이는 어느 하나가 먼저 땅에 떨어지지 않는한 총알의 속도에 관계없이 반드시 만나야 한다.

사냥꾼이 30°의 각도로 원숭이를 겨냥하고 총을 쏜 경우, 총과 원숭이의 거리를 달리했을 때 총알과 원숭이가 어떤 방식으로 만나는 지를 (프로그램4)로 확인할 수 있다.