d라이브러리

영국의 과학자들은 최근 새로운 완전수와 솟수를 발견해냈다. 이 작업에는 슈퍼컴퓨터까지 가담했는데….

풀어보고

(1) 다음 문제는 주변을 돌아보지 말고 기억만으로 답해보기 바란다. 다음 그림은 두가지로 표시된 숫자판의 일부이다. 계산기와 전화기의 번호판은 각각 어떤 형태로 되어 있을까?

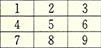
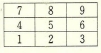
① 가, 가 ② 나, 나 ③ 가, 나 ④ 나, 가

(2) 어떤 삼각형의 세 변의 길이가 연속되는 정수로(물론 0이 아니므로 자연수)되어 있다. 그리고 가장 큰 내각이 가장 작은 내각의 2배이다. 이때 이 가장 작은 내각의 코사인(cos) 값은 얼마일까?
① $\frac{3}{4}$ ② $\frac{7}{10}$ ③ $\frac{2}{3}$ ④ $\frac{9}{14}$

(3) 한 물체가 z=$\frac{h}{2}$와 z=$\frac{h}{2}$로 표시되는 두 평면에 의해 정해져 있다. 여기서 z는 물체의 축 방향좌표이다. 또 이 사이의 면들은 다음 식으로 면적(A)이 주어져 있다.
A=${a}_{0}$${z}^{3}$+${a}_{1}$${z}^{2}$+${a}_{2}$z+${a}_{3}$ 여기서 ${a}_{0}$, ${a}_{1}$, ${a}_{2}$, ${a}_{3}$는 상수이며 0일 수도 있다. 이때 이 물체의 체적은 다음 식중 어느식으로 표시될까? 다음 식에서 ${B}_{1}$, ${B}_{2}$는 z=$\frac{h}{2}$, z=-$\frac{h}{2}$로 표시되는 물체 끝면의 면적, M은 z=0으로 표시되는 물체 중간면의 면적이다. ${a}_{0}$가 0이면 우리가 잘 아는 원추나 구의 경우가 된다.
① $\frac{1}{3}$h[${B}_{1}$-${B}_{2}$+M]
② $\frac{1}{6}$h[${B}_{1}$+${B}_{2}$+M]
③ $\frac{1}{6}$h[${B}_{1}$+${B}_{2}$+4M]
④ $\frac{1}{3}$h[${B}_{1}$-${B}_{2}$+4M]

(4) 1과 자신 외에는 나누어지는 수가 없는 숫자를 솟수라 하고, 6=1+2+3 처럼 자기 자신과 인수의 합이 같은 수를 완전수라고 한다. 최근 영국에서는 현재까지 가장 큰 솟수인 22만7천8백32자리의 숫자와 45만5천6백63자리수의 완전수를 발견했다고 한다. 이 완전수는 몇번째의 완전수일까?
① 10 ② 32 ③ 99 ④ 500

맞춰보고

(1) ④일반적으로 계산기와 전화기의 번호판은 다음과 같다.
 

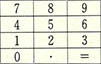
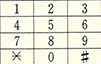
컴퓨터의 자판중 오른쪽에 따로 나와 있는 숫자판은 다음과 같다.
 

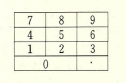
평소에 주의를 기울이지 않았던 독자들은 어느 쪽이 어느 쪽인지 기억해내기 어려웠을 지도 모른다. 이 문제는 단순히 여러분의 기억력 또는 평소의 주의력을 테스트하고자 하는 것보다 훨씬 큰 의미를 담고 있다.

다 같이 숫자를 주로 사용하는 자판인데 왜 이렇게 달라졌을까. 끔씩 이 자판을 사용하는 경우에는 별 문제가 없어도 전문적으로 자료를 입력하는 경우에는 시간이나 입력시의 노동에 큰 차이를 줄 수 있을 것이다. 이 이유에 대해 여러 가설이 있다. 그중 하나는 계산기를 사용하면서 이미 빠른 속도로 자판을 찍을 수 있게 된 사람들이 천천히 전화기의 자판을 누르도록 유도하기 위해서라는 가설이다. 전화기로 신호를 보내는데 무리가 없도록 하기 위하여 전화회사에서 일부러 그렇게 했다는 것이다. 전기의 속도를 생각해 보면 이 설은 물론 옳은 이야기가 아니다.

전화기 자판과 전체가 트랜지스터로 된 계산기는 1960년대 초반부터 선보이기 시작 했다. 전화기와 계산기는 시작부터 1, 2, 3 을 각각 상단과 하단에 배치하고 있었다. 이 자판들은 각각 만들어질 당시의 상황을 따랐다는 것이 일반적으로 받아들여지고 있는 설이다. 후에 나온 전자식 계산기의 자판은 그 전에 사용하던 현금출납기를 따르게 되었다. 이 현금출납기들은 맨 왼쪽 줄에 위에서부터 아래로 9에서 0까지 배열되어 있었다. 그 옆줄은 90에서부터 10까지, 그 다음 줄은 900에서 100까지 순으로 되어 있었다. 실제로는 못본 독자들도 있을 것이나 서양영화에서는 가끔 볼 수 있다. 이를 따라 계산기는 7-8-9를 맨 윗줄에 왼쪽에서 오른쪽으로 배치했던 것이다. 이와 유사하게 전화기판도 지금은 거의 볼 수 없지만 오랫동안 쓰였던 회전 다이얼식 전화기로부터 영향을 받은 것이다.

회전다이얼식은 가까운 위치에서부터 1, 2, … 9, 0으로 배열돼 있다. 지금은 톤(tone) 방식 사용으로 번호간에 차이가 없어졌지만 회전 다이알식전화기를 사용할 때 0000번 등은 걸기 어려운 번호였던 것이다. 112 등 11*으로 나가는 번호가 중요한 번호로 채택된 이유도 이런 배치와 무관하지 않다. 따라서 1을 맨 앞에, 7-8-9-0을 맨 아래 배치하게 된 것이다. 또 인간공학적 연구에 의하면 이 배열이 전화거는데 실수할 확률이 가장 적다는 것이다. 초창기의 전화회사에 따르면 당시 계산기 제조의 선두주자였던 샤프사(Sharp)나 텍사스 인스트루먼트사 (Texas Instruments)에서는 이런 연구가 없었다고 한다. 이 이야기는 많은 공학적 설계가 전통이나 관성에 의해 얼마만큼 영향을 크게 받나 하는 것을 보여주는 좋은 예다.

이 자판문제는 매우 중요해서 큰 이슈가 되어 있다. 미국에서는 오랫동안 써오던 쿼티(QWERTY)자판(맨 윗줄에 왼쪽부터 qwerty…둘째줄에 asdf…으로 배열된 자판)을 버리고, 연구결과 훨씬 우수하다고 결론이 난 드보락(Dvorak)자판으로 바꾸는 운동을 벌이고 있다. 한국에서는 컴퓨터 내부의 한글처리 문제와 맞물려 있다. 즉 완성형이냐 조합형이냐의 문제와 연결되어 2벌식 3벌식 자판에 대한 선택이 논란이 되고 있다. 과학적이고 합리적인 자판으로 빨리 결정되어야 나중에 혼란을 감소시킬 수 있을 것이다.

이와같은 맥락에서 다음과 같은 물음을 던질 수도 있다. 왜 시계는 시계방향으로 도나. 여기서 "시계가 도는 방향을 시계방향이라 부른 거지"하면 과학적인 답이 못된다. 마당히 왜 그 방향이어야 하는가를 밝히는 답이어야 한다. 이에 대한 답은, 자판문제와 같이, 기계적 시계가 발명되었을 때 시계의 숫자판과 시계바늘의 도는 방향은 그 이전에 사용했던 해시계를 본 따 해의 그림자가 도는 방향으로 정했기 때문이다.

(2) ①세 변의 길이를 n-1, n, n+1 이라고 하면 이 삼각형은 다음의 형태가 될 것이다.

삼각형의 사인(sine)공식에 의하면 $\frac{sinθ}{n-1}$=$\frac{sin(2θ)}{n+1}$=$\frac{2sinθ cosθ}{n+1}$ 즉 cosθ=$\frac{n+1}{2(n-1)}$ 또 삼각형의 코사인(cos)공식에 의하면 cosθ=$\frac{n²+(n+1)²-(n-1)²}{2n(n-1)}$ 윗 식에서 cosθ=$\frac{n+1}{2(n-1)}$ 이식을 풀면 n=5 따라서 cosθ=$\frac{5+1}{2(5-1)}$=$\frac{3}{4}$

(3) ③문제가 좀 어려웠을지 모르겠으나 이 문제는 미국의 유명한 풋남(Putnam) 대학생 수학 경시대회의 1938년 제1회 대회, 1번 문제이다.
문제에서 체적(V)은 정의에 따라 다음과 같이 구해진다.
V=${∫}_{-h/2}^{h/2}$ (${a}_{0}$${z}^{3}$+($a_0z³+a₁z²+a_2z$+a₃)dz=$\frac{{a}_{1}}{12}$${h}^{3}$+${a}_{3}$h z=h/2, -h/2의 면적은 각각${B}_{1}$=$\frac{{a}_{0}{h}^{3}}{8}$+$\frac{{a}_{1}{h}^{2}}{4}$+$\frac{{a}_{2}h}{2}$+${a}_{3}$${B}_{2}$=-$\frac{{a}_{0}{h}^{3}}{8}$+$\frac{{a}_{1}{h}^{2}}{4}$-$\frac{{a}_{2}h}{2}$+${a}_{3}$ M=+${a}_{3}$가 된다. 따라서 V=$\frac{{a}_{1}{h}^{3}}{12}$+${a}_{3}$h=$\frac{1}{6}$h($\frac{{a}_{1}{h}^{2}}{2}$+6${a}_{3}$)=$\frac{1}{6}$h[${B}_{1}$+${B}_{2}$+4M]
만약 물체가 원추라면 B1=B, B2=0, M=B/4가 되어 잘 아는 원추의 체적공식 V=Bh/3이 된다. 또 물체가 반지름 r의 구라면 A=π(${r}^{2}$-${Z}^{2}$)이 되고 ${B}_{1}$=${B}_{2}$=0, M=π${r}^{2}$이 되어 체적 V는 다음과 같이 된다.
V=$\frac{4}{6}$4π${r}^{2}$=$\frac{4}{3}$4π${r}^{2}$ 체적의 기본원리와 적분의 기본을 알고 있으면 어렵지 않을 것이다.

(4) ②최근의 발표에 따르면 영국의 과학자들은 새로운 솟수와 완전수를 발견했다고 한다. 이 솟수는 ${2}^{756839}$-1이다. 지난 85년에 발견된 ${22}^{216091}$-1 의 65050자리수보다 162782자리수가 많은 큰 수이다. 또 32번째의 완전수는 새로 발견된 솟수에 ${2}^{756838}$을 곱한 수이다. 이 솟수는 데르센느수라고 불리는 수인데, 프랑스의 성직자인 메르센느(Marin Mersenne, 1588~1648)의 이름을 딴 것이다. 이 메르센느는 ${2}^{n}$-1의 꼴의 솟수와 완전수와의 관계를 연구하였다. 즉 n이 솟수일 때 ${2}^{n}$-1의 꼴의 숫자가 메르센느수이다. 또 이에 해당하는 완전수는 (${2}^{n-1}$x(${2}^{n}$-1)이라는 것이다.

이 솟수의 개수는 무한하다는 것이 알려져 있는데 실제로 찾아내는 일은 매우 어려운 일이다. 최근의 발견에는 슈퍼컴퓨터가 사용되었고, 이 과학자들은 앞으로 현재의 슈퍼 컴퓨터 보다 훨씬 강력한 슈퍼컴이 등장하지 않는 한 더 큰 솟수나 완전수를 발견해내기는 어려울 것이라 전망하고 있으니 말이다. 완전수를 몇개 들어 보면 6, 28, 496, 8128, 33550376, …등이다.