d라이브러리

중력가속도를 이용해 지구의 질량을 계산해보고 인공위성이 지구궤도 위를 도는 원리를 알아본다.

지난 6월호에서 공부한 내용을 간단히 복습해 보자.

힘을 F, 질량을 m, 가속도를 a라 하면 뉴턴의 운동법칙은 방정식 F=ma (1)로 주어진다.

뉴턴의 만유인력법칙에 따르면 질량이 각각 ${m}_{1}$, ${m}_{2}$인 두 물체가 거리 r만큼 떨어져 있으면 그 사이에는 F=${m}_{1}$${m}_{2}$/${r}^{2}$ (2)인 만유인력이 작용한다.

이것을 바탕으로 해 중력가속도의 응용이랄 수 있는 지구 질량 측정에 관해 알아보자.

중력도 힘이므로 그것에 상응하는 가속도가 있다. 물체를 자유낙하시키면 물체는 밑의 방향으로 점점 더 빨라지게 되는데 이는 바로 가속도가 존재한다는 증거이다. 그 가속도를 바로 중력가속도라고 부르고 g로 나타낸다. g의 크기는 누구나 일상 경험을 통하여 잘 알고 있는데, 바로 그 가속도의 크기가 우리가 과학 시간에 말하는 g=980cm/${초}^{2}$다.

엄밀하게 말한다면 뉴턴의 만유인력에 의한 힘이 중력과 똑같은 것은 아니다. 예를 들어 같은 지구 표면상이라도 지구의 자전에 따른 원심력의 크기가 위치에 따라 다르므로 중력가속도 역시 달라진다. 하지만 이 글에서는 중력가속도가 지구 표면에서는 어디에선 g=980cm/${초}^{2}$으로 같다고 가정한다.

따라서 물체의 무게 W는 식(1)에 의해 W=mg (4)로 주어진다. 그런데 이것은 바로 식(3)과 같아야 하므로 우리는 mg= GMm/${R}^{2}$를 얻는다. 양변에서 m을 소거하고 정돈하면 M=g${R}^{2}$/G (5)와 같이 지구의 질량을 구할 수 있다.

실제로 식 (5)에 측정값들인 R=6.3×${10}^{8}$cm와 G=6.67×${10}^{-8}$ CGS를 대입하면 지구 질량은 M=980x${(6.3×{10}^{8}}) ^{2}$÷6.67×${10}^{-8}$≒6×${10}^{27}$g이 된다.

케플러의 천재성
 

17세기 초 케플러( kepler )는 브라헤(Brahe)의 육안 관측 자료를 정밀하게 분석한 후 다음과 같은 세가지 행성운동의 법칙을 발표했다.

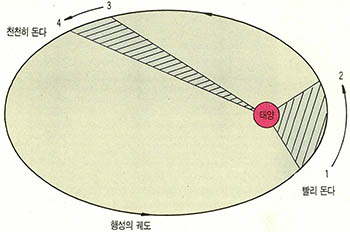
1. 타원 궤도의 법칙 : 행성은 태양 주위를 타원을 그리며 공전하고 있다. 타원에는 2개의 초점이 있는데 태양은 이 중 어느 하나에 위치한다.

2. 면적 속도 일정의 법칙 : 행정은 태양에 가까울 때 빨리 공전하고 멀 때 느리게 공전한다. 그리하여 행성과 태양을 이은 직선이 같은 시간 동안 휩쓰는 면적은 언제나 일정하다.

3. 조화의 법칙 : 행성 궤도의 장반경을 a, 공전 주기를 P라 하면 모든 행성에 대하여 ${P}^{2}$을 ${a}^{3}$으로 나눈 값은 일정하다.

${P}^{2}$/${a}^{3}$=상수 (6)

첫번째 법칙은 천문학사에서 매우 중요한 의미를 갖는다. 왜냐하면 당시의 모든 사람들은 행성이 원 궤도를 그린다고 믿고 있었기 때문이었다. 원은 옛날부터 '완전한 도형'으로서의 이미지를 지니고 있었다. 그러한 원 궤도의 '신앙'을 혼자서 과감히 부정하고 타원 궤도의 이론을 주장하는 데에서 케플러의 천재성이 발휘되기 시작한다. 어쩌면 세 법칙 중 가장 값어치가 있는 것인지도 모른다.

두번째 법칙은 (그림 1)에서 쉽게 이해될 줄로 믿는다. 독자가 직접 손가락으로 (그림1)의 궤도에서 행성의 공전을 흉내내 보면, 즉 태양 가까이에서는 손가락을 빨리 움직이고 멀리에서는 손가락을 천천히 움직여 보면 더 이해가 쉬워진다. 행성의 궤도상에서 태양에 가장 가까운 점을 근일점, 태양에 가장 먼 점을 원일점이라고 한다. 따라서 행성은 근일점에서 가장 빨리 운동하고 원일점에서 가장 느리게 운동한다.

세번째 법칙을 이해하기 위해서 공식을 직접 유도해 보기로 한다. 타원운동의 경우 케플러 법칙을 유도하는 것은 대학 전공 과정에서나 가능하므로 여기서는 원운동을 하는 행성의 경우에 국한해 살펴보자.

먼저 등속원운동에 관해 알아보기로 하자. 질량 m인 물체가 일정한 속력 v로 반지름이 r인 원운동을 하고 있는 경우 작용하는 원심력 F는 F=m${v}^{2}$/r (7)로 주어진다. 여기서 v는 속도가 아님에 유의하자. 즉 등속원운동이란 '등속도 원운동'이 아니라는 뜻이다. 이에 대한 자세한 설명은 벡터라는 수학을 이용해야만이 가능한데 이 글에서는 생략하기로 한다.

식 (7)에서 알 수 있듯이 질량이 2배 3배… 커지면 원심력은 비례하여 2배 3배… 커지고, 속력이 2배 3배 …커지면 원심력은 제곱이 비례하여 4배 9배… 커진다. 또한 반지름이 2배 3배… 커지면 원심력은 반비례하여 2배 3배… 작아진다.
 

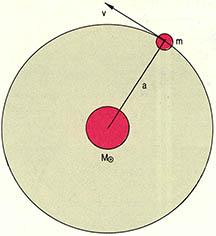
행성이 등속원운동을 하며 안정된 궤도상에서 태양을 공전하는 경우 태양이 잡아당기는 구심력과 방금 알아 본 원심력은 서로 크기가 같아야 한다. 만일 구심력이 크면 행성은 태양쪽으로 더 가까워져야 하고, 원심력이 크면 행성은 태양으로부터 더욱 멀어져서 안정된 궤도를 이루지 못하게 된다. 따라서 (그림 2)에서 처럼 태양의 질량을 ${M}_{⊙}$, 행성의 질량을m, 행성의 속력을v, 행성 궤도의 반지름을 a라고 하면 식 (2), 식 (7)로부터 G${M}_{⊙}$m/${a}^{2}$=m${v}^{2}$/a를 얻고 이 식을 정돈하면 ${v}^{2}$=G${M}_{⊙}$/a (8)가 된다.

행성의 공전 주기를 P라 하면 v는 공전궤도의 총길이 2πa를 P로 나눈 값이 되어야 하므로 식 (8)은 ${(2πa/P)}^{2}$=G${M}_{⊙}$/a가 되고 정돈하면 ${M}_{⊙}$${P}^{2}$=(4${π}^{2}$/G)${a}^{3}$, (9) 즉 케플러 법칙을 얻게 된다.

그런데 식 (9)에서 만일 우리가 ${M}_{⊙}$=1로 놓고 P의 단위로 년, a의 단위로 AU(Astronomical Unit, 천문 단위 : 지구 공전 궤도의 평균 반지름)를 사용하면 식 (9)는 단순히 ${P}^{2}$=${a}^{3}$ (10)이 된다. 즉 식 (6)의 상수는 마술처럼 1이 되는 것이다. 지구의 경우 P=1, a=1이므로 이는 쉽게 확인된다. 또 예를 들면 목성의 경우 P=11.86, a=5.20이므로 식 (10)의 양변은140.6 정도로 같아진다. 식 (9)가 우리 태양계의 경우 식 (10)처럼 간단해지는 것은 물론 단위들이 그렇게 정의되었기 때문이다.

지구가 현재의 공전 궤도를 유지하고 있는 상태에서 그럴리는 없지만 갑자기 태양의 질량이 4배로 불어났다고 하자. 그랬을 때 지구의 공전 주기에는 어떠한 변화가 일어나는지 생각해 보자. 태양의 질량이 갑자기 늘어났다는 말은 태양의 중력이 더욱 강해졌다는 이야기이다. 이렇게 구심력이 더욱 강해진 상태에서 지구가 종전 궤도를 유지하는 길은 더욱 빨리 공전하여 원심력을 증가시켜서 대항하는 수밖에 없다. 즉 지구의 공전 주기는 짧아져야 한다. 그럼 얼마나 짧아져야 할까. 이는 식 (9)를 제대로 이해한 사람이면 암산으로도 계산이 가능하다.

식 (9)에서 ${M}_{⊙}$=4로 놓고 P의 단위로 년, a의 단위로 AU를 사용하면 식 (9)는 단순히 4${P}^{2}$=${a}^{3}$ (11)이 된다. a는 변하지 않고 여전히 1이므로 따라서 식 (11)로부터 P=1/2이 되어야 한다.

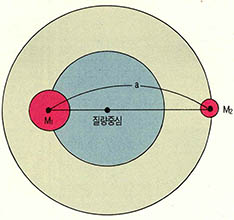
식 (9)는 전적으로 행성이 태양을 공전한다는 가정하에 얻어진 것이다. 이는 물론 태양과 행성의 질량 차가 너무 큰데서 얼마든지 정당화될 수 있다. 하지만 쌍성과 같은 경우 두 천체의 질량은 거의 비슷한 경우도 얼마든지 있으므로 식 (9)를 쓸 수는 없다. 두 천체의 질량이 ${M}_{1}$, ${M}_{2}$인 경우 식 (9)에 해당되는 케플러 법칙은 (${M}_{1}$+${M}_{2}$)${P}^{2}$=(4${π}^{2}$/G)${a}^{3}$ (12)이 된다. 단 여기서 a는 (그림 3)에서 처럼 두 행성 사이의 거리가 된다. 식 (12)는 고등학교 지구과학 교과서에서 상세히 다루어져 있으나 각자 유도하여 보기로 하자. 식 (9)는 식 (12)에서 ${M}_{1}$+${M}_{2}$=${M}_{⊙}$+m≒${M}_{⊙}$ (13)인 특수한 경우에만 해당되는 것임을 알 수 있다.

이번에는 지구가 현재의 공전 궤도를 유지하고 있는 상태에서 그럴리는 없지만 갑자기 지구의 질량이 4배로 불어났다고 하자. 그럼 지구의 공전 주기에는 어떠한 변화가 일어나는지 생각해 보자. 식 (13)에서 알 수 있듯이 지구의 질량은 4배 정도 늘어나서는 아무런 영향을 줄 수 없다. 왜냐하면 예를 들어 1억+1≒1억+4≒1억이기 때문이다. 따라서 이 경우 지구의 공전 주기는 변하지 않는다.

식 (12)에서 질량의 단위를 ${M}_{⊙}$, P의 단위로 년, a의 단위로 AU를 사용하면 식 (12)는 단순히 (${M}_{1}$+${M}_{2}$)${P}^{2}$=${a}^{3}$ (14)이 된다. 식 (14)야말로 태양계는 항성계에 모두 적용할 수 있는 일반적인 케플러 법칙이라고 말할 수 있다.
 

인공위성은 어떻게 도나?

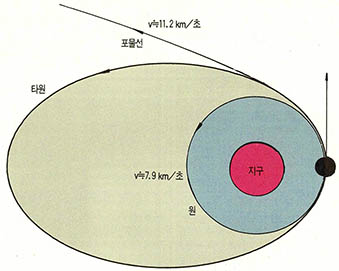
지구 둘레를 (그림 4)에서 처럼 원 궤도를 그리면서 등속원운동하는 인공위성을 생각해 보자. 인공위성의 속력을 v라고 하고 원 궤도의 반지름을 r, 지구의 질량을 M이라고 하면 구심력과 원심력이 비기는 경우의 v는 식 (8)과 유사하게 ${v}^{2}$=GM/r로 주어진다.

따라서 지구 표면의 바로 위에서는 r≒(지구 반지름)=6.3×${10}^{8}$cm를 만족해야 하므로 ${v}^{2}$-(6.67×${10}^{-8}$)(6×${10}^{27}$)/6.3×${10}^{8}$ v≒7.9(km/초) (16)가 된다. 즉 인공위성은 이 정도 속력을 유지해야만 지구 표면으로 떨어지지 않고 등속원운동을 계속할 수 있다.

인공 위성이 식 (16)의 속력보다 조금 더 빠른 초속도를 가지면 어떻게 될까. 인공위성은 그대로 원 궤도를 이탈해 지구로부터 탈출하게 될 것 같지만 사실은 그렇지 않다. 우리 지구의 경우 탈출 속도인 v≒11.2(km/초) (17)에 이르기 전에는 결국 (그림 4)에서 처럼 타원 궤도를 그리며 도로 지구로 끌려 돌아오게 된다. 탈출 속도에 이르러서야 인공위성은 비로소 포물선을 그리며 지구를 영원히 떠나게 되는 것이다. 식(17)의 탈출 속도는 식 (16)의 원운동 속도에다 2의 제곱근을 곱해서 얻어지며 이는 좀 더 어려운 물리학에서 유도된다.

이상으로 천체의 운동과 중력에 관한 기술을 마치고 다음 호부터는 별의 진화같은 현대 천문학 과정에 관하여 공부해 보기로 한다.
 

익힘문제 해답

(1)식 (14)에서 만일 우리가 ${M}_{1}$=16, ${M}_{2}$=0으로 놓고 P의 단위로 년, a의 단위로 AU를 사용하면 16${P}^{2}$=${a}^{3}$이 된다. a=1이므로 P=1/4, 즉 그 행성의 1년은 우리 지구 시간으로 3개월이 된다.

(2) 지구의 반경을 R이라 하고 인공위성이 추진되어 올라간 후의 공전 주기를 P이라고 하면 케플러 법칙으로 부터

${P}^{2}$/${(R+h)}^{3}$=${P'}^{2}$/${(R+2h)}^{3}$이므로

${P'}^{2}$=[${(R+2h)}^{3}$/${(R+h)}^{3}$]${P}^{2}$가 된다.

익힘문제

(1) 태양 질량의 16배나 되는 항성 주위에서 질량이 무시될 수 있는 가벼운 행성이 우리 지구와 똑같은 크기의 공전 궤도를 유지하고 있다고 하자. 그 행성에서의 1년은 우리 지구 시간으로 몇 년에 해당되는지 구하라.

(2)지구 표면으로부터 높이 h인 원궤도를 공전 주기 P로 돌고 있는 인공위성이 있다. 이 인공위성을 추진시켜 높이를 2배로 올리면 그 주기는 어떻게 되겠는가.