d라이브러리

금세기 최대의 성과인 상대성이론에 반기를 든 과학자도 없지 않았으나 아인슈타인의 이론은 오늘날에도 계속 입증되고 있다.

1915년에 아인슈타인(Einstein)이 발표한 일반상대성 이론은 한마디로 17세기에 뉴턴(Newton)이 만들었던 중력(만유인력)의 이론을 더 정밀한 이론으로 개량한 것이라고 말할 수 있다. 정밀한 관측이 가능해지면서 밝혀진 천문현상-예컨대 수성의 근일점(近日点)이동-을 통해 뉴턴이론의 오차(약1만분의 1%)를 제거할 수 있게 되었는데 그것이 바로 아인슈타인의 이론이다.

거꾸로 말하면 그 오차가 무척 미세한 크기였기 때문에 뉴턴이론이 2백년 이상이나 아무 탈 없이 인정돼 왔던 셈이다. 실제로 엄격한 정밀도가 필요하지 않은 천체(별 행성)의 운동을 설명하는 데는 오늘날에도 뉴턴이론이 그대로 적용되고 있다.

그러나 우주의 역사(특히 초기의 우주)나 검은 구멍(black hole)과 같이 엄청나게 큰 중력이 작용하는 경우에는 뉴턴이론이 무력해지기 때문에 일반상대성이론에 의지할 수밖에 없다.

「동등 원리」의 이해로부터

일반상대성이론을 이해하는데 가장 중요한 원리는 '동등(同等)원리'다. 이것은 중력이란 관측자가 타고 있는 '기차'(좌표계)가 가속도를 가질 때 느끼는 힘이나 다름 없다는 것이다. 기차가 가속되고 있을 때 그 속에 타고 있는 사람은 그 반대방향으로 힘을 받는 것처럼 느끼는데 이때 반대로 밀리는 가속도는 기차를 같이 탄 모든 사람에게 동일하다.

이 사실은 뉴턴에 앞서 갈릴레이가 물체의 낙하운동에서 발견했던 사실(모든 물체의 떨어지는 가속도가 동일하다는)을 연상시킨다. 이런 가속도의 동일성은 지구의 중력에 한정되지 않고, 일반적으로 중력이 작용하는 공간 즉 중력장(重力場)의 어디에서나 나타난다.

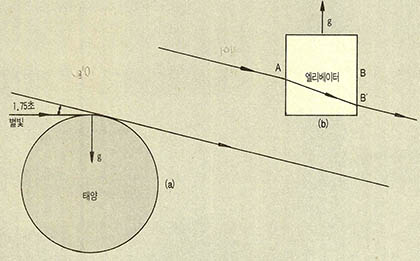
아인슈타인은 기차 대신 위로 가속되는 엘리베이터를 예로 들어 자신의 이론을 설명했는데 엄밀하게 말한다면 이 아인슈타인의 엘리베이터는 높이에 따른 중력의 차이가 나타나지 않을 정도로 작아야 한다. 즉 가속도의 동일성은 국소적(局所的)으로 성립한다.

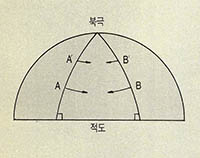
아인슈타인은 한 걸음 더 나아가서 중력이 공간의 구부러짐(曲率)에 연유하는 현상이라고 생각했다. 그 예로 구면(球面)으로 구부러진 지구표면을 생각해 보자. 두 사람이 적도위의 다른 두 점에서 정북(正北)으로(서로 나란히) 두 경선(經線)을 따라 움직인다면 북극에 가까워질수록 두 사람 사이의 거리는 줄어들어서 마치 두 사람 사이에서 서로 끌어 당기는 힘이 작용한 것처럼 생각될 것이다. 이 힘은 두 사람이 움직이는 공간(2차원의 구면)이 구부러진데 연유함을 쉽게 이해할 수 있다.

중력의 경우 이 구부러진 공간은 4차원의 시공간(時空間)이기 때문에 그 곡률의 표현이 복잡해질 수 밖에 없다.
 

일반상대론을 지지하는 네가지 증거

일반상대성이론을 검증하는 데에는 다음과 같은 네가지 방법이 쓰인다.

첫째는 중력에 의한 빛의 파장변화를 관찰하는 것이다. 빛이 태양에서 지구로 올 때 빛은 중력에 대항해서 일을 하게 되므로 그 만큼 에너지가 감소한다. 빛의 에너지는 진동수(파장)와 비례(반비례)하므로 지구에 도착한 빛은 진동수(파장)가 줄어서(길어져서) 본래보다 붉어진다. 이 효과는 지구의 중력장에서도 실험을 통해 밝혀졌다. 이것은 뫼스바우어(Mösbauer) 효과로 잘 알려지게 되었다.

둘째로 태양의 중력으로 인한 별빛의 구부러짐도 일반상대성 이론을 지지하고 있다. 이것은 1919년의 개기일식을 통해 확증됐다.

셋째로 수성의 근일점 이동도 아인슈타인의 이론을 입증한다. 이것은 오래도록 수성을 관측하는 천문학자의 두통거리였으나 상대성이론이 진통제가 돼 주었다. 실제로 그 값(${45}^{11}$/100년)은 아인슈타인이 산출해낸 값과 일치한다.

넷째로 전파의 메아리가 도착하는 시간도 상대성이론이 옳음을 증명한다. 이것은 지구에서 행성으로 보낸 전파중 직접 지구에 반사되는 것과 태양의 중력장을 우회하는 것과의 도착시간의 차이를 뜻한다. 이 차이를 통해 태양의 중력으로 인한 별빛의 구부러짐을 재확인할 수 있었다.

이 방법은 1964년부터 널리 실시됐는데 최근에는 1976년 화성에 도착한 무인탐사기 바이킹(Viking)을 이용, 0.2%의 정밀도로 이론과 관측치의 일치를 확인했다.

아인슈타인의 이론 이외의 중력이론으로 잘 알려진 것은 1961년에 발표된 미국의 브란스(Brans)와 디케(Dicke)의 이론이다. 이 이론은 중력상수 G를 시간적 공간적으로 변하는 양으로 다룬 것이 특색이다. 그러나 최근에 이뤄진 실험결과는 그것이 아인슈타인의 이론결과와 큰 차이가 없는 것으로 밝혀졌다. 그러므로 일반상대론을 대체할 더 좋은 이론은 아직까지 없는 것으로 생각된다.

아인슈타인은 중력이 빛을 구부리는 렌즈와 같은 작용을 한다고 예언했다. 즉 태양의 표면을 스쳐오는 별빛은 위로 가속된 엘리베이터에서 본 별빛처럼 구부러진다는 것이다. 그가 계산했던 별빛이 구부러지는 값은 1.75초였는데 실제로 1919년의 개기일식 때 관측된 값은 두 곳에서 1.61초±0.31초와 1.98초土0.12초로 나타나 그의 이론을 실증하기에 충분했다.

태양의 표면을 스쳐오는 별빛은 대개 햇빛의 밝기에 가려져서 볼 수 없지만 개기일식으로 인해 태양이 달에 완전히 가리어질 때에는 그 별빛을 관찰할 수 있다.

아인슈타인은 1936년에 만약 태양보다 훨씬 무거운 공과 같은 천체가 지구와 먼 은하 사이에 있고 이 세개의 천체가 완전한 기하학적 대칭성을 이룬다면 은하의 모습이 어떻게 보일 것인가를 예측해 보았다. 그는 먼 은하에서 오는 빛은 중간에 위치한 천체(은하나 은하들의 집단)의 중력 때문에(실험실 속의 렌즈실험처럼) 지구에서 먼 은하의 둥근 원환의 상(像)을 볼 수 있을 것이라고 제안했다.

그러나 이러한 대칭성이 이루어지지 않을 경우에는 먼 은하의 상이 두개, 또는 세개 네개로 나타날 것으로 계산됐다.

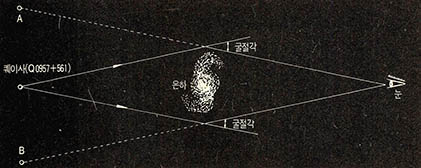
1979년 미국의 천문학자 월시(Walsh) 등은 약 60억광년 떨어진 먼 거리에 있는 퀘이사(quasar, 별처럼 보이는 작고 밝은 전파은하)에서 발사된 빛이 오는 도중에 위치한 한 은하의 중력작용을 받아 두개의 상으로 관측됐다는 사실을 밝혔다.

또 1988년에는 어떤 전파은하가 도중에 있는 은하들의 집단에 의한 중력의 렌즈작용 때문에 타원형의 상으로 관측되기도 했다. 이것은 1936년에 예언됐던 아인슈타인의 이른바 원환의 존재를 밝힌 최초의 증거로 받아들여지게 되었다.

천문학자들은 이렇게 중력의 작용 때문에 생긴 여러 개의 상이나 원환 또는 타원환을 우주의 신기루라고 부르고 있다. 아인슈타인의 일반상대론은 그 이론의 증거를 반세기를 넘는 오늘날에도 계속 찾아내고 있는 것이다.

보통 신기루는 사막의 상공에서 일어나는 이상한 굴절작용에 의한 대기현상으로 알려져 있다. 그러나 우주공간에 나타나는 이 거대한 신기루는 중력에 의한 빛의 굴절작용에 기인하는 것이다. 중력은 우리에게 친근한 힘이지만 때로는 검은 구멍이나 빛의 굴절현상과 같은 색다른 모습을 보여주고 있다.
 

아인슈타인의 실수

1917년 아인슈타인은 그의 중력이론으로 우주의 구조를 설명하려고 시도했다. 그는 우주가 하나의 전체라고 가정했고 정지된 것으로 생각했으나, 그의 이론대로 계산하면 우주가 정지상태에 있을 수 없다. 그래서 중력을 상쇄하는 척력(서로 반발하는 힘)을 중력의 방정식에 집어 넣었다.

그 척력을 나타내는 항의 상수Λ(＞0)는 '우주상수'로 불리고 있다. 한편 그의 방정식을 그대로 계산한 프리드만(Friedmann)은 팽창하는 우주의 해답을 얻었고, 1929년 허블(Hubble)은 망원경으로 먼 은하들의 후퇴운동을 관측, 우주가 팽창한디는 사실을 밝혀 프리드만이 내세운 우주론이 정당함을 뒷받침했다.

아인슈타인은 자기가 도입했던 우주상수를 취소하고 이것을 그의 큰 실수로 여겼다. 그러나 반세기가 지난 1980년대에 들어서 그의 실수마저도 다시 새로운 해석으로 각광을 받게 되었다.

그것은 프리드만 우주론이 지니고 있는 몇 개의 모순을 해결한 새로운 이론, 즉 급속팽창(inflation)이론이 발견된 데에서 비롯됐다. 이 급속팽창이란 우주초기의 극히 짧은 순간 동안(${10}^{-30}$초 이하)에 우주의 크기가 ${10}^{29}$배에서 10의 1억승(!)까지 엄청난 팽창을 한다는 뜻이다.

더욱 놀라운 사실은 여기에 필요한 에너지가 '진공'의 막대한 에너지라는 것이다. 이 진공의 에너지는 1㎤당 ${10}^{73}$g의 물질에 해당하는 것으로 이것은 태양보다 큰 별의 질량이 양성자(수소의 원자핵)의 크기에서 ${10}^{-13}$㎝ 크기까지 압축된 상황을 일컫는다.

오늘날의 양자물리학에 따르면 진공은 입자가 직접 관측되지 않는 상태지만 불확정성 원리에 따라 어느 최소한도의 불확정성(요동)이 존재한다. 이러한 진공의 요동은 수많은 가상적인 입자의 쌍(입자와 그 반대되는 입자)이 순식간에 생겼다가 또 서로 상쇄(0→+-→0)되는 과정으로 생각될 수 있다. 이 입자의 쌍은 실제 입자처럼 직접 관측되지는 않지만 그 효과는 원자속의 전자의 운동에 미치는 영향으로 검출된다.

그러므로 진공의 에너지는 0이 아니라 오히려 엄청나게 큰 값을 가질 수 있다. 그런데 아인슈타인이 잘못 도입했던 우주상수 Λ는 바로 이 진공의 에너지밀도를 나타내는 것으로 오늘날 재발견된 것이다.

사실 아인슈타인의 이론에서도 우주상수 Λ는 물질이나 복사의 에너지밀도와 대등한 역할을 하고 있으므로 이들과 무관한(즉 물질이 없어도 존재하는) 진공의 에너지밀도로 생각할 수 있었다.

과연 진공이 팽창한다는 것은 무슨 뜻일까.

보통 기체나 복사(광자의 기체)가 아무런 도움없이 팽창하면, 그 압력으로 벽을 밀어서 하는 일만큼 에너지가 감소해 에너지밀도가 내려간다. 그런데 진공의 경우 우주상수 Λ에 비례하는 일정한 에너지밀도가 깔려 있으므로 팽창한 부피에 비례해서 에너지가 증가하지만 에너지밀도에는 변함이 없다. 마치 칭기즈칸이 병사들의 배를 굶주리게 하지 않고 부유한 영토를 확대시킨 것과 비슷하다.

위의 두 경우를 비교하면 늘어난 부피에 비례해서 전체 에너지가 늘어나는 진공의 팽창에서는 기체의 경우와는 반대로 압력이 마이너스로 작용하는(즉 장력이 작용하는) 탄성체에 비유된다. 이는 고무줄이 늘어나는 것을 연상하면 쉽게 이해할 수 있다.

요컨대 진공의 에너지밀도가 일정(그렇지 않다면 '진공의 대칭성'이 성립하지 않는다)하다는 것을 달리 말한데 지나지 않는다.
 

천재가 남긴 숙제

그런데 이야기는 이것으로 끝나지 않는다. 그 까닭은 오늘날의 우주에서 Λ, 즉 진공의 에너지밀도가 엄청나게 작다는데 있다. 최근에 행한 은하들의 관측을 통해 알려진 에너지밀도는(물질밀도×${C}^{2}$, C는 광속도)는 ${10}^{-29}$g/㎤ 이하다. 따라서 진공의 에너지밀도가 달리 관측되지 않으므로 역시 이 값을 넘을 수 없다.

그런데 양자물리학에 따르면 진공의 에너지밀도는 우리가 생각하는 가상적 입자의 다양한 종류 때문에 진공의 에너지밀도는 입자가 전자라고 생각하면 ${10}^{6}$g/㎤일 것이다. 또 이론적으로 가장 무거운 입자일 때는 ${10}^{93}$g/㎤로 추정된다. 그러므로 오늘날의 관측치는 이론의 측정치보다 ${10}^{-122}$나 작다.

이러한 숫자는 이론으로나 상식으로나 설명하기가 곤란하다. 이것은 이미 1960년대에 소련의 젤도비치(Zeldovich)에 의해서 지적된 문제였다.
현재 세계의 많은 학자들은 이 문제를 해결하기 위해서 여러 가능성을 검토하고 있다. 그중 하나는 급속팽창이론에서 일어났던 진공의 상전이(에너지가 높은 진공에서 낮은 진공으로의 변이)가 여러번 과거에 일어나서 오늘날의 우주는 진공에너지가 거의 0에 가까운 상태에 다달았다는 것이다.

또 이러한 조정이 여러 우주들(우리가 직접 관측할 수 없을 정도로 멀리 격리된 우주들) 사이에 있음직한(?) 벌레구멍들의 연결이 과거에 이루어져서 우리 우주의 현황을 나타낸다는 견해도 등장하고 있다.

하여튼 아인슈타인의 이론은 많은 문제를 해결해준 한편 하나의 더 큰 숙제를 우리에게 남긴 셈이다.