d라이브러리

신이 주사위놀이를 좋아할 리 없다. -아인슈타인

20세기 물리학의 가장 큰 개가는 상대론과 양자론(量子論)의 탄생이라고 할 수 있다. 상대론과 양자론은 물리학에 조금만 관심이 있는 사람이라면 누구나 한두번 들어본 것들이다. 그러나 이 개념들을 이해하기란 그렇게 쉬운일이 아니다. 두가지 이론이 모두 우리의 상식이 통하지 않는 세계, 즉 지극히 빨리 움직이거나 굉장히 작은 세상에서만 그 참모습을 나타내기 때문이다.

플랑크상수가 뜻하는 것

현대물리학에서 양자론의 발자취를 빼면 연구다운 연구는 존재하지 않는다고 할 정도로 양자론은 물리학 가운데 확고부동한 자취를 남기고 있다. 양자론의 영향을 받지 않은 현대물리학의 분야는 없는 것이다.

양자론이 어떤 이론이며 우리의 생활과 사고에 어떤 영향을 주고 있는가를 이해하려면 우선 양자론을 공부하고 그 파급효과를 직접 터득하는 것이 가장 바람직하다. 그러나 그렇게 할 수 없는 많은 독자들을 위해 양자론의 한 단면을 소개하고 우리가 흔히 보고 듣는 일상생활에서 나타나는 여러 영향들 가운데 일부만 선택해 살펴보도록 하자.

양자론이란 무엇인가? 물리학에서 체계적인 계산을 시도하고 물체의 움직임에 대해 과학적인 이론을 처음으로 제시한 사람이 뉴턴임은 주지의 사실이다. 뉴턴의 이론은 우리들이 항상 접하는 이 세상을 이상화해 만든 법칙이다.

예를 들어 힘을 적게 가하면 그 물체의 속도 역시 조금만 변하며 힘을 전연 가하지 않으면 그 물체는 자기속도를 그대로 유지한다는 것이다. 이런 뉴턴의 법칙은 일상생활에서 주의깊게 관찰하면 쉽게 알 수 있는 일이다. 뉴턴의 물리학은 언제나 주어진 여건속에서(물리학에서는 주어진 초기조건이라고 한다) 어떤 물체의 운동을 정확하게(적어도 이론상으로는)계산할 수 있으며 그 물체의 속도 역시 정확히 산출된다. 속도 또는 속도×질량 (흔히 무게라고 하는 양)으로 나타나는 운동량도 가해지는 힘이 무엇인가에 따라 일정한 값을 갖게 된다. 예를 들면 길이가 L인 금속상자 속에 전자를 가둬 놓고 전압을 가해 가속시키면 우리는 일정한 운동량(혹은 속도)을 가진 전자를 만들어 낼 수 있다. 다시 말해 전압을 주기만 하면 원하는 운동량을 지닌 전자가 만들어진다고 믿었다.

그런데 이렇게 임의의 모든 값을 갖는 것이 불가능하다는 실험적인 사실이 20세기초에 발견되었다. 그 하나의 예가 막스 플랑크(Max Planck)가 지적한 흑체복사(black body radiation)에 관한 법칙이다. 그의 실험에 따르면 전자의 에너지나 운동량은 연속적인 것이 아니고 띄엄 띄엄한 특정한 값만이 가능하다는 것이다. 다만 그 값의 불연속성이 플랑크상수로 알려진 h라는 값으로 나타나는데 이 상수는 지극히 작은 수치다. 일상의 세상에서는 0이라고 해도 좋을 정도로 미미한 것이다.

따라서 일상생활에서는 모든 것이 연속적으로 느껴지고 뉴턴의 물리학이 맞아 떨어지는 것처럼 보이는 것이 오히려 당연하다. 불연속(不連續)적인 물리량을 주장하는 양자론은 미시적인 작은 양들이 중요시 되는 이론으로 출발했다. 양자론이 출범하자 곧 양자론에 있어서의 뉴턴의 운동방정식에 해당하는 슈뢰딩거(Schrödinger) 방정식이 탄생했다. 이 방정식의 대답을 통해 미시적인 원자의 세계를 이해하고 기술할 수 있게 되었다.

양자론에서는 자연현상을 슈뢰딩거 방정식의 해답인 파동함수로 나타낸다. 모든 물리량이 파동함수로 나타낸다. 모든 물리량이 파동함수로 표시되고 그 값은 확률로 정해진다는 것이 양자론의 골자다.

그러나 거시적인 물체의 운동에 양자론을 적용할 때는 고전적인 뉴턴의 이론과 다를 바 없다. 예를 들어 태양 주위를 돌고 있는 지구의 궤도를 구한다고 가정해 보자. 이때는 고전적인 뉴턴의 운동방정식이나 양자론적인 슈뢰딩거 방정식 중 어떤 것을 활용하더라도 그 결과에 차이가 없다.

그러나 미시적인 원자의 세계에서는 완전히 달라진다. 마치 지구가 태양을 중심으로 돌고 있듯 원자핵을 중심으로 도는 전자는 정해진 궤도에서만 회전한다. 전자는 회전속도를 마음대로 조절해 다른 궤도로 진입하는 자유를 갖지 못하는 것이다. 따라서 전자가 확률적으로 머물 수 있는 곳과 머물 수 없는 곳이 생긴다. 다시 말해 불연속적이고 배타적인 구조를 갖게 되는 것이다.

반도체의 생산에도

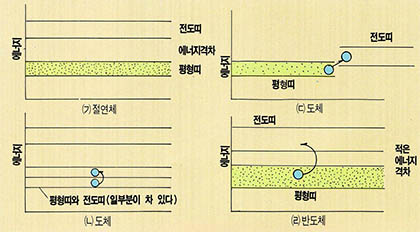
20세기 과학의 산물로 우리에게 가장 친숙한 것 가운데 반도체가 있다. 반도체는 TV, 컴퓨터, 전화기 등 모든 전자제품에 쓰이지 않는 곳이 없다. 원자의 세계에서 생기는 이 누적된 구조는 물질속에서 허용된 에너지의 띠를 만들고 있다. 물질속에 있는 전자들이 존재할 수 있는 이 에너지띠는 두 종류의 띠로 구성돼 있다. 전도띠(conduction band)와 평형띠(balance band)가 그것이다. 이 두 띠 사이에는 전자가 있을 수 없는 에너지 간격이 있다(그림).

이들 에너지띠의 상태가 어떻게 되어있는가에 따라서 도체 반도체 절연체가 결정된다. 평형띠와 전도띠 사이의 간격이 크고, 전도띠에는 전자가 전혀 없고, 평형띠는 완전히 꽉 찬 상태여서 전기가 잘 전도되지 않는 구조를 우리의 절연체(예를 들어 고무 같이 전기를 차단하는 물질)라고 부른다.

반면 평형띠의 전자가 완전히 차지 않아서 적은 전압만 걸어주어도 전자가 자유롭게 움직이거나 평형띠와 전도띠가 겹쳐있는 상태여서 전자가 잘 움직일 때 우리는 이를 도체라고 부른다. 구리(銅)같은 금속이 이런 경우에 해당한다.

반도체는 절연체와 도체의 중간쯤 되는 구조를 가진 물질이다. 평형띠는 절연체처럼 완전히 꽉 차있지만 그 위에 있는 전도띠와의 간격이 매우 좁아서 전압이 어느 정도 이상이 되면 평형띠의 전자를 전도띠로 올려놓는다. 이를테면 전류를 통하게 한다. 그러나 전압이 경계치 이하면 전도띠에 전자를 올려 보낼 수 없으므로 절연체처럼 행동한다. 이 기능을 이용하면 전류의 증폭, 스위치 역할등을 하는 반도체를 만들 수 있다. 이러한 에너지띠의 활약은 양자론의 기본구조를 응용한 것이다.

시위학생처럼

20세기 과학의 총아 가운데 초전도체가 있다. 국내에서는 아직 연구실에서나 볼 수 있는 물질이지만 선진국에서는 이미 실생활에 이용되고 있다. 예컨대 입자물리학을 연구하는데 필수적인 대형가속기의 부품 중 하나인 전자석(電磁石)은 초전도코일을 사용해 만들고 있다. 그리고 장차 자기부상열차 같은 초고속 열차가 좀 더 효율적으로 값싸게 달리게 하려면 초전도자석을 써야할 것이다. 또 초전도 현상을 송전에 이용하면 열의 손실없는 송전이 가능해진다. 이는 획기적인 산업혁신을 가져올 것이다.

잘 알려졌듯이 초전도란 금속을 극히 낮은 온도로(－2백73˚~－2백40℃) 냉각시킬 때 금속의 전기저항이 0이 되는 현상을 말한다.

도체 위를 흐르는 전류는 음(－)전하를 띤 전자의 운동에 의해 도선을 따라 사방팔방으로 전달된다. 이때 도체 내에 포함된 불순물에 의해, 또는 진동하고 있는 원자와의 충돌로 인해 그 전달과정이 방해된다. 이것이 바로 전자저항이다.

그러나 도체의 온도를 낮춰 어떤 임계온도 이하가 되면 원자의 진동에너지를 교환하는 과정에서 양자론적인 구조가 형성된다. 두개의 전자가 하나의 쌍이 되어 도체속으로 흘러가는 것이다. 이러한 많은 쌍들(이 원리를 발견한 쿠퍼교수의 이름을 따서 쿠퍼쌍이라고 한다)은 서로 얽혀 있다. 따라서 하나의 '쿠퍼쌍'(Cooper pair)의 운동을 방해하려면 그와 뒤얽힌 다른 많은 쌍을 함께 잡아야 한다. 그런데 그 힘이 미약해 쿠퍼쌍을 파괴하거나 멈추게 할 수 없다.

이는 마치 시위 진압 경찰이 데모를 막는 경우와 같다. 혼자 뛰쳐나오는 시위학생은 곧 저지당하고 말 것이다. 하지만 수많은 학생이 스크럼을 짜고 오면 그 대열은 쉽게 무너지지 않는다.

이러한 초전도현상 역시 양자론적인 구조가 만드는 거시적인 조화다.

양자론적인 현상은 동위원소의 붕괴시에도 볼 수 있다. 이 현상은 터널링(tunneling) 으로 알려진 양자론 고유의 것이다. 터널링현상을 이해하려면 먼저 양자론에서는 모든 것이 확률적으로 주어진다는 사실을 기억해야 한다. 실제로 터널링현상은 우리의 보통 상식으로는 이해하기 어렵다.

터널링현상에 도전하기 위해 높다란 담장으로 둘러싸인 형무소를 가정해보자. 담장의 높이가 10m, 어떤 날랜 수감자도 뛰어넘을 수는 없다. 바깥 세상이 그리워서 한 수감자가 담을 넘으려 뛰어보지만 번번이 담에 부딪쳐 실패하고 만다. 고전적인 뉴턴의 물리학에서는 이 사람은 영원히 이 담을 넘을 수 없다고 결론짓는다. 그러나 양자론에 따르면 이 미련한 수감자에게도 희망(?)이 있다. 1만경번, 즉 ${10}^{22}$번만 시도하면 이중 한번은 성공, 바깥 세상에 나갈 수 있다는 계산이 나온다. 이 수감자가 갑자기 높이뛰기선수가 되어 담을 넘은 것은 물론 아니다. 또 담에는 아무런 상처나 흔적도 없다. 그야말로 귀신처럼 담장밖으로 빠져나간 것이다. 마치 굴을 지난 기차가 산 너머로 뾰족 나오듯이 갑자기 나타날 수 있다는 것이다.

이렇게 터널링하는 확률은 ${10}^{22}$분의 1, 즉 1만경분의 1이라는 게 양자론의 결론이다. 어쩌면 독자들은 웃을지도 모른다. ${10}^{22}$번이란 천문학적 숫자고 ${10}^{22}$분의 1번이란 확률은 결코 일어나지 않는 일처럼 느껴질 것이다.

그러나 이런 '불가능'이 원자핵의 세계에서는 흔히 일어난다. 수감자가 형무소의 벽속에 갇혀 있듯이 양성자와 중성자들은 원자핵속에 갇혀 있다. 그런데 이 원자핵은 반지름이 ${10}^{-13}$㎝ 밖에 되지 않는다. 그 속에 있는 중성자는 빛의 속도의 10분의 1 정도의 속도로 움직인다.
그렇다면 이 중성자는 원자핵의 벽과 1초 동안에 3×${10}^{21}$번 충돌하고 있다. 이를 계산식으로 나타내면 $\frac{1}{10}$×(빛의 속도)÷(원자핵의 크기), 다시 말해 $\frac{1}{10}$×(3×${10}^{9}$㎝／초)÷(${10}^{-13}$)가 된다. 따라서 10초만 기다리면 3개의 중성자가 원자핵을 뚫고 나오게 된다. 라듐 우라늄 등 방사선 동위원소에서 방출되는 중성자는 이런 원리를 활용, 밖으로 나온다. 이를테면 양자론의 산물인 것이다. 따지고 보면 이 동위원소들이 의료원에서 암치료를 위해 쓰이고 있는 것도 양자론의 덕택이라 할 수 있다.

사고체계까지 바꿔 놓기도

양자론은 그야말로 모든 자연현상에 영향을 미치고 있다. 현대물리학의 전반에 걸쳐 크고 작은 관련을 맺고 있는 것이다. 양자론이 물리학에 미친 영향이란 말 자체가 어찌보면 모순이다. 왜냐하면 현대물리학이 바로 양자론 그 자체이기 때문이다.

양자론이 나오기 이전의 물리학에 양자라는 말만 붙이면 현대물리학을 총망라할 수 있다. 예를 들어 보자. 옛부터 알려진 광학(光學), 즉 빛이 굴절하고 회절하는 현상을 다루는 광학 앞에다 양자를 붙인 양자광학은 그 핵심이 레이저다. 그래서 흔히 레이저 물리라고 불리고 있다.

다른 예로 전자기의 상호작용을 다루는 학문을 전기역학이라고 한다. 여기다 양자를 덧붙이면 양자전기역학(quantum electro dynamics)이 된다. 이 양자전기역학은 현대물리학 뿐만 아니라 모든 과학중에서 가장 아름다운 체계를 지니고 있어 우리 인류가 가장 정확하게 이해하고 있는 과학의 하나다. 아무튼 이 양자전기역학은 20세기의 석학들, 페인만(R. P. Feynman) 슈빙거(J. Schwinger) 도모나가 (朝永振一郞)로 하여금 노벨상을 타게 한 활동무대가 되기도 했다.

양자론이 비단 물리학에만 영향을 끼친 것은 아니다. 현대과학 어느 분야를 막론하고 양자라는 표현이 붙지 않은 곳이 없다. 예컨대 양자화학 양자생물학(혹은 분자생물학) 등 양자라는 표현은 20세기 과학의 상표처럼 돼 있다.

양자론은 우리의 사고자체를 바꾸어 놓기도 했다. 양자론이 처음 선보였던 20세기초만 해도 물리학은 원인이 있는 곳에 반드시 정해진 결과가 있다는 인과론(因果論)을 굳게 신뢰하고 있었다. 저 유명한 포앙카레의 말처럼 현재의 모든 상태를 알면 앞으로 다가올 이 우주의 모든 일을 계산할 수 있다고 믿었던 것이다. 다분히 원리적이고 이상적인 말이지만 주어진 뉴턴의 방정식의 해답을 찾고 그 당시의 조건을(초기조건) 다 고려하면 모든 미래는 알 수 있다는 생각이었다.

그러나 양자론이란 새로운 이론체계는 고전적인(뉴턴적인) 세계관을 완전히 깨버렸다. 모든 일이 미리 확정된 운명적인 길을 걷는 것이 아니고 확률만이 주어질 뿐이라고 본 것이다. 한마디로 더 열려진 생각을 우리에게 심어준 셈이다.

저 유명한 아인슈타인은 자신이 양자론의 발전에 결정적인 기여를 했음에도 불구하고 이런 확률적인 개념을 좋아하지 않았다. 아인슈타인이 양자론의 확률적인 해석을 주사위에 비유, 자신의 심정을 토로한 유명한 말이 있다. "신이 주사위 놀이를 할리가 없다"(God does not play dice).

그러나 현대과학이 제시하는 모든 실험적인 사실은 신이 주사위놀이를 할 뿐 아니라 그것도 수많은 주사위를 항상 던지고 있음을 보여준다.