d라이브러리

고학년이 되면서 과학지식이 늘어갈수록 나에겐 제일 궁금하게 생각되고 강한 호기심을 유발시킨 것은 시간과 공간의 의미였다. 신비스럽기까지도 하면서 이 문제는 나에게는 너무나 막연하고 어려웠다. 그래서 시간이 날 때마다 공상과 상상을 하여 정리한 내용을 소개하고자 한다.
1차원 좌표(점), 2차원 좌표(평면), 3차원 좌표(공간)를 만든 원리대로 서로 수직인 4개의 직선으로 4차원 좌표를 만들려면 3차원(공간좌표)에 새로운 축(시간축)을 수직으로 첨가하면 된다. 즉 이 좌표는 어떠한 공간이 시간축의 단 하나의 점에 위치하고 시간의 연속적 흐름에 의해서 공간이 이동하는 것을 뜻한다.
 

공이 떨어지는 것을 예로 든다면 꼭대기에서 아래로 공이 떨어질 때 각 시각마다의 공의 위치와 상태를 보면 모두 다르다. 즉 이 하나의 시간점에 정해진 각각의 상태를 각기 다른 공간이라 할때 결국 공의 낙하는 각 시간마다 정해진 사건(공의 위치)들의 연속적 흐름이라고 할 수 있다.
 

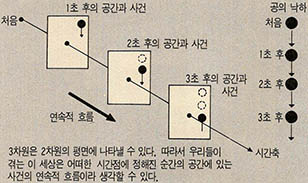
마치 영화필름처럼 한 컷 마다의 인물의 동작은 다르나 그것들의 연속된 동작이 곧 한편의 영화장면이 되는 것처럼 위의 4차원 좌표는 공간의 시간좌표 이동이라 할 수 있다. 그러나 이런 식의 좌표는 하나의 시간축에 있을 수 있는 사건의 다양성을 설명하기엔 조금 불충분하다.
예를 들어보자.

현재시각 오후2시, 나는 우산이 없어서 비를 맞고 있다. 우산을 가지고 나왔더라면…. 과거로 가서 우산을 준비해야겠다고 생각하고 과거(오전 10시)로 되돌아 갔을 때, 다음 두가지 경우를 생각할 수 있다.

첫째 타인의 시간과 공간은 변함이 없고 나만이 시간을 거슬러 올라가서(오전 10시로) 우산을 준비해서 오후 2시에는 비를 피할 수 있게 된다.
둘째 현재에서 과거로 가보니 오전 10시의 내가 있었다. 우산을 준비하라고 해서 나는 오후 2시가 되어 비를 피할 수 있게 됐다.

그런데 이 실험에서 보면 맨처음 비를 맞은 나와 과거로 되돌아가서 우산을 준비해서 비를 피하게 되는 나는 모두 동일시간(오후 2시)에 존재하게 된다. 또 오전 10시의 과거로 거슬러 올라갔을 때 그곳에는 원래 있던 나와 현재에서 과거로 거슬러간 내가 함께 존재하게 된다. 동일 시간에 생길 수 있는 사건의 다양성을 설명하기에 위의 좌표계가 불충분하다.

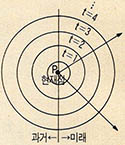
따라서 이런 문제점을 해결하기 위해서는 하나의 시각에서 여러 개의 사건을 설명할 수 있는 새로운 좌표가 필요했다. 곰곰히 생각하다가 우연히 동심원을 생각했다.(그림3)

점P(현재점)으로부터 동일시간을 연결하면(그림1)과 같은 동심원 모양의 파가 된다. 즉 점P에서 미래로 가는 사건의 수는 무수히 많고 임의의 시간에서 일어날 수 있는 사건의 수도 무수히 많게 된다.

예를 들어 시각 t=2일 때 일어날 수 있는 사건은 t=2인 동심원의 곡선위의 모든 점이므로 무수히 많다. 따라서 앞의 우산 실험의 동일시간에서의 사건의 다양성을 이 좌표로 설명할 수가 있게 되었다.
 

그러다 우연히 아인슈타인의 상대성이론 중 시간은 물체의 운동속도에 따라 차이가 날 수도 있다는 말에 착안을 해서 그것을 설명할 좌표를 만들기로 했다. 보통의 직선좌표로는 잘 되지 않아 곡선좌표를 생각했다. 곡선 OC위에 좌표를 0~C(광속)까지 분할해서 잡고 그 위의 임의의 점 ${V}_{0}$를 잡으면 (t’=$\sqrt{1-Vo²/C²}$)이 되게 곡선 OC를 그린다.
 

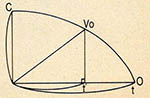
즉 정지한 물체(V=0)인 물체의 시간t와 (V=${V}_{0}$)의 속도로 움직이는 물체의 시간 t’와의 관계를 나타내는 공식으로 t-t’의 시간차가 발생한다(상대성이론). 이것을 앞의 시간좌표와 결합하면 (그림5)처럼 된다. (그림4)의 시간평면 중 임의의 사건을 택하고 그 사건의 직선위에 (그림5)의 좌표를 세우면 V=0로 움직이는 물체(정지상태의 물체)는 순리적인 시간의 흐름대로 t시간에 이르는데 V=${V}_{0}$로 움직이는 물체는 곡선좌표에서 아래평면에 내린 수선과의 교점 t’만큼의 시간이 흐른다.
 

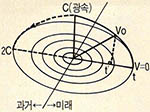
따라서 정지된 물체와 움직이는 물체 사이의 시간차를 알 수 있다. 또 V가 계속 증가하여 V=C(광속)이 되면 t는 현재점 그대로(t=0)가 되어 시간 정지상태가 된다.

그리고 가설로서 V가 C(광속)보다 빠를 때는 오른쪽 대칭형과 값은 같으면서 다만 시간의 흐름이 (-)즉 과거로 가는 것이다. 만약 V=2C가 되면 시간은 정지된 상태의 빠르기와 똑같은 상태로 과거로 간다.

시간은 결코 과거로 흐르지 않는다

'시간의 파괴'라는 학생의 글을 읽고, 우선 이 학생의 실수를 지적하기에 앞서, 학생의 과학에 대한 깊은 관심과 순수성에 박수를 보내고 싶다. 여러 과학서적을 읽고 많은 생각을 하여 그 생각을 정리하고 참고 했으리라 본다. 그러나 상상이란 구속이 없으므로 그에 따른 오류나 실수가 많이 일어나며 이 학생 역시 이 범주에 속하는 것 같다.

과학이란 사물의 이치를 실험과 검증을 통하여 입증하고 이해하여 그 근본을 논리적으로 설명하는 학문이다. 특히 물리학은 사물의 근본이치를 수학이라는 매개체를 통하여 기술할 뿐만 아니라 물리계의 모든 현상의 타당성을 논리적으로 설명할 수 있어야 한다. 다시 말해서 수학(기하학을 포함해서)이 곧 물리는 아닌 것이다. 상상이 과학발전의 한 기틀이 될 수는 있으나 이것이 곧 과학발전을 의미하는 것은 아니므로 여기에는 반드시 논리적 타당성이 첨가되어야 하겠다.

우리는 차원을 무한차원까지 확장하여 전개할 수 있으며 시간도 이 차원의 범주에 속한다. 이러한 차원의 확장은 우선 과학적인 타당성을 갖고 있어야 한다. 물리학도 그 테두리를 벗어날 수는 없는 것이어서, 공간이나 차원의 확장을 물리적으로 완전히 설명할 수 있을 때 물리학은 비로소 그 공간과 차원을 인정하는 것이다.

'시간은 살과 같이 지난다' 또는 '시간은 유수와도 같다'라는 말이 있다. 그러나 어디까지 이 말은 삶을 통한 경험과 감각에서 우러나온 말이지 시간의 흐름을 눈으로 확인해서 생긴 말은 아니다. 따라서 시간이 물리적으로 중요한 변수임에는 틀림이 없으나 이것을 그림으로 그릴수는 없으며, 특히 학생의 그림처럼 공간축과 교차되는 시간축을 그릴수는 더더욱 없는 것이다. 또 시간의 좌표를 동심원으로 설정한 착상은 매우 재미있는 생각이었으나 이것은 다른 문제점을 야기시킨다.

상대성이론에 따르면 명백하게 시간지체(time delation)가 설명된다. 그러나 어디까지나 이것은 '시간흐름'의 지연이며, 시간의 역류가 아님을 알아야 하겠다. 즉 속도가 광속에 접근하면 접근할수록 시간의 흐름이 늦어지는 것이지 시간이 거꾸로 흐르는 것이 아니라는 것이다. 다시 말해서 미래에서 현재로, 현재에서 과거로 가는 것이 아닌 것이다. 따라서 학생이 설정한 동심원의 반경의 커짐에 따른 시간의 설정은 잘못된 것이다. 또한 과거 현재 미래의 기준이나 경계선 역시 애매모호하다.

또 한가지 학생의 착각은 다음과 같다. 우리가 학생이 설정한 좌표축을 적용하여 광속으로 여행하고 있다고 가정해보자. 또 이 시점에서 과거로 되돌아가보자. 또 이 시점에서 과거로 되돌아가보자. 학생의 좌표공간대로라면, 과거로 되돌아 가려면 우리의 여행속도의 투영 또는 속도의 크기 역시 작아져야 하는데, 그러려면 속도는 광속보다 작아져야한다는 결론이 나온다. 따라서 우리는 다시 시간의 흐름을 느끼게 되며 따라서 우리는 과거로 되돌아 갈 수 없다는 결론을 얻게 된다. 왜냐하면 시간은 한쪽으로면(아직까지는!) 흐르는 속성을 갖고 있기 때문이다. 결국 과거로 돌아가기 위해서는 -t를 유도해내야 하는데 그 때문에 동심원 좌표공간으로는 과거로 돌아가지 못하게 되는 것이다. 따라서 학생이 설정한 좌표공간은 잘못된 것이라고 하겠다.

과학적 체계가 없는 학생의 생각이므로 얼마든지 오류가 일어날 수 있다. 또 자신의 생각과 상상을 여러 사람과 같이 생각해보려는 의도는 좋았지만 주변의 여러 사람들과 조금 더 상의해보고, 숙고해 봄이 바람직하지 않았나 하는 생각이다. 왜냐하면 과학적 체계없이 발표하는 것이 오히려 어린 학생에게 선입관을 심어 줄 수도 있기 때문이다.