d라이브러리

똘똘 뭉친 휴지와 가지런히 접은 휴지 중 어느 쪽이 더 휴지를 적게 쓸까? 다소 황당한 듯 보이는 이 질문의 답을 잠깐 생각해보자. 뭐라고 답을 냈는가.

2019년 미국의 소셜 뉴스 웹사이트 ‘레딧’에 이 질문이 올라오자 사용자들은 ‘당연히 접어야지, 뭉친 휴지로 닦는다는 개념 자체를 이해하지 못 하겠다’, ‘접을 시간이 어디 있냐, 뭉쳐야지’ 등 팽팽한 대립 반응을 보였다. 

 

그러던 2020년 4월, 물리학자 사무엘 노바리오가 수학 모형을 세워 이 질문에 답했다.

 

 

노바리오는 휴지를 찢어지지 않게 하면서 오물을 처리하는 데에 쓰는 휴지의 총량을 최소화한다는 목표를 세운 뒤, 1번 닦을 때 오물이 가장 많이 묻어나오는 휴지의 형태를 찾고자 했다. 그리고 면적이 넓을수록, 많이 주름질수록 오물이 잘 닦인다고 보고, 각 휴지의 상태에 따라 면적과 주름의 정도, 휴지 뭉치의 강도가 어떻게 변하는지 비교했다. 

 

그 결과 접은 휴지는 같은 양으로 더 큰 면적을 만드는 장점이 있었지만, 주름진 정도가 낮으며 닦다가 찢어질 확률이 더 높았다. 이에 반해 뭉친 휴지는 주름진 정도와 견고함이 높았지만, 같은 양으로 만드는 면적이 좁았다. 따라서 그는 같은 양의 휴지가 있을 때 가장 이상적인 방법은 뭉치는 것과 접는 것 그 사이에 있을 거라며 반은 뭉치고 반은 접은 ‘하이브리드 휴지’를 제안했다. 

 

 

하이브리드 휴지가 정말 우리 엉덩이와 환경을 지켜줄 확실한 대안일까? 최적화 문제를 풀려면 변수 사이의 관계식을 정확히 알아야 하는데, 노바리오의 설명에는 이 부분이 빠져 있다. 또 접거나 뭉치는 등의 서로 다른 방법을 썼을 때 면적과 주름이 변하는 정도가 정확히 어떤 식에 의해 변하는지 알아야만 하는데 그 부분도 설명에서 빠져 있다. 

 

하지만 질문에 수학적으로 사고해 답을 도출한 점은 흥미롭다. 이 질문에 더 정확한 답을 찾고 싶다면 개인의 닦는 스타일, 힘주는 압력, 휴지 브랜드 등을 따져 실험해보자. 의미 있는 변수를 산정해 계산한다면 노바리오보다 더 정확한 답을 끌어낼 수 있을 것이다. 

 

 

 

 

이 질문은 2014년 수학자 리아 시몬즈가 수학 전문 유튜브 채널 ‘넘버파일’에서 소개한 것이다. 더러운 화장실과 깨끗한 화장실이 무작위로 뒤섞여 있는 상태에서 한 칸씩 열어보며 지나갈 때 몇 번째에서 멈추는 것이 가장 좋을지 묻는 ‘최적 멈춤’ 문제다. 

 

제한 조건이 없다면 모든 칸을 확인한 뒤 가장 깨끗한 칸을 선택하면 되겠지만, 한 번 지나온 칸은 절대 돌아갈 수 없으니 무작정 끝까지 열어보다가는 지나온 칸보다 나쁜 칸을 선택할 확률이 높다. 반대로 너무 빨리 선택하면 더 나은 화장실에 갈 기회를 놓쳐버릴 수 있다. 그러면 몇 번째에서 멈추는 것이 가장 깨끗한 화장실을 선택할 확률을 최대로 만들까?

 

문제를 수학의 언어로 바꾸고, 문제에 나온 조건들을 잘 정리해 본격적으로 풀어보자.

 

 

경우➊ 화장실은 3개, 처음 칸은 제외(n=3, k=1)

 

 

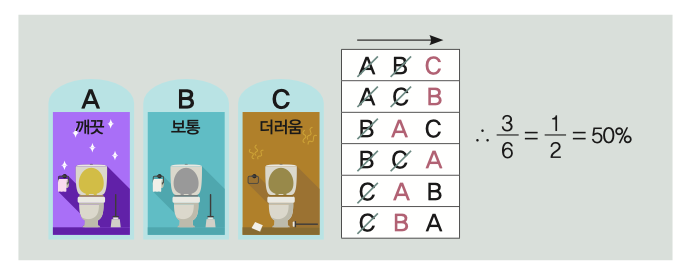
3개의 화장실을 나열하는 경우의 수는 3!(=6)이고, 각 경우에 선택하는 화장실은 위쪽 표와 같다. 따라서 가장 깨끗한 화장실 A를 고를 확률은  1/2=50%다. k=0, k=2일 때 확률은 둘 다  1/3이므로, 화장실이 3칸일 때는 첫 번째 칸을 보고 그 칸보다 깨끗한 칸이 나오면 바로 멈추는 것이 최적의 전략이다.

 

경우➋ 화장실은 4개, 처음 칸은 제외(n=4, k=1)

 

 

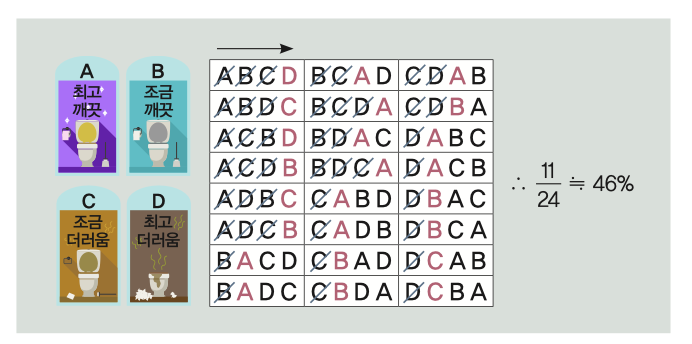
4개의 화장실을 나열하는 경우의 수는 4!(=24)이고, 각 경우에 선택하는 화장실은 위쪽 표와 같다. 따라서 가장 깨끗한 화장실 A를 고를 확률은  11/24≒46%다. k=0, k=2, k=3일 때 확률은 각각  6/24, 10/24, 6/24 이므로, 화장실이 4칸일 때도 첫 번째 칸을 보고 그 칸보다 깨끗한 칸이 나오면 바로 멈추는 것이 최적의 전략이다.

 

 

➌ 화장실이 n개일 때 제외할 칸(k)의 값

 

 

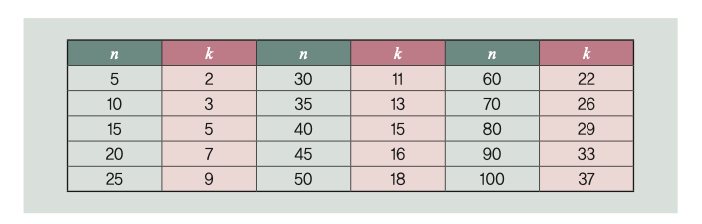
같은 방법으로 전체 화장실의 개수(n)가 무한히 많아질 때를 따져보면 둘러봐야 할 화장실의 개수(k)는 전체의 37%에 가까워진다. 화장실이 100칸이라면(n=100) 37칸을, 1000칸이라면(n=1000) 370칸을 열어보는 것이 최적 멈춤이다. 

 

혹은 깨끗한 화장실을 고를 확률을 일반식으로 나타내고 이 식이 최대가 되는 값을 찾는 방법도 있다. 다만 이 식은 다소 복잡한 데다 최댓값을 찾기 위해서는 미적분을 알아야 하므로 오늘은 결론만 알고 넘어가기로 하자. 

 

확률 식을 풀면 k값은 n/e으로 구해진다.  e ≈ 0.3679이므로 역시 전체의 약 37%를 열어본다는 결론에 이른다.

 

즉 전체 화장실에서 37%는 열어보기만 하고 이후에 열어본 칸 중 지금까지 본 것보다 깨끗한 화장실이 나오면 무조건 선택하는 것이 최고의 전략이다!

 

 

길을 걷다가 날아가는 새의 똥을 맞을 확률은 얼마나 될까? 맞을 확률이 희박하기에 진짜 맞게 되면 운수 나쁜 날이라며 투덜거리게 될 텐데, 이 확률을 직접 계산한 수학자가 있다. 

 

2015년 수학자 피터 올로프슨은 미국 뉴욕 거리를 지나가다 비둘기 똥에 맞을 확률을 계산했다. 그는 하늘에서 수직으로 내려다본 사람의 머리와 어깨 부분의 평균 넓이, 사람과 비둘기가 움직이는 면적, 면적당 날아다니는 평균 비둘기 수, 시간당 비둘기의 배변 횟수 등을 계산에 이용했다. 

 

 

계산 결과, 뉴욕 시내를 2시간 동안 멈추지 않고 돌아다닌다면 20%의 확률로 비둘기 똥에 맞을 수 있다고 한다. 그렇다면 비둘기가 많기로 유명한 우리나라 서울에서 비둘기 똥에 맞을 확률은 얼마일까? 올로프슨의 방법을 따라 확인해보자.

 

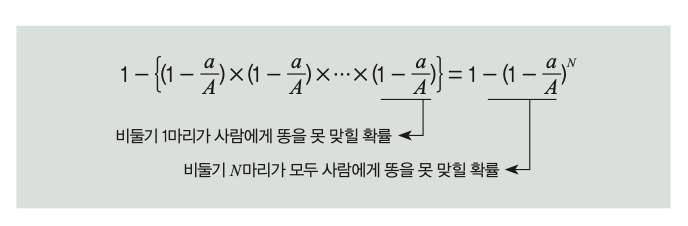
먼저 위에서 내려다본 사람의 머리와 어깨너비를 a, 이 사람이 움직인 범위의 넓이를 A라고 하자. 그러면 A 구간을 날고 있는 비둘기 1마리가 똥으로 사람을 맞힐 확률은 a/A 로 구할 수 있다. 만약 A 구간에 비둘기가 2마리 있다면 둘 중에 최소 1마리만 사람을 맞힐 확률을 구하면 되는데, 전체 확률에서 2마리 모두 맞히지 못할 확률을 빼면 된다. 따라서 비둘기가 N마리 있다면 사람이 똥에 맞을 확률 1에서 모든 비둘기가 사람을 맞히지 못할 확률을 빼면 된다. 

 

2009년 한국조류보호협회가 발표한 서울시의 비둘기 수는 약 3만 5,000마리다. 올로프슨은 비둘기가 하루 평균 약 21%의 시간 동안 날아다닌다고 했으니 서울시를 기준으로 하면 시간당 날고 있는 비둘기 수는 평균 7,350마리고, 서울시의 면적이 605km²이므로 100m²의 공간에 시간당 날고 있는 비둘기 수는 평균 1.2마리다.

 

 

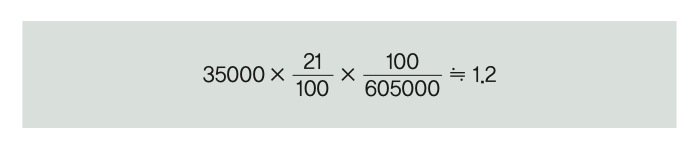
이제 N을 새롭게 정의해서 단순한 비둘기 수가 아닌 어떤 시간 동안 걷는 사람에게 노출된 비둘기 똥의 수로 보자. 올로프슨은 수의사의 의견과 기존 연구를 바탕으로 비둘기가 12분마다 1번씩 똥을 누는 것으로 가정했다. 그러면 서울 시내 100m²를 사람이 2시간 동안 쉬지 않고 걸어 다니는 동안 노출되는 평균 비둘기 똥의 수는 다음과 같다.

 

 

따라서 수직 면적 0.1m²인 사람이 서울 시내 100m²를 2시간 동안 돌아다닐 때 비둘기 똥에 맞을 확률은 1-(1-a/A)^N=1-(1-0.1/100)¹²=0.01193, 약 1.2%다. 

 

2023년 기준 서울시 전체 인구가 약 939만 명이니 약 11만 2,000명이 길을 걷다 비둘기 똥에 맞을 수 있다. 생각보다 가능성이 큰일이므로, 비둘기 똥에 맞았다고 너무 기분 나빠하지 말자.