d라이브러리

만화에서 김재희 교수는 매일 관측한 지구와 토끼 행성의 거리가 ‘피보나치 수열’을 따른다고 보고 토끼 행성의 위치를 예측했어요. 피보나치 수열이란 처음 두 항이 1, 1일 때 앞의 두 수의 합이 바로 뒤의 수가 되는 수의 배열을 의미해요.

피보나치 수열을 처음 언급한 문헌은 기원전 5세기 인도의 수학자 핑갈라가 쓴 책으로 알려져 있어요. 이후 1202년 이탈리아의 수학자 레오나르도 피보나치가 자신의 책 <;주판서>;에 피보나치 수열을 소개해 유명해졌습니다. 그는 어느 날 토끼가 새끼를 낳고 번식하는 모습을 보다가 호기심을 갖고 한 문제를 만들었어요. 

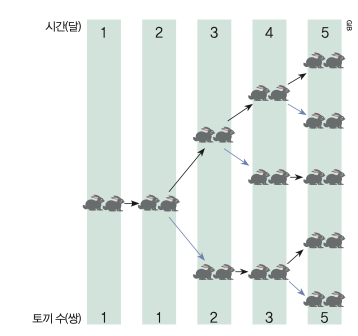
‘갓 태어난 토끼 한 쌍이 있다. 이 토끼 한 쌍은 두 달 후부터 매달 암수 한 쌍의 토끼를 낳는다. 새로 태어난 토끼들도 2달 후부터 매달 1쌍의 토끼를 낳는다면, 1년 동안 태어난 토끼는 모두 몇 쌍일까? 이때 토끼는 죽지 않는다고 가정한다.’

답을 찾았나요? 아래 표를 보면 앞의 두 수의 합이 바로 뒤의 수가 되는 규칙이 눈에 보일 거예요. 이 규칙에 따르면 1년(12달) 후 토끼 쌍의 수를 쉽게 구할 수 있어요. 233쌍이에요. 

당시에 이 수열은 피보나치 수열로 불리지 않았지만, 19세기 프랑스 수학자 에두아르 뤼카가 피보나치 수열이라고 이름을 붙였어요. 수열의 항 사이에 성립하는 관계식인 ‘점화식’을 이용해 간단히 나타낼 수 있습니다. 

다시 만화의 내용으로 돌아올게요. 토끼 행성의 위치는 오후 10시를 기준으로 순간 이동하듯 위치가 변해요. 오후 10시 전까지는 그 전날 오후 10시에 이동한 그 위치에 있어요. 5일째 거리를 측정할 때 시각이 오후 9시 59분이기 때문에, 4일째 오후 10시 이후에 관측한 거리와 같을 거예요. 날짜별 기록을 오후 10시 1분을 기준으로 정리해 나열하면 100, 93, 86, 72, 51, 16, -40이 돼요.

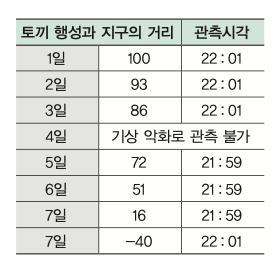
3일째까지만 보면, 토끼 행성과 지구와의 거리는 100 - 7(n - 1) = 107 - 7n(n = 1, 2, 3)으로, 등차수열을 따른다고 볼 수 있어요. 초항이 100이고 등차가인 등차수열인 거지요. 하지만 4일째부터 갑자기 전 항과 그다음 항이 14, 21, 35, 56순으로 차이가 커져요. 다시 1일부터 거리의 차를 나열해보면 7, 7, 14, 21, 35, 56이에요. 발견하셨나요? 연달아 있는 두 수의 합이 바로 뒤의 수가 되는 수였습니다. 여기에서 김재희 교수는 힌트를 얻은 거예요.

이를 식으로 나타내면 100 - 7(F_{n + 1}로 표현할 수 있어요. F_n은 앞에서 언급한 피보나치 수열을 말해요. 예를 들어 F₃은 2니까, 토끼 행성과 지구와의 거리 수열의 2항은 100 - 7(2 - 1)로 93이에요. 그 뒤 항까지 손쉽게 계산할 수 있습니다. 

만화에서 재미 요소로 등장한 피보나치 수열은 사실 꽃잎의 수, 솔방울과  해바라기 씨앗의 배열, 앵무조개 껍데기 등 자연에서 발견할 수 있어요. 이 수열은 사람들이 자연을 해석하는 데 도움을 줬답니다.

이처럼 수열은 세상을 이해하고 예측하는 데 큰 역할을 해요. 과거로부터 현재까지의 데이터 변화처럼 가까운 미래도 변할 거라고 가정하고 예측할 수 있거든요. 경제학에서도 미래의 경제성장률, 출산율 등을 예측할 때 수열을 많이 사용해요. 과거의 수열을 보고 어느 정도 오차를 감안해 미래를 예측하는 거예요. 물론 수열의 규칙과 다르게 예외적인 경우가 있을 수도 있지만요. 

마지막으로 만화에서 행성의 움직임과 관측방법은 실제와는 많은 차이가 있어요. 오늘날 과학의 발전으로 인해 행성의 위치를 굉장히 정확히 예측할 수 있어 만화에 등장한 오류와 해프닝은 일어 나지 않을 거에요. 재미를 위해 꾸며낸 이야기임을 기억해 주시면 고맙겠어요.