d라이브러리

기하학은 수학에서 가장 오래된 분야 중 하나다. 이는 ‘재는 행위’에서 혹은 ‘재기 위해’ 발전해왔다. 그렇다면 기하학에서 ‘재다’는 어떤 의미일까? 수학자와 인문학자가 각자의 시선에서 답하며 역사적, 수학적 맥락을 이야기 나눠 본다.

첫 번째 질문 기하학은 재는 학문인가?

수학자 : 이번 시간부터 3화에 걸쳐 기하학을 주제로 이야기를 나눠볼 텐데요. 먼저 기하학의 어원에서부터 시작하면 좋을 것 같아요. 기하학이라는 단어는 어디서부터 왔나요?

인문학자 : 기하학은 영어로 Geometry예요. 그 어원은 고대 그리스어 Γεωμετρία(Geometria)에서 찾을 수 있어요. 땅(Geo)을 재(Metria)는 학문이란 뜻이지요. 고대 그리스는 고대 이집트와 중동에서 수학을 받아들여 발전시켰어요. 고대 이집트에서는 땅의 넓이에 비례해서 세금을 거둬들였는데, 나일강이 주기적으로 범람하는 바람에 이때마다 땅의 경계선이 지워져 구획을 다시 측정해야 했어요. 그래서 땅을 재는 게 굉장히 중요했지요.

우리가 쓰는 기하학이라는 말도 영어에서 유래를 찾을 수 있는 한자어예요. 중국에서는 어떤 외래어를 번역할 때 발음이 비슷한 글자 중 의미가 통하는 걸 써요. 기하학도 마찬가지로 영어 Geometry(지오메트리)와 유사한 중국어 발음인 幾何(지허)라는 말로 표현했어요. 얼마 기(幾)와 어찌 하(何)를 써서 ‘어떤 대상이 어느 정도 되는지를 어떻게 재서 구할 것이냐’라는 뜻이지요.

수학자 : 우리는 보통 ‘재다’라는 말을 떠올릴 때, 자나 각도기와 같은 도구를 사용한 측정을 생각하는데요. 고대에는 ‘재는’ 행위가 어떻게 이뤄졌나요?  

인문학자 : 고대에도 무언가를 잴 때 도구를 사용했어요. 그런데 현대의 도구와 비교해보면 두 가지 면에서 차이가 있습니다. 먼저 고대의 도구는 ‘세는’ 행위와 관련이 있어요. 예를 들어 지금은 시장에서 곡식을 팔 때 저울에 올려 무게 단위로 팔지만, 얼마 전만 해도 한 되, 두 되씩 그릇으로 덜어서 줬어요. 고대에도 얼마만큼 잴 수 있는 도구로 몇 번인지 세어서 크기를 가늠했어요. 세는 게 중요하지 정확한 무게는 알 수 없었습니다. 그래서 고대 그리스에서는 그릇 크기를 속이는 사람이 없는지 감독하는 시장 감독관이 있었습니다.

또 고대의 도구는 현대와 달리 표준화되지 않았어요. 손가락 마디나 손목 마디 등을 이용해서 길이를 쟀는데, 문제는 사람마다 이 길이가 다 달랐지요. 근대에 와서 무게 1g, 길이 1cm, 온도 0℃ 같은 표준 단위가 정의됐어요.

수학자 : 도구나 각자만의 기준을 사용해서 눈앞에 있는 물체를 재왔네요. 그러면 언제부터 일반적인 도량이나 측정 말고, 학문으로서 기하학을 하기 시작했나요?

인문학자 : 기하학의 대표적인 책인 고대 그리스 수학자 에우클레이데스(유클리드, 기원전 4세기 추정)의 저서 <;원론>;부터 이야기해야 할 것 같아요. 이 책은 기원전 4, 3세기경까지 고대 그리스에 알려진 기하학적 지식을 연역적으로 정리하면서 도형의 크기를 어떻게 잴 것인가의 문제를 다뤄요. 에우클레이데스는 ‘서로 다른 두 도형이 있을 때 이 도형을 재는 공통의 단위가 있는가’라는 물음부터 시작합니다.

그렇지 않을 경우를 ‘통약 불가능한 관계’라고 하고, 유명한 예로 정사각형의 한 변의 길이와 대각선의 길이가 있습니다. 한 변의 길이가 1이라면, 대각선의 길이는 가 될 텐데 당시 무리수는 비로 표현할 수 없었습니다. 만약에 두 도형이 통약 가능해서 공통으로 재는 단위가 있다면 그다음 관심사는 두 도형 사이에서 길이의 관계, 넓이의 관계를 ‘비’로 나타내는 일이 됩니다.

우리는 비를 두 수 사이의 크기를 비교하기 위해서 쓰지만, <;원론>;에만 국한하면 크기를 정확하게 구할 수 없는 도형을 측정하기 위해 썼습니다. 측정해야 할 도형의 정확한 길이나 넓이를 구하는 대신에 크기를 잘 아는 도형과의 관계를 표현하는 방식을 택했다는 뜻입니다. 이러면 측정의 결과는 절대적인 수치가 아니라 두 도형 사이의 비로 나타나게 되지요.

수학자 입장에서 기하학은 어떤 학문인가요?

수학자 : 무언가 재는 행위는 기하학이 수학의 한 분야로 인정받기 훨씬 전부터 존재했어요. 어느 고대 문명을 보더라도 땅의 넓이를 재고 세금을 매기는 행위는 필요했으니까요. 그런 면에서 땅을 재는 행위 자체는 수학보다는 공학으로 볼 수 있는 것 같아요.

그렇지만 사칙연산과 수학이 다르듯, 단순히 길이, 넓이, 부피 등을 ‘재는 것’이 기하학의 전부는 아니에요. 기하학은 공간을 이해하고 공간 속 구조의 성질을 연구하는 학문이지요. 기하학 문제라고 하면 두 점 사이의 거리를 구하거나 2차원 평면 위에서 도형의 둘레 혹은 넓이를 구하는 문제가 떠오르잖아요.

그렇지만 애초에 거리와 공간을 어떻게 정의할지, 이 정의된 공간 속에 존재하는 도형의 성질을 어떻게 분석할지 알아야 거리를 ‘재고’, 넓이를 ‘재는’ 이차적 행동을 할 수 있겠지요. 그런 의미에서 기하학은 ‘재는’ 학문보다는 ‘잴 수 있게 하는’ 학문에 더 가깝다고 생각합니다.

두 번째 질문 기하학은 어떻게 발전해 나갔을까?

인문학자 : 대상을 잴 수 있게 하는 학문인 기하학은 어떤 발전 과정을 거쳤나요?

수학자 : 교수님께서 앞서 인류가 무엇을 잴 때 도구를 이용해 세었다가 점차 정확하게 측정했다고 말씀해주셨는데요. 기하학의 대상은 점점 더 추상화됐어요. 

좌표평면의 도입 이후에 기하학이 어떻게 변했는지를 예로 들어볼게요. 원은 한 점으로부터 같은 거리에 있는 모든 점의 집합이에요. 이때 이 원의 반지름을 r이라고 하면, 이를 x² + y² = r²이라는 식으로 나타낼 수 있어요. 이 식의 해를 모아놓은 집합을 좌표평면에 표현하면 원이 그려지지요.

이러한 추상화 과정을 통해서 현실에 존재할 수 없는 도형도 식으로 나타낼 수 있어요. 2차원의 원, 3차원의 구를 넘어 임의의 n차원 도형도 식으로 나타내 길이, 넓이, 부피를 ‘잴 수’ 있게 된 거지요. 기하학 덕분에 우리가 다룰 수 있는 도형의 범위가 무한하게 늘어난 겁니다.

인문학자 : 말씀을 듣고 보니 인류에게 잰다는 욕구가 어마어마한 것 같아요. 우리가 쉽게 잴 수 있는 것부터 시작해서 재기가 굉장히 어려운 어떤 대상까지 확장했으니까요. 기하학 발전의 역사를 볼 때 두 가지 차원에서의 확장을 이야기할 수 있어요.

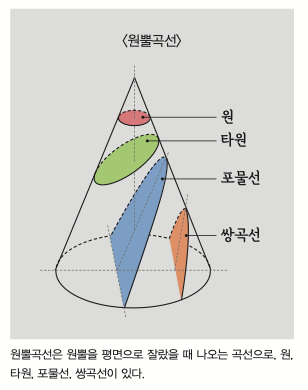
첫째는 자연 세계에서 발견할 수 있는 대상을 재는 행위에서 시작해서 우리가 창조하거나 추상화한 대상까지도 재는 거예요. 예를 들면 원뿔곡선이 있지요. 인류는 자연 세계에서 흔히 보는 곡선만 연구한 것이 아니라, 원뿔을 잘라서 원, 타원, 포물선, 쌍곡선 등의 곡선을 만들었습니다. 점점 더 복잡한 곡선을 가정해서 재보거나 기하학적으로 표현하는 단계까지 나아갔다는 점에서 의미가 있지요.

또 다른 차원의 확장은 멈추어 있던 도형에서 움직임을 반영한 도형까지 나아갔어요. 천문학에서는 기하학을 이용해 행성, 별 등의 움직임과 위치를 연구했고, 물리학에서는 입자의 움직임을 탐구했지요.

이 모든 확장의 끝은 독일 수학자 고트프리트 라이프니츠(1646~1716)의 사례로 이야기할 수 있습니다. 라이프니츠는 기하학에서 관심을 갖는 대상을 도형에 그치지 않고 어떤 공간 상에 놓인 도형의 위치로 넓혔지요.

결국 우리가 어떤 대상을 수학적으로 탐구할 때 ‘추상화’가 핵심이라고 할 수 있습니다. 그렇다면 기하학에서 추상적인 이해가 필요한 이유는 뭘까요?

수학자 : 굉장히 예리한 질문을 해주셨는데요. 모든 수학이 그렇듯, 추상적인 이해는 우리의 직관 혹은 인간이라는 생물의 한계를 뛰어넘게 해주기 때문에 중요하다고 생각해요. 때론 직관보다 더 고차원적인 이해가 필요하니까요.

예를 들면 어렸을 때 같은 모양끼리 모아보는 활동을 해본 적이 있을 거예요. 그러면 축구공, 야구공, 배구공, 농구공을 한 데에 모으지요. 각자가 크기는 다르지만, 우리는 모두 동그란 구 모양의 공이라는 걸 이해하고 있어요.

이렇게 단순히 길이나 크기 같은 직관적인 수치 비교를 넘어 추상적인 물체들의 성질을 연구하기 시작한 분야 중 하나가 ‘위상수학’이에요. 위상수학에서 흔히 도넛과 머그잔이 위상적으로 같다고 이야기해요. 두 물체 모두 구멍이 ‘하나’이므로, 찰흙을 변형시키듯 연속적으로 도넛을 줄이고 늘리고 하다 보면 머그잔을 만들 수 있기 때문이에요. 이렇게 어떤 물체의 구멍 개수를 ‘재는’ 게 중요해집니다. 이것도 이번 주제인 ‘재는’ 문제인 셈이지요. 

직관을 넘어서는 추상에 대한 이해는 어떻게 보면 수학의 발전을 넘어 인류 지성사의 발전과 같이한 것 같아요. 추상적인 기하학의 발전은 우리가 우주를 물리적으로 이해할 수 있게 도와주고, 실용적인 기술 발전의 기초가 됩니다. 추상적 이해를 가능하게 한 수학의 놀라움이라고도 생각합니다.

이번 시간에는 기하학의 재다에 대해서 생각해봤습니다. 

다음 시간에는 ‘왜 유클리드 기하학이 2000년 동안 서구 문명을 지배했을까?’를 주제로 이야기를 나눠보겠습니다.