d라이브러리

19세기 말 영국의 한 펍.

“저는 자유의지와 신의 전능이 양립할 수 없다고 생각해요. 이토록 모순이 많은 종교보다는 수학에서 확실한 앎의 토대를 찾을 수 있으리라 여겨서 수학과에 진학했어요. 이런, 말이 너무 길어졌네요.”

“버트런드, 너같은 후배를 만나서 얼마나 기쁜지 모르겠어! *화이트헤드 교수님이 너를 만나 보라고 적극 권유하신 이유가 있었구나.”

“전 지금까지 제가 이상한 아이인 줄 알았어요. 이런 이야기를 진지하게 들어주는 사람이 있다니 믿을 수 없어요.”

“당연히 있지, 아무렴. 여기는 케임브리지대야! 이곳에 입학한 것을 진심으로 환영해. 버트런드, 혹시 저녁에 시간이 되니? 괜찮으면 우리 ‘더 소사이어티(The Society)’ 모임에 가지 않을래? 다들 너와 친구가 되고 싶어 할 거야.”

“무,  물론이죠!”

나를 지지하는 사람

2023년 영국의 한 펍.

“정담, 그런데 넌 참 신기하다. 어쩌다가 대학에서 수학과 철학을 함께 공부하고 있는 거야? 둘이 완전 동떨어진 분야 아닌가?”

“음, 그렇지 않아. 고대 그리스 시절부터 철학자들은 진리를 찾고자 했어. 하지만 철학자들의 체면이 구겨질 정도로 일찍이 진리를 발견한 사람들이 있어. 수학자들이야. 생각해봐. 과학 이론은 시간이 지나면 틀린 것으로 판명되는 경우가 있어. 철학은 말할 것도 없고. 그런데 수학은 그렇지 않아. 수학의 정리는 의심할 수 없어. 언제 어디에서나 절대적으로 참이야. 인류가 일군 지식 중 가장 추상적이고 난해한 동시에, 가장 정확하고 우아하다고 생각해. 수학은 진리에 다가서기 위한 인류의 도전 중 가장 성공적이야.”

“그래서?”

“진리에 목숨을 건 수많은 철학자는 수학을 동경했어. 수학의 원리를 파헤치면 진리의 열쇠를 거머쥘 수 있으리라고 기대한 거지. 프랑스 철학자이자 수학자 르네 데카르트가 그랬고, 네덜란드 철학자 바뤼흐 스피노자가 그랬고, 버트런드 러셀이 그랬어. 물론 진리에 도달하기까지 헤쳐나가야 할 역경은 한참 남았어. 하지만 나는 2000년 동안 이어져 온 수학자, 철학자의 노력에 조금이나마 기여하고 싶어. 이런, 말이 너무 길어졌다.”

“음네 말을 완벽하게 이해하지는 못 했어. 하지만 네가 멋진 도전을 하고 있다는 건 분명히 알겠어. 너의 도전이 의미 있는 성과를 거두길!”

러셀이 있던 그곳 영국

안녕하세요 여러분, 저는 영국에 교환학생으로 와 있습니다. 그동안 정말 많은 일이 있었어요. 예쁜 캠퍼스를 산책하고, 기숙사 앞 고풍스러운 정원에서 평화로운 시간을 보냈습니다.

공부는 정말 재밌게 하고 있습니다. 이토록 다양한 책을 읽어보는 것도 오랜만이에요. 한국으로 돌아가면 어서 친구들에게 영국에서 배운 흥미로운 지식들을 풀어내보고 싶어요.

19세기 영국에서 러셀도 대학에서 마음 맞는 친구를 만나 학문의 재미에 푹 빠졌습니다. 청소년 시절, 주변 형들의 놀림과 종교적 회의심으로 인한 우울감에 시달렸던 모습과 딴판이지요. 러셀의 입학 면접을 담당한 화이트헤드 교수가 러셀의 총명함을 알아보고는 제자들에게 그를 만나 보라고 조언했습니다. 케임브리지대의 선배들은 러셀과의 만남이 인상깊었고 그를 더 소사이어티(The Society)라는 비밀 동아리에 초대했습니다.

'

학술적 토의가 주요 활동이었던 이 동아리에서는 모든 회원이 아무런 금기나 억압 없이 자유롭게 주장을 펼칠 수 있었습니다. 러셀은 이 동아리에서 평생지기를 사귀었을 뿐 아니라 엄청난 사유의 성장을 겪었다고 회고합니다. 이 시기를 거치며 러셀은 수줍고 우울했던 소년에서 쾌활하고 호기심 넘치는 청년으로 성장했습니다.

도전의식을 불러일으킨 미적분학

러셀은 케임브리지대 수학과를 7등으로 졸업하는 뛰어난 성과를 거둡니다. 그럼에도 러셀은 대학에서 가르치는 수학의 실태를 마주하고는 실망을 금치 못했습니다. 특히 그를 경악하게 만든 것은 ‘미적분학’이었습니다.

미적분학의 대표 개념인 접선의 기울기를 구하는 과정을 예시로 러셀이 어떤 부분에서 실망했는지 볼게요. 아래의 곡선은 y = x²입니다. 이 곡선과 (1, 1)에서 접하는 직선은 다음과 같습니다

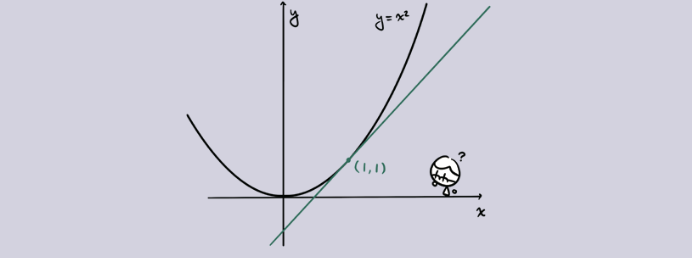
이 직선의 기울기를 구하고 싶다면 어떻게 해야 할까요? 만약 여러분이 러셀 시절에 수학을 공부했다면 이렇게 배웠을 겁니다. 접선은 곡선과 한 점에서 만나는 직선이지만, 잠시 접선을 ‘곡선 위의 아주 살짝만 떨어진 두 점을 지나는 직선’이라고 생각해봅시다. 두 점의 간격을 ε(엡실론)으로 나타내면 다음과 같습니다.

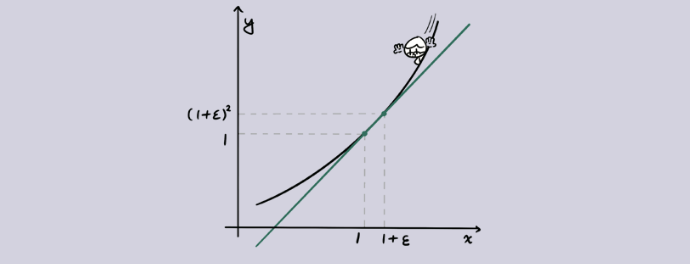
이 경우 초록색 직선의 기울기는 쉽게 구할 수 있습니다.

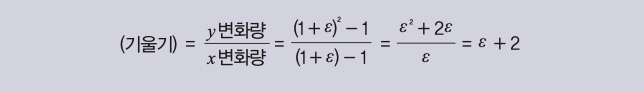
그런데 아까 전에 두 점이 아주 살짝만 떨어져 있다고 했던 것, 기억나나요? 두 점이 아주 살짝만 떨어져 있다면 ε은 0이나 다름이 없겠죠.  따라서 ε = 0으로 두면, 곡선의 기울기는 2라는 답을 얻습니다.

혹시 여러분의 반응이 ‘띠용?’이라면 정상입니다. 방금의 논증은 상당히 의심스럽습니다. 정말로 ε = 0이라면 두 점은 살짝 떨어져 있기는커녕 아예 동일한 점일 뿐더러, 기울기 식의 분모와 분자가 모두 0이 되는 셈이니 수학적으로 말이 안 됩니다. 이에 난처함을 느낀 수학자들은 ε을 ‘0은 아니지만 0에 무한히 가까운 값’이라는 의미에서 ‘무한소’라고 불렀습니다.

물론 이름을 새로 붙인다고 해서 미적분학의 본질적인 모순이 해결될 리는 없습니다. 그러나 모순이 있을지언정 미적분학은 물리학과 공학에서 매우 성공적인 결과를 이룩했습니다. 이에 수학계의 상당 인재들이 ‘입 다물고 계산이나 하자’는 사고방식에 사로잡혔어요.

러셀은 이대로 가다가는 수학의 석탑이 한순간에 무너지고 말 것이라고 생각했습니다. 이미 청소년기에 자신의 신념 체계가 무너지는 것을 경험한 러셀은 수학에서도 동일한 일이 일어나기를 원치 않았습니다. 케임브리지대를 졸업할 즈음 러셀은 수학의 토대를 확고히 다지는 작업의 필요성을 절감했습니다.

다행히도 수학의 위기를 직감한 사람은 러셀만이 아니었습니다. 러셀의 기숙사 건너편에서 화이트헤드 교수가 새로운 논리학을 위한 연구에 착수하고 있었습니다.

✲글쓴이 소개

최정담. 수학 베스트셀러 <;발칙한 수학책>;의 저자 최정담은 수학 대중화에 관심이 많고, 수학과 철학을 공부하는 KAIST 수리과학과 학생입니다. 영국의 수학자이자 철학자인 버트런드 러셀을 좋아해 이번 연재를 통해 러셀의 생애를 소개합니다.