d라이브러리

원숭이에게 노트북을 주고 키보드를 마음대로 두드리라고 하면 어떤 일이 벌어질까? lqnceyeioslowdnlvnlsharkwejad처럼 알 수 없는 알파벳이 연이어 나타날 것이다. 그런데 자세히 살펴보니 ‘shark’처럼 아는 단어도 있다. 설마 키보드를 막 두들기다 보면 책 한 권도 쓸 수 있는 건 아닐까?

18~19세기 유럽 사람들도 무한히 많은 시간 동안 타자기를 무작위로 치면 읽을 수 있는 문장이 만들어질지도 모른다고 생각했다. 1782년 조너선 스위너프가 출간한 <;걸리버 여행기>;에 이와 비슷한 상황이 나오는데, 그럴듯해 보였기 때문이다. 소설에선 신비로운 교수가 학생들을 시켜 인쇄 기계로 무작위한 문자열을 찍어 내 그 결과를 모아 과학 지식의 목록을 작성한다. 

이후 이런 생각은 프랑스 수학자 에밀 보렐에 의해 원숭이가 무한히 오랜 시간 동안 아무렇게나 타자기를 두드린 결과, 완벽한 책을 완성했다는 이야기로 바뀐다. 그 당시 프랑스 수학자 사이에선 <;걸리버 여행기>; 속 이야기가 실제로 가능한지 수학적으로 증명하는 것이 유행이었다. 보렐도 그중 한 사람이었는데, 그는 원숭이를 도입해 이를 증명했다.

보렐은 일어나기 힘든 일이라는 것을 강조하기 위해 원숭이가 타자기를 친다고 가정했다. 그리고 자신이 고안한 ‘두 번째 보렐-칸텔리 보조정리’를 이용해 원숭이가 무한히 많은 시간 동안 무작위로 타자기를 치면 완벽한 책을 칠 가능성이 ‘거의 확실하다’라는 것을 증명하고, ‘무한 원숭이 정리’라고 이름 붙였다. 어느 순간 무한 원숭이 정리에 등장하는 ‘완벽한 책’은 셰익스피어의 희곡 또는 <;햄릿>;으로 바뀌어 소개되고 있다. 

원숭이 떼가 바나나를 칠 확률은 100%

‘banana’를 한 번에 입력하려면 원숭이 몇 마리가 필요할까? 무한 원숭이 정리에서는 원숭이 한 마리에게 무한히 많은 시간을 준다. 따라서 현실에서 이를 확인하기란 어렵다. 그래서 이후 수학자들은 원숭이의 수를 무한히 많은 것으로 바꿔 무한 원숭이 정리를 따져봤다. 사실 이것도 쉬운 일은 아니지만, 시간이 무한히 많은 것보다는 원숭이의 수가 많은 것이 좀 더 현실적이라고 여긴 것이다. 

여기서는 원숭이가 무한히 많을 때로 가정하고, 쉽게 계산하기 위해서 원숭이가 ‘banana’를 칠 확률을 구해보자. 이때 타자기는 50개 키로 이뤄져 있다. 

한 마리의 원숭이가 타자기의 키를 1번 눌러 ‘banana’의 ‘b’를 칠 확률은 50개 중에 1개의 키를 입력하는 것이므로 1/50이다. 두 번째에 ‘a’를 칠 확률은 1/50 × 1/50이 된다. 두 가지 이상의 사건이 동시에 일어날 경우에는 각각의 사건이 일어날 확률을 곱한 것과 같기 때문이다. 

마찬가지 방법으로 나머지 문자들을 연속으로 쳐서 ‘banana’라는 단어를 입력할 확률을 구하면 이 된다. 반대로 원숭이가 연속해서 6번 타자기를 쳤을 때 ‘banana’를 치지 못할 확률은 1 - 1/(50⁶)이다. 

그렇다면 n마리의 원숭이가 연속해서 6번 키를 입력했을 때 ‘banana’를 치지 못할 확률은 얼마일까? 1 - 1/(50⁶)을 n번 곱한 것과 같으므로 {1 - 1/(50⁶)}ⁿ이다. 이때 n이 100만이라면 이 값은 약 0.9999다. 즉 100만 마리의 원숭이가 6번의 입력으로 ‘banana’를 입력하지 못할 확률이 99.99%라는 뜻이다. 

그런데 n이 100억이 되면 그 확률은 약 53%가 되고, 1000억이 되면 0.17%까지 떨어진다. 결국 원숭이 수가 무한히 많으면 목표 단어를 입력하지 못할 확률은 0에 가까워진다는 의미다. 즉, 무한히 많은 원숭이 떼가 목표 단어를 입력할 확률은 거의 100%가 된다.

원숭이들이 완벽한 책을 쓸 일은 매우 희박하지만, 확률적으로 충분히 발생할 수도 있는 사건이라는 뜻이다. 

무한 원숭이 정리, 실험 결과는?

2002년에는 영국 플리머스 대학 미디어랩 예술과정에서 실제 원숭이 6마리를 대상으로 무한 원숭이 정리를 실험해 화제가 됐다. 당시 영국의 웹사이트와 라디오에서는 이 연구를 실시간 중계했다.

그런데 한 달 동안 원숭이가 만들어 낸 결과물은 알파벳 S가 대부분인 종이 5장에 불과했다. 실험장은 원숭이 배설물로 가득했고, 원숭이들이 키보드를 부수기도 해 더 이상의 실험이 불가능할 정도였다. 이 프로젝트에 참여했던 에이미 플라우맨 동물학 박사는 수학적 이론과 현실은 차이가 크다고 밝혔다. 

한편 2003년 미국 프로그램 개발자들은 ‘자바 애플릿’이라는 컴퓨터 프로그램을 이용해 무한 원숭이 정리를 모의실험했다. 일명 ‘원숭이 셰익스피어 시뮬레이터 프로젝트’다. 

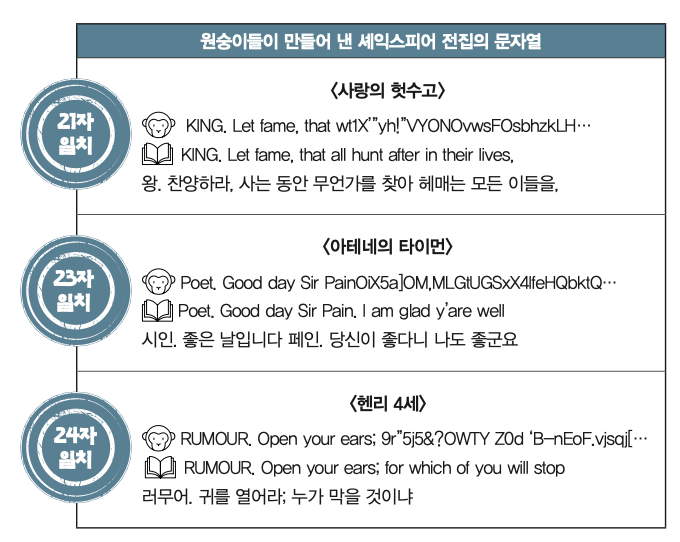
7월 1일 원숭이 100마리를 시작으로, 며칠마다 원숭이 수를 2배로 늘리면서 2007년까지 진행했다. 이 기간에 원숭이들은 한 장에 2000자가 들어가는 종이를 10³⁵장이나 만들어 냈다. 

개발자들은 매일 나온 산출물 중에서 셰익스피어 전집의 문자열과 일치하는 가장 긴 문장을 공개했다. 일반적으로 문자열의 길이가 18자 또는 19자였고, 시간이 지남에 따라 조금씩 문자열의 길이가 길어졌다. 프로젝트 기간 발견한 가장 긴 문자열은 2005년 1월 나온 24자인데, 이때까지 원숭이들이 작업한 글자 수가 무려  2,737,850 × 10³³에 이른다.