d라이브러리

수학자 : 대수(代數)라는 단어를 보면 대명사(代名詞) 할 때의 대(代)처럼 대신한다는 의미가 있어요. 그런 점에서 보면 단순히 x라고 표기된 것이 의미 있다기보다는 어떤 대상을 기호로 대신 나타내는 기호화가 이뤄진 게 수학사에서는 큰 의미가 있는 것 같아요.

예를 들어서 5라는 숫자가 있으면 사과 5개, 사람 5명, 5시간 이렇게 모두 5라는 수로 묶이잖아요. 다섯의 의미를 숫자 5로 기호화 하니 쉽게 표현하고 소통할 수 있는 거지요. 또 다른 예로 삼각형의 넓이를 구한다고 하면 밑변 × 높이 × 1/2 이잖아요. 이렇게 밑변과 높이라는 단어가 있고 그 둘을 곱해서 2로 나누면 삼각형의 넓이가 나온다고 설명할 수 있어요. 우리가 대화할 때 늘 단어 하나하나의 의미부터 설명하기 시작하면 더 정확할 수는 있지만, 장황하겠지요.

그런데 수학이 기호화 되면서 배경 지식과 상관없이 우리는 x와 y라는 숫자가 있고 2분의 1이라는 개념을 알고 있으면 (x×y)/2로 삼각형의 넓이를 나타낼 수 있어요. 그렇게 되면 어떤 맥락 없이도 원하는 설명을 간단한 수식으로 표현할 수 있어요.

방정식에서 x의 사용, 즉 기호화라는 게 수학의 개념화 혹은 추상화 같은 데에서 굉장히 큰 발전을 이뤄냈다고 생각해요. 그리고 반대로 얘기하면 x라는 기호가 수학을 발전시켰다기보다는 수학이 그만큼 x라는 기호를 수용해서 식을 나타낼 수 있을 정도로 발전했다고 역으로 생각할 수 있습니다.

인문학자 : 특히 현대 수학자 입장에서는 더 복잡한 상황에서도 기호를 씀으로써 내용을 더 명료하게 정리할 수 있고 다른 사람에게 전달하는 데도 도움이 됩니다.

그런데 학생들은 기호화의 장점 못지않게 단점도 많이 느끼지 않을까 생각합니다. 여러분이 수학 교과서에서 많이 보는 ‘문장제 문제’가 원래는 날것 그대로의 방정식 문제라고 할 수 있지요. 우리는 그 문장제 문제를 기호로 바꿔서 풀게 되는데, 사실은 기호를 쓰지 않고 원래 그대로의 대수적 상황을 접근하고 또 그걸 기하적으로도 생각해보는 과정이 주는 굉장한 이점이 있어요. 우리는 단순히 (x + y)² = x² + 2xy + y² 이라는 공식을 외우는데 그걸 그렇게 기호화하지 않고 (x + y)² 을 도형으로 표현하는 등 실체 그대로 접근을 했을 때 느껴지는, 손에 만져질 것 같은 흥미진진한 수학이 있거든요. 고대에는 그런 접근이 많이 보였지요. 

하지만 수학이 점점 고도로 추상화 되고 있어서 이제 예전 방식으로 돌아가기는 힘들 거예요. 현대 수학자들에게 너무 중요하고 필요한 일이지만, 조금만 다른 시각으로 보면 수학을 배우는 학생들에게 기호화가 꼭 도움이 되는 것인가를 한번 반성적으로 생각해볼 필요가 있어요.

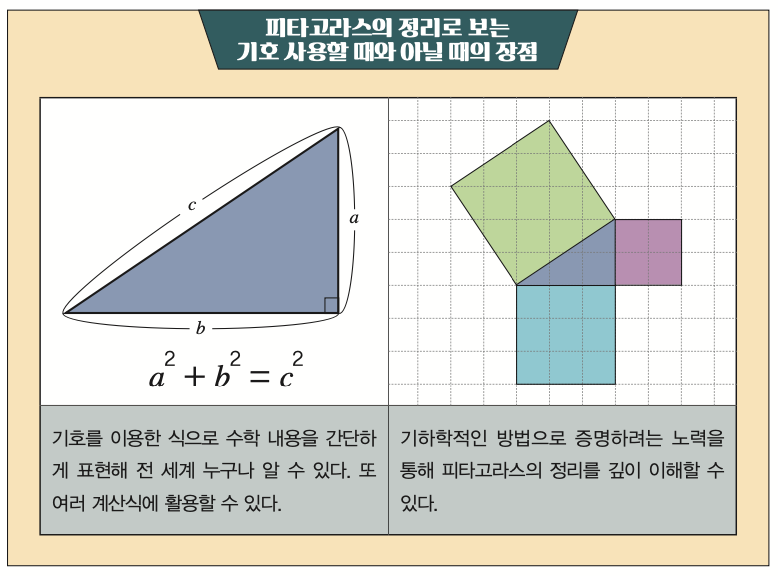
수학자 : 교수님 이야기에 굉장히 동의합니다. 왜냐하면 피타고라스의 정리에서도 a² + b² = c²이 되는 직각삼각형이 있다는 것을 공식이 아닌 기하학적으로 알 수 있거든요. 기하학적인 증명들이 이삼백 가지나 되지요. 모래를 담아서 진짜 넓이를 구해 볼 수도 있고요. 

어떤 일이 몇 번 벌어졌을 때 다음에는 어떤 일이 벌어질까 하는 규칙을 찾거나 예측하는 것도 어떻게 보면 수학이 하는 일이고 나아가서 인류의 본성 중에 하나라고 생각합니다. 

학생들이 1, 2, 3을 거쳐서 n으로 이렇게 가는구나를 눈으로 보게 되면 수학을 재미있고 즐겁게 배울 수 있는데, 그 과정을 건너뛰고 n을 배운 다음 n에 1을 대입해 맞는지 확인하려고 하면 진짜로 수학이 와닿지 않고 건조하다는 생각이 들 수도 있을 것 같아요. 그래서 수학에서 손으로 만져보는 혹은 눈으로 보는 것이 중요하다고 생각해요. 실제로 현대 수학자들도 ‘수학은 손을 더럽혀보면서 하는 과목이다’라는 말을 많이 하거든요. 그렇게 수학에 접근하면 조금 더 재미있게 수학을 공부할 수 있지 않을까 하는 생각이 듭니다.