d라이브러리

 ● 달콤한 첫사랑, 수학의 배신 ●

러셀에게 행복을 준 또 다른 것은 수학이었습니다. 러셀은 열한 살 때 형에게 유클리드 기하학을 배우기 시작했는데요. 훗날 러셀은 그 순간을 다음과 같이 회고합니다.

수학이 첫사랑과도 같은 경험이었다니 잘 와닿지가 않죠? 하지만 수학의 원리를 곰곰이 생각해보면 얼마나 우아하고 매력 있는지가 드러납니다.

한 가지 예시로 삼각형의 세 내각의 합을 구하는 문제를 생각해봅시다. 가장 직관적인 방법은 여러 가지 모양의 삼각형을 그려본 후, 각도기로 세 내각의 합을 구해보는 것입니다. 이 과정을 반복하면 우리는 매우 많은 경우 삼각형 세 내각의 합이 180°임을 발견할 수 있습니다. 그러나 모든 삼각형의 세 내각의 합이 180°라고 확실히 말할 수는 없을 뿐더러, 왜 그래야 하는지 이해할 수 없습니다.

대신 고대 그리스 수학자 에우클레이데스(유클리드)의 <;원론>;에서 아래의 그림을 소개합니다. 러셀이 큰 감명을 받은 논증이기도 합니다. 

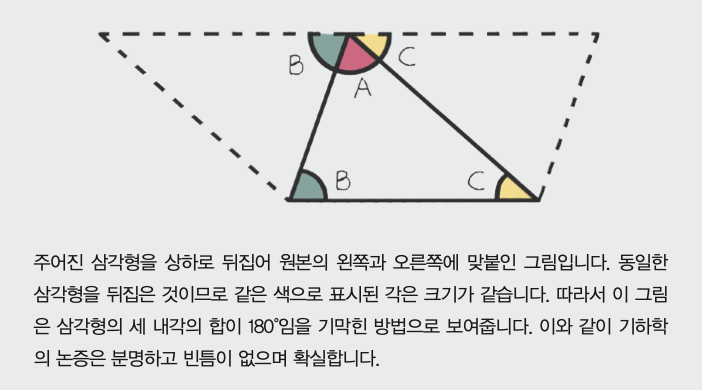
이런 우아한 기하학의 정원이 러셀의 눈 앞으로 펼쳐졌습니다. 펨브로크 로지의 넓디넓은 정원 못지않게 아름다운 그곳에서 러셀은 기하학 탐구에 푹 빠졌습니다. 그러나 얼마 후 문제가 생겼습니다. 문제의 발단은 ‘평행선 공준’이었습니다.

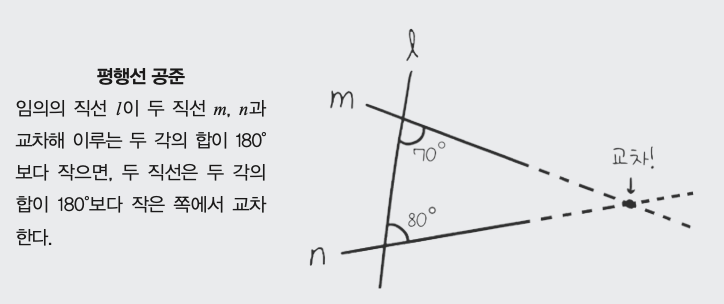
이 공준은 ‘닮은 두 삼각형이 존재한다’, ‘모든 삼각형은 외접원을 가진다’ 등의 매우 중요한 정리를 증명하는 데 필요하기 때문에, 당연히 러셀은 형에게 평행선 공준을 어떻게 증명하는지 물어봤습니다. 그러나 형의 대답은 뜻밖이었습니다.

“평행선 공준은 증명할 수 없어.”

제아무리 기하학이 뛰어나 봤자 인간이 만든 학문이기 때문에, 몇 가지 기본적인 가정은 필요하다는 설명이 뒤따랐습니다. 덧붙여 수천 년 동안 유수한 수학자들이 평행선 공준을 증명하려고 시도했지만 모두 실패했다는 이야기도 언급했지요.

이 말을 들은 러셀은 충격에 빠졌습니다. 기하학의 낙원 위로 해일이 덮쳤고, 러셀은 파도에 떠밀려 허우적댔습니다. 기하학조차 우리에게 확실한 앎을 주지 못한다면 도대체 확실한 앎이란 가능한 것일까요? 평행선 공준조차 증명하지 못하는 인간이 어떻게 신의 존재나 삶의 가치나 선과 악에 대해서 논할 수 있다는 것일까요?

어느덧 러셀은 마냥 행복했던 소년기를 지나, 실존적 고민으로 점철될 사춘기로 돌입하고 있었습니다.