독일의 수학자이자 논리학자인 고틀로프 프레게는 ‘집합’을 이용해서 자연수로부터 수학의 개념을 모두 확장할 수 있다는 ‘자연수 이론’을 증명하려고 했습니다. 그러나 프레게의 이런 생각은 영국 수학자 버트런드 러셀의 편지 한 장으로 무너졌어요.
오늘은 편지 내용의 핵심인 ‘러셀의 역설’에 대해 알아볼게요.
♥ 당연한 말인데, 당연하지 않다?
논리학이 수학의 밑바탕이라고 보는 프레게의 논리주의 프로그램은 다음 원리에 기반합니다. 바로 ‘두 집합의 각 원소를 일대일로 대응할 수 있다면, 두 집합의 크기는 같다’입니다. 18세기 영국의 철학자 데이비드 흄의 이름을 따서 ‘흄의 원리’라고 부르지요.
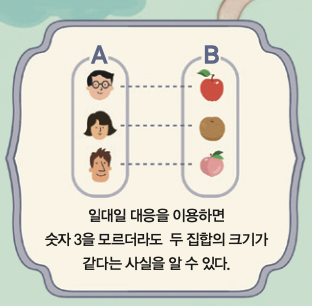
흄의 원리는 논리학의 기호들로 아래와 같이 기술할 수 있습니다. 이 식은 프레게가 저서 <;산술의 기본 법칙>;에서 소개한 다섯 번째 기본 원리여서 ‘프레게의 제5공리’라고도 부릅니다. 공리란 증명이 필요하지 않은 수학의 기반을 가리키는 말이에요.

다행히 여러분이 위 식을 이해할 필요는 없답니다. 대신 여러분이 알아야 할 점은 프레게의 제5공리로부터 아래의 사실이 유도된다는 사실이에요.

음, 근데 이것도 무슨 말인지 바로 알기 어렵지요. 조금 쉽게 풀어서 설명해 볼게요! 예를 들어 P(x)라는 명제가 주어졌다고 합시다. P(x)는 ‘4보다 작은 자연수’라고 할게요. 그러면 P(x)를 만족하는 대상들로 이뤄진 집합 {1, 2, 3}이 항상 존재한다고 볼 수 있겠죠? 즉 어떤 명제를 만족하는 대상들로 이뤄진 집합을 항상 만들 수 있다는 말이에요. 어떻게 보면 너무나 당연한 내용을 주장하고 있는 것 같네요. 그래서 프레게도 문제가 있을 거라고는 생각하지 않았죠. 그러나 여기엔 역설의 씨앗이 도사리고 있었답니다.
♣ 자기 자신을 포함하지 않는 집합
앞의 주장에 따르면 어떠한 명제도 집합을 구성하는 데 쓰일 수 있습니다. 이것이 참인지 확인하기 위해 러셀은 다음과 같은 명제를 생각해 냈습니다.

이게 무슨 수수께끼 같은 말일까요? 차근차근 설명해 볼게요. 집합은 크게 두 가지 부류로 나눌 수 있습니다. 첫 번째 부류는 자기 자신을 포함하는 집합입니다. ‘모든 집합의 집합’, ‘정수가 아닌 모든 것의 집합’, ‘고체가 아닌 것의 집합’이 그 예지요. 집합 그 자체가 ‘집합’, ‘정수가 아닌 모든 것’이며 ‘고체가 아닌 것’이기 때문에 자기 자신을 포함하죠.
두 번째 부류의 집합은 자기 자신을 포함하지 않는 집합입니다. ‘모든 짝수의 집합’, ‘모든 정수의 집합’, ‘모든 자음의 집합’이 이에 해당합니다. 집합 그 자체가 ‘짝수’, ‘정수’, ‘자음’은 아니기 때문에 자기 자신을 포함하지 않아요. 사실 대부분이 이 경우에 해당합니다.
우리는 R(x)를 만족하는 대상들로 이뤄진 집합을 구성할 수 있습니다. 즉 자기 자신을 포함하지 않는 집합인 원소들로 이뤄진 집합이에요. 이 집합을 ‘러셀의 집합(Russell’s Set)’, 줄여서 ‘RS’라고 부르겠습니다. 이제 우리는 러셀의 역설을 이해할 준비가 다 되었습니다.

♠ RS로 밝힌 러셀의 역설
먼저 RS가 자기 자신을 포함한다고 가정해 봅시다(가정1). 즉 RS는 RS의 원소입니다. 그런데 RS의 모든 원소는 자기 자신을 포함하지 않아야 하므로, RS는 자기 자신을 포함할 수 없습니다. 이건 가정1을 위배해요. 따라서 귀류법에 의해 RS는 자기 자신을 포함하지 않아야 합니다. 귀류법이란 어떤 명제가 참임을 증명할 때 그 명제의 결론을 부정을 가정하고 모순이 생김을 보여 원래 명제가 참임을 증명하는 방법이에요.
그렇다면 RS가 자기 자신을 포함하지 않는다고 가정해 볼게요(가정2). RS에 포함되지 않는 모든 원소들은 자기 자신을 포함하는 원소여야 하겠지요. 따라서 RS는 자기 자신을 포함하는 집합이에요. 하지만 이 결론 또한 가정2를 위배합니다. 따라서 귀류법에 의해 RS는 자기 자신을 포함해야 합니다!
이처럼 ‘RS는 자기 자신을 포함한다’는 가정과 ‘RS는 자기 자신을 포함하지 않는다’는 가정이 둘 다 모순되는 명제입니다. 이런 러셀의 역설에 의해 집합으로 구성된 프레게의 수학 체계는 엉터리인 것으로 드러났지요.
◆ 러셀의 역설 그 이후
러셀의 역설로 인해 수학계는 떠들썩해졌습니다. 논리주의 프로그램에 적대감을 가졌던 프랑스 수학자 앙리 푸앵카레는 쾌재를 불렀지만, 집합론이 수학의 기반을 마련해줄 것이라 믿은 다비트 힐베르트, 주세페 페아노 등의 수학자들은 심각한 고민에 빠졌죠. 그중에서도 가장 큰 충격을 받은 사람은 단연 프레게입니다. 러셀의 편지를 받고 좌절한 프레게가 출판사에 자신의 서적 출판을 당장 중단할 것을 요구한 일화는 유명하죠.